强化学习导论_Example 6.5: Windy Grid-world
- 组会汇报时需要整理 《强化学习导论》第二版- Sutton一书中的例题代码,所以将理解过程记录了一下,并且巩固一遍python的基础知识。
- 书中页码:
P130, 对应Chapter 6: Temporal-Difference Learning
一、Problem:
1、Grid-world: 7x10 从起点(3,0)到达终点(3,7)
| 0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 (3,0) | (3, 7) | ||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6, 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2、Wind: 在中间区域,智能体执行完动作之后的状态的位置会被“风”再向上吹一点
| 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 1 | 0 |
|---|
3、Actions: up, down, left, right
4、不带折扣的分幕式任务,在到达目标前,每步会收到每步均为-1的收益。
二、Code:
使用 ϵ − \epsilon- ϵ−贪心的Sarsa算法: ϵ = 0.1 , α = 0.5 \epsilon=0.1, \alpha=0.5 ϵ=0.1,α=0.5, 对于所有的 s , a s,a s,a进行同样的初始化 Q ( s , a ) = 0 Q(s,a)=0 Q(s,a)=0。
1、导入库
#######################################################################
# Copyright (C) #
# 2016-2018 Shangtong Zhang([email protected]) #
# 2016 Kenta Shimada([email protected]) #
# Permission given to modify the code as long as you keep this #
# declaration at the top #
#######################################################################
import numpy as np
import matplotlib
matplotlib.use('TkAgg') #show fig
import matplotlib.pyplot as plt
numpy是使用C语言实现的一个数据计算库,它用来处理相同类型,固定长度的元素。使用numpy操作数据时,系统运行的速度比使用python代码快很多。numpy中还提供了很多的数据处理函数,例如傅里叶变化,矩阵操作,数据拟合等操作。numpy的官方网站是www.numpy.org
matplotlib是Python的一个绘图库,是Python中最常用的可视化工具之一,可以非常方便地创建2D图表和一些基本的3D图表。它以各种硬复制格式和跨平台的交互式环境生成出版质量级别的图形。通过Matplotlib,开发者可能仅需要几行代码,便可以生成绘图、直方图、功率谱、条形图、错误图、散点图等。默认情况下,matplotlib的backend使用的是agg,或template,此时是无法显示图片的,agg库不支持。关于后端库调整参见:https://blog.csdn.net/tanmx219/article/details/88074600.
matplotlib.pyplot:提供了一整套和Matlab相似的命令API,十分适合交互式地进行制图。而且也可以方便地将它作为绘图控件,嵌入GUI应用程序中。
2、初始化参数
# world height
WORLD_HEIGHT = 7
# world width
WORLD_WIDTH = 10
# wind strength for each column
WIND = [0, 0, 0, 1, 1, 1, 2, 2, 1, 0]
# possible actions
ACTION_UP = 0
ACTION_DOWN = 1
ACTION_LEFT = 2
ACTION_RIGHT = 3
# probability for exploration
EPSILON = 0.1
# Sarsa step size
ALPHA = 0.5
# reward for each step
REWARD = -1.0
START = [3, 0]
GOAL = [3, 7]
ACTIONS = [ACTION_UP, ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT]
Python列表 - 列表用 [ ] 标识,是 python 最通用的复合数据类型。
List(列表) 是 Python 中使用最频繁的数据类型。
列表可以完成大多数集合类的数据结构实现。它支持字符,数字,字符串甚至可以包含列表(即嵌套)。
列表中值的切割也可以用到变量 [头下标:尾下标] ,就可以截取相应的列表,从左到右索引默认 0 开始,从右到左索引默认 -1 开始,下标可以为空表示取到头或尾。

详见菜鸟教程-python 变量类型一节:https://www.runoob.com/python/python-variable-types.html
3、定义子函数def step(state, action): 输入每步的状态和行动后,根据所做的行动对当前状态进行更新。因为状态由坐标表示,分横纵坐标,所以state有两个数。这里子函数接收到state后赋值给i, j,后面调用的也是state[0]和state[1]。
def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
因为网格定义大小时是7x10,而在python中,索引是从0开始的,所以在进行上下左右移动操作时 ,需要保证下一步状态的更新不会超出网格世界,所以代码中,以向上为例 :max(i - 1 - WIND[j], 0)是垂直方向减一,并且减去此列风的影响,得到下一个格子,但是和0进行取max操作,防止超出第一行的边界。同理向右操作时 ,还需要看水平方向是不是超出了最后一列的边界,进行了取min操作。
4、执行一幕(episode)的操作
# play for an episode
def episode(q_value):
# track the total time steps in this episode
time = 0
# initialize state
state = START
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
action = np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# keep going until get to the goal state
while state != GOAL:
next_state = step(state, action)
if np.random.binomial(1, EPSILON) == 1:
next_action = np.random.choice(ACTIONS)
else:
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
# Sarsa update
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
state = next_state
action = next_action
time += 1
return time
主要过程是先设置当前state为出发点,然后通过$\epsilon-$贪心算法 进行action的选择:若以概率EPSILON随机产生的数刚好是1,则随机选取一个行动;若不是,则将此时state对应的q_value列表中对应的所有动作(上下左右)的对应价值都取出来赋值给values,然后取values中最大的值,其对应的action作为行动。然后判断当前的state是否为终点,若不是,则将当前(state,action)输入step()函数,返回下一时刻的状态即坐标,命名为 next_state, 得到状态后再使用 ϵ − \epsilon- ϵ−贪心算法选取行动。然后有了$ t$ 时刻的state和action,以及 t + 1 t+1 t+1 时刻的next_state和 next_action,以及已知到达终点前,每一步固定的reward=-1, 即已经有了五元组,所以通过Sarsa算法更新q_value。再进行state和action的更替,重复上述过程。
上述代码块中的函数解释如下:
np.random.binomial()是一个 二项式分布函数,具体见:https://blog.csdn.net/u014571489/article/details/102942933
#R = np.random.binomial(n,p,size)
#n:一次实验的样本数
#p:试验成功的概率
#size:试验的次数
#R:一个/列数字
np.random.choice()是从数组中随机抽取元素,具体见:https://blog.csdn.net/ImwaterP/article/details/96282230
例如:从数组、列表或元组中随机抽取。注意:不管是什么,它必须是一维的!
L = [1, 2, 3, 4, 5]#list列表
T = (2, 4, 6, 2)#tuple元组
A = np.array([4, 2, 1])#numpy,array数组,必须是一维的
A0 = np.arange(10).reshape(2, 5)#二维数组会报错
>>>np.random.choice(L, 5)
array([3, 5, 2, 1, 5])
>>>np.random.choice(T, 5)
array([2, 2, 2, 4, 2])
>>>np.random.choice(A, 5)
array([1, 4, 2, 2, 1])
>>>np.random.choice(A0, 5)#如果是二维数组,会报错
ValueError: 'a' must be 1-dimensional
enumerate()函数循环索引和元素,可同时获取索引和value,具体见:https://blog.csdn.net/fengdu78/article/details/104082179?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7Edefault-1.no_search_link
例如:如果我们想要列举一个列表,可以利用for循环并遍历每个项目的索引和值:
sports = ['soccer', 'basketball', 't` ennis']
for index, value in enumerate(sports):
print(f"The item's index is {index} and its value is '{value}'")
输出:
The item's index is 0 and its value is 'soccer'
The item's index is 1 and its value is 'basketball'
The item's index is 2 and its value is 'tennis'
4、画图
def figure_6_3():
q_value = np.zeros((WORLD_HEIGHT, WORLD_WIDTH, 4))
episode_limit = 500
steps = []
ep = 0
while ep < episode_limit:
steps.append(episode(q_value))
# time = episode(q_value)
# episodes.extend([ep] * time)
ep += 1
steps = np.add.accumulate(steps)
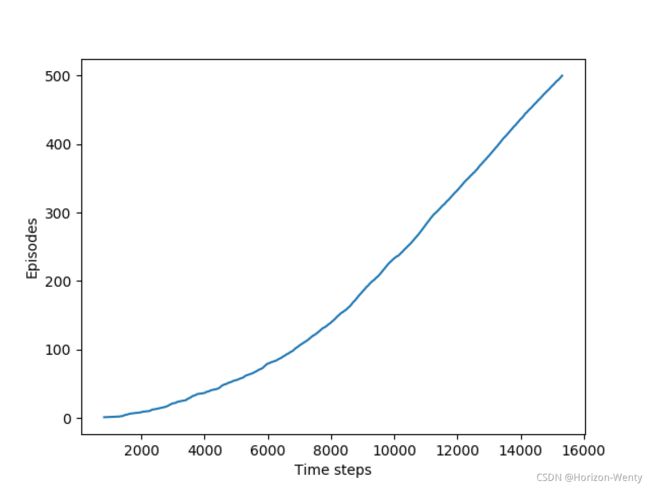
plt.plot(steps, np.arange(1, len(steps) + 1))
plt.xlabel('Time steps')
plt.ylabel('Episodes')
# plt.savefig('../images/figure_6_3.png')
# plt.close()
plt.show()
# display the optimal policy
optimal_policy = []
for i in range(0, WORLD_HEIGHT):
optimal_policy.append([])
for j in range(0, WORLD_WIDTH):
if [i, j] == GOAL:
optimal_policy[-1].append('G')
continue
bestAction = np.argmax(q_value[i, j, :])
if bestAction == ACTION_UP:
optimal_policy[-1].append('U')
elif bestAction == ACTION_DOWN:
optimal_policy[-1].append('D')
elif bestAction == ACTION_LEFT:
optimal_policy[-1].append('L')
elif bestAction == ACTION_RIGHT:
optimal_policy[-1].append('R')
print('Optimal policy is:')
for row in optimal_policy:
print(row)
print('Wind strength for each column:\n{}'.format([str(w) for w in WIND]))
上述代码块中的函数解释如下:
numpy.zeros(np.zeros)返回来一个给定形状和类型的用0填充的数组,具体参见: https://blog.csdn.net/qq_36621927/article/details/79763585
zeros(shape, dtype=float, order=‘C’)
shape:形状
dtype:数据类型,可选参数,默认numpy.float64
order:可选参数,c代表与c语言类似,行优先;F代表列优先
例如:
import numpy as np
print(np.zeros((2,5)))
结果为一个2行5列的矩阵:
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
append() 方法用于在列表末尾添加新的对象。语法为:list.append(obj), 参数是:obj -- 添加到列表末尾的对象, 返回值:该方法无返回值,但是会修改原来的列表。 具体参见:https://www.runoob.com/python/att-list-append.html
例如:
#!/usr/bin/python
aList = [123, 'xyz', 'zara', 'abc'];
aList.append( 2009 );
print "Updated List : ", aList;
以上实例输出结果如下:
Updated List : [123, 'xyz', 'zara', 'abc', 2009]
np.add.accumulate() 累加(每一个位置的元素和前面的所有元素加起来求和),返回的数组和输入的数组的shape相同,保存所有的中间计算结果。具体参见:
https://blog.csdn.net/weixin_43584807/article/details/103095888
https://blog.csdn.net/mingzhuo_126/article/details/81268438
例如:
>>> np.add.accumulate([1,2,3])
array([1, 3, 6])
>>> np.add.accumulate([[1,2,3],[4,5,6]], axis=1)
array([[ 1, 3, 6],
[ 4, 9, 15]])
np.arange()函数返回一个有终点和起点的固定步长的排列,如[1,2,3,4,5],起点是1,终点是6,步长为1。
参数个数情况: np.arange()函数分为一个参数,两个参数,三个参数三种情况
1)一个参数时,参数值为终点,起点取默认值0,步长取默认值1。
2)两个参数时,第一个参数为起点,第二个参数为终点,步长取默认值1。
3)三个参数时,第一个参数为起点,第二个参数为终点,第三个参数为步长。其中步长支持小数
例如:
#一个参数 默认起点0,步长为1 输出:[0 1 2]
a = np.arange(3)
#两个参数 默认步长为1 输出[3 4 5 6 7 8]
a = np.arange(3,9)
#三个参数 起点为0,终点为3,步长为0.1 输出[ 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9]
a = np.arange(0, 3, 0.1)
range ()函数的使用是这样的: range(start, stop[, step]),分别是起始、终止和步长。range(3)即:从0到3,不包含3,即0,1,2 具体见:https://blog.csdn.net/weixin_38705903/article/details/79238226 ,https://www.runoob.com/python3/python3-func-range.html
例如:range(1,3,2)即:从1到3,每次增加2,因为1+2=3,所以输出只有1。第三个数字2是代表步长。如果不设置,就是默认步长为1。
>>> for i in range(1,3,2):
print(i)
1
三、Results
Optimal policy is:
['U', 'D', 'R', 'R', 'D', 'R', 'R', 'R', 'R', 'D']
['R', 'R', 'R', 'D', 'U', 'D', 'R', 'R', 'U', 'D']
['R', 'R', 'R', 'R', 'R', 'R', 'D', 'U', 'D', 'D']
['U', 'R', 'U', 'R', 'R', 'R', 'U', 'G', 'R', 'D']
['D', 'D', 'D', 'R', 'U', 'R', 'U', 'D', 'L', 'L']
['L', 'R', 'R', 'R', 'R', 'U', 'U', 'D', 'D', 'D']
['R', 'D', 'R', 'R', 'U', 'U', 'U', 'U', 'U', 'L']
Wind strength for each column:
['0', '0', '0', '1', '1', '1', '2', '2', '1', '0']
Process finished with exit code 0