【控制】自适应控制,模型参考自适应控制,参考模型如何求取,有程序有图
| 目录 | 自适应控制的一点笔记和看法 |
|---|---|
| 1 | 【控制】自适应控制基本概念 |
| 2 | 【控制】自适应控制,对参考信号跟踪,对未知参数估计的小例子,带程序有结果图 |
| 3 | 【控制】自适应控制,模型参考自适应控制,公式推导,有程序有结果图 |
| 4 | 【控制】自适应控制,模型参考自适应控制,参考模型如何求取,有程序有图 |
文章目录
- 1 问题描述
-
- 1.1 被控对象
- 1.2 参考模型
- 1.3 跟踪控制器
- 2 参考模型的选择
- 3 实验验证
-
- 3.1 k 1 = − 5 , k 2 = 2 \red{k_1} = -5, \red{k_2} = 2 k1=−5,k2=2
- 3.2 k 1 = 5 , k 2 = − 2 \red{k_1} = 5, \red{k_2} = -2 k1=5,k2=−2
- 3.3 k 1 = − 5 , k 2 = − 2 \red{k_1} = -5, \red{k_2} = -2 k1=−5,k2=−2
- 3.4 k 1 = − 10 , k 2 = 2 \red{k_1} = -10, \red{k_2} = 2 k1=−10,k2=2
- 3.5 实验用程序
- 4 结论
1 问题描述
在之前的文章【控制】自适应控制,模型参考自适应控制,公式推导,有程序有结果图中,我们就被控系统如何跟随参考模型的问题进行了分析,设计了跟踪控制器 u u u。当被控系统中参数 a , b a,b a,b 未知时,给出来了如何更新估计参数的方法。
本节我们基于控制器 u u u,来推导如何求取参考模型。首先概述下之前的结论。
1.1 被控对象
假设存在一个单输入单输出的标量系统,其模型表达式为式 (1)
x ˙ = a x + b u (1) \dot{x} = a x + b u \tag{1} x˙=ax+bu(1)
其中 x x x 表示系统状态, u u u 表示系统控制输入, a , b a,b a,b 是常数。
1.2 参考模型
关于参考模型,我们有
x ˙ r = a r x r + b r r (2) \dot{x}_r = a_r x_r + b_r r \tag{2} x˙r=arxr+brr(2)
其中 a r < 0 a_r<0 ar<0。因为只有 a r a_r ar 是负定的,系统才存在平衡状态。
1.3 跟踪控制器
因此,可以设计控制器为
u = a r − a b x + b r b r − K b e (3) \begin{aligned} u &= \frac{a_r-a}{b}x + \frac{b_r}{b} r - \frac{K}{b} e \end{aligned} \tag{3} u=bar−ax+bbrr−bKe(3)
2 参考模型的选择
在式 (3) 这种形式下的控制器是可以让被控系统实现对参考模型的跟随的。观察式 (3),我们知道 u u u 是由变量 x , r , e x,r,e x,r,e 和参数 a , b , a r , b r a,b, a_r, b_r a,b,ar,br 共同决定的。在之前的文章分析中,我们假定 a r , b r a_r, b_r ar,br 是已知的,分析了 a , b a,b a,b。本文接下来将假定 a , b a,b a,b 已知,分析如何求取想要的参考模型,也就是 a r , b r a_r, b_r ar,br 的值。
式 (3) 形式比较复杂,并且 a r , b r a_r, b_r ar,br 的影响关系不够清晰。我们这里引入两个参数 k 1 , k 2 \red{k_1}, \red{k_2} k1,k2 来简化下,令 u = k 1 x + k 2 r − K b e u = \red{k_1} x + \red{k_2} r - \frac{K}{b} e u=k1x+k2r−bKe,有
u = a r − a b x + b r b r − K b e = k 1 x + k 2 r − K b e (4) \begin{aligned} u &= \frac{a_r-a}{b}x &+ \frac{b_r}{b} r &- \frac{K}{b} e \\ &= \red{k_1} x &+ \red{k_2} r &- \frac{K}{b} e \end{aligned} \tag{4} u=bar−ax=k1x+bbrr+k2r−bKe−bKe(4)
于是我们可以得到一个更简便的描述方式
k 1 = a r − a b ⇒ a r − a = b k 1 k 2 = b r b ⇒ b r = b k 2 (5) \begin{aligned} \red{k_1} &= \frac{a_r-a}{b} &\Rightarrow ~ a_r - a &= b \red{k_1} \\ \red{k_2} &= \frac{b_r}{b} &\Rightarrow ~~~~~~~~b_r &= b \red{k_2} \end{aligned} \tag{5} k1k2=bar−a=bbr⇒ ar−a⇒ br=bk1=bk2(5)
得到的式 (5) 将 a r , b r a_r, b_r ar,br 独立开来了。我们能够很清晰的看到, a r a_r ar 由 a , b , k 1 a,b,\red{k_1} a,b,k1 决定, b r b_r br 由 b , k 2 b,\red{k_2} b,k2 决定,并且二者从形式上互不影响。
接下来,只需要调整 k 1 , k 2 \red{k_1}, \red{k_2} k1,k2 使参考模型达到想要的效果即可。同时被控对象也是一定能同步跟随的。
3 实验验证
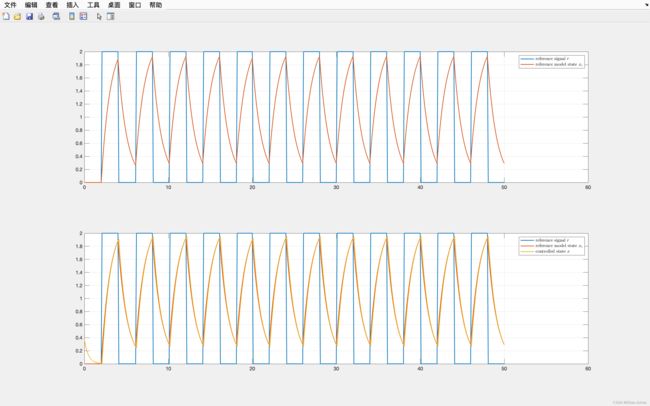
3.1 k 1 = − 5 , k 2 = 2 \red{k_1} = -5, \red{k_2} = 2 k1=−5,k2=2
令 k 1 = − 5 , k 2 = 2 \red{k_1} = -5, \red{k_2} = 2 k1=−5,k2=2,看下程序运行效果,虽然参考模型效果不太好,但是被控系统依然能跟随着参考模型。
3.2 k 1 = 5 , k 2 = − 2 \red{k_1} = 5, \red{k_2} = -2 k1=5,k2=−2
令 k 1 = 5 , k 2 = − 2 \red{k_1} = 5, \red{k_2} = -2 k1=5,k2=−2,可以看到参考模型本身已经崩溃了,那就证明参数不合适,再调整。
3.3 k 1 = − 5 , k 2 = − 2 \red{k_1} = -5, \red{k_2} = -2 k1=−5,k2=−2
令 k 1 = − 5 , k 2 = − 2 \red{k_1} = -5, \red{k_2} = -2 k1=−5,k2=−2,对比实验 3.1,感觉参考模型状态 x r x_r xr 和参考信号 r r r 位于纵轴的两侧。这里分享一点调整经验,之所以会位于两侧是因为参数 b r b_r br 取反了造成的,这时将 k 2 \red{k_2} k2 取相反数即可,对应的 b r b_r br 也就回来了。
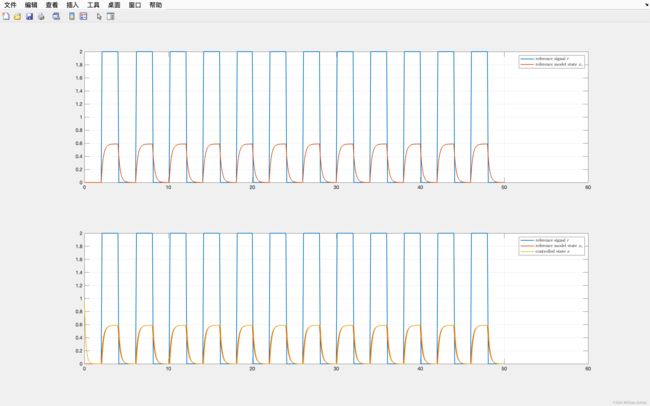
3.4 k 1 = − 10 , k 2 = 2 \red{k_1} = -10, \red{k_2} = 2 k1=−10,k2=2
3.5 实验用程序
clear
clc
%% Initial states
% controlled system
a = 1.6;
b = 0.5;
x(1,1) = rand;
u(1,1) = rand;
% reference model
% a_r = -4;
% b_r = 4;
k_1 = -10;
k_2 = 2;
a_r = a + b*k_1;
b_r = b*k_2;
x(1,1) = rand;
x_r(1,1) = 0;
r(1,1) = 0;
% adaptive parameters
K = 1;
%% Time parameters
tBegin = 0;
tFinal = 50;
dT = 0.1;
times = (tFinal-tBegin)/dT;
t(1,1) = tBegin;
% Iteration
for k=1:times
% record time
t(:,k+1) = t(:,k) + dT;
% update x_r
if mod(t(:,k),4) >= 2
% non-control
r(:,k+1) = 2;
else
r(:,k+1) = 0;
end
dot_x_r = a_r * x_r(:,k) + b_r * r(:,k+1);
x_r(:,k+1) = x_r(:,k) + dT * dot_x_r;
% calculate error
e = x(:,k) - x_r(:,k);
% calculate input
u(:,k+1) = (a_r-a)/b * x(:,k) + b_r/b * r(:,k) - K/b * e;
% update controlled system
dot_x = a * x(:,k) + b * u(:,k+1);
x(:,k+1) = x(:,k) + dT * dot_x;
end
%%
subplot(2,1,1)
plot(t,r, t,x_r, 'linewidth',1.5)
legend('reference signal $r$', 'reference model state $x_r$', 'interpreter','latex')
grid on
subplot(2,1,2)
plot(t,r, t,x_r, t,x, 'linewidth',1.5)
legend('reference signal $r$', 'reference model state $x_r$', 'controlled state $x$', 'interpreter','latex')
grid on
4 结论
总之,得到参考模型参数 a r , b r a_r, b_r ar,br 与被控对象 a , b a,b a,b 之间的关系后,不停的调节参数 k 1 , k 2 \red{k_1}, \red{k_2} k1,k2 即可。调整出来的参考模型不仅符合自己的预期(当然,什么是预期效果只有自己知道),同时还满足跟踪条件。