机器学习——sigmoid、tanh、relu等激活函数总结
一、什么是激活函数?
一个神经元会同时接收多个信号,然后将这些信号乘以一定权重求和,再用函数处理后再输出新的信号。对神经元的输入进行处理,以获得输出的函数称为激活函数。
二、为什么要用激活函数?
- 激活函数对模型学习、理解非常复杂和非线性的函数具有重要作用。
- 激活函数可以引入非线性因素。如果不使用激活函数,则输出信号仅是一个简单的线性函数。线性函数一个一级多项式,线性方程的复杂度有限,从数据中学习复杂函数映射的能力很小。没有激活函数,神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。
- 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。
三、为什么激活函数需要非线性函数?
- 假若网络中全部是线性部件,那么线性的组合还是线性,与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
- 使用非线性激活函数 ,以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数,能够从输入输出之间生成非线性映射。
四、常见的激活函数
1. sigmoid函数
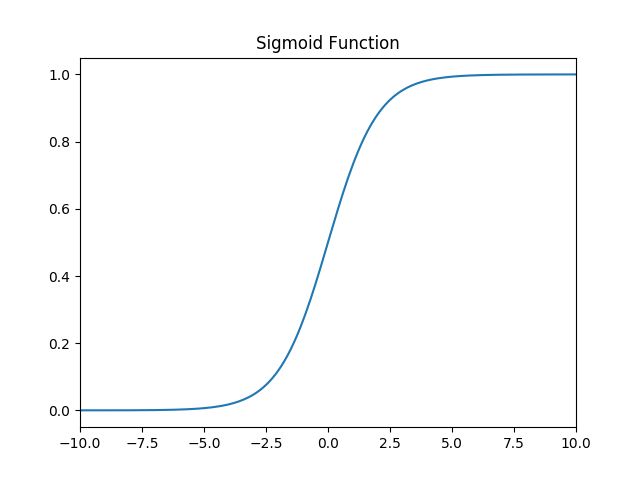
sigmoid函数是最常用的连续、平滑的激励函数,也被称作逻辑函数(Logistic函数)。用于隐层神经元输出,可以将一个实数映射到(0,1)的区间,用来做二分类。
a. 函数定义: f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1,值域: ( 0 , 1 ) (0,1) (0,1)。
c. 导数:: f ′ ( x ) = 1 1 + e − x ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) f^{'}(x)=\frac{1}{1+e^{-x}}\left( 1- \frac{1}{1+e^{-x}} \right)=f(x)(1-f(x)) f′(x)=1+e−x1(1−1+e−x1)=f(x)(1−f(x))
d. 特点:当 x = 10 x=10 x=10,或 x = − 10 x=-10 x=−10, f ′ ( x ) ≈ 0 f^{'}(x) \approx0 f′(x)≈0,当 x = 0 x=0 x=0 f ′ ( x ) = 0.25 f^{'}(x) =0.25 f′(x)=0.25。
2. Tanh函数
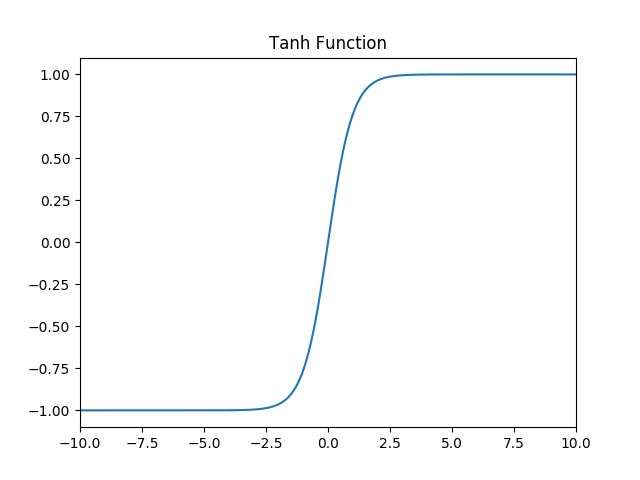
a. 函数定义: f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x,值域: ( − 1 , 1 ) (-1,1) (−1,1) 。
c. 导数: f ′ ( x ) = − ( t a n h ( x ) ) 2 f^{'}(x)=-(tanh(x))^2 f′(x)=−(tanh(x))2
d. 特点:当 x = 10 x=10 x=10,或 x = − 10 x=-10 x=−10, f ′ ( x ) ≈ 0 f^{'}(x) \approx0 f′(x)≈0,当 x = 0 x=0 x=0 f ‘ ( x ) = 1 f^{`}(x) =1 f‘(x)=1。
3. ReLU函数
ReLU是神经网络最常用的非线性函数。其函数为max(0,x),连续但不平滑。
a. 函数定义: f ( x ) = m a x ( 0 , x ) f(x) = max(0, x) f(x)=max(0,x)值域: [ 0 , + ∞ ) [0,+∞) [0,+∞)。
c. 导数: f ′ ( x ) = { 0 , x < 0 1 , x > 0 u n d e f i n e d , x = 0 f^{'}(x)=\begin{cases} 0,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases} f′(x)=⎩⎪⎨⎪⎧0,x<01,x>0undefined,x=0
d. 特点:具有单侧抑制;相对宽阔的兴奋边界;稀疏激活性等性质。
4. Leak Relu 激活函数
a. 函数定义: f ( x ) = { a x , x < 0 x , x > 0 f(x) = \left\{ \begin{aligned} ax, \quad x<0 \\ x, \quad x>0 \end{aligned} \right. f(x)={ax,x<0x,x>0,值域: ( − ∞ , + ∞ ) (-∞,+∞) (−∞,+∞)
c. 导数: f ′ ( x ) = { a , x < 0 1 , x > 0 u n d e f i n e d , x = 0 f^{'}(x)=\begin{cases} a,x<0 \\ 1,x>0 \\ undefined,x=0\end{cases} f′(x)=⎩⎪⎨⎪⎧a,x<01,x>0undefined,x=0
5. ELU函数
a. 函数定义: f ( x ) = { a ( e x − 1 ) , x < 0 x , x > 0 f(x) = \left\{ \begin{aligned} a(e^x-1), \quad x<0 \\ x, \quad x>0 \end{aligned} \right. f(x)={a(ex−1),x<0x,x>0,值域: ( − a , + ∞ ) (-a,+∞) (−a,+∞)。
6. SoftPlus 函数
a. 函数定义: f ( x ) = l n ( 1 + e x ) f(x) = ln( 1 + e^x) f(x)=ln(1+ex)值域: $ (0,+∞) $
c. 导数: f ′ ( x ) = e x 1 + e x f^{'}(x)=\frac{e^x}{1 + e^x} f′(x)=1+exex
7. softmax函数
softmax 函数可以把它的输入,通常被称为 logits 或者 logit scores,处理成 0 到 1 之间,并且能够把输出归一化到和为 1。这意味着 softmax 函数与分类的概率分布等价。它是一个网络预测多酚类问题的最佳输出激活函数。
a. 函数定义: P ( i ) = e x p ( θ i T x ) ∑ k = 1 K e x p ( θ i T x ) P(i) = \frac{exp(\theta_i^T x)}{\sum_{k=1}^{K} exp(\theta_i^T x)} P(i)=∑k=1Kexp(θiTx)exp(θiTx),其中, θ i \theta_i θi 和 x x x 是列向量, θ i T x \theta_i^T x θiTx 可能被换成函数关于 x x x 的函数 f i ( x ) f_i(x) fi(x)。
五、如何选择激活函数
选择一个适合的激活函数并不容易,需要考虑很多因素,通常的做法是,如果不确定哪一个激活函数效果更好,可以把它们都试试,然后在验证集或者测试集上进行评价。然后看哪一种表现的更好,就去使用它。以下是常见的选择情况:
- 如果输出是 0、1 值(二分类问题),则输出层选择 sigmoid 函数,然后其它的所有单元都选择 Relu 函数。
- 如果在隐藏层上不确定使用哪个激活函数,那么通常会使用 Relu 激活函数。有时,也会使用 tanh 激活函数,但 Relu 的一个优点是:当是负值的时候,导数等于 0。
- sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
- tanh 激活函数:tanh 是非常优秀的,几乎适合所有场合。
- ReLu 激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用 ReLu 或者 Leaky ReLu,再去尝试其他的激活函数。
- 如果遇到了一些死的神经元,我们可以使用 Leaky ReLU 函数。