笔记一|Selective Search for Object Recognition

1. 相关论文

分割方面【Felzenszwalb,P.F.,&Huttenlocher,D.P.(2004)】Efficent graph-based image segmentation

---

论文思路：用分割的方法产生一系列小的class independent object locations

论文链接：Selective Search

论文将分为以下几个部分记录

A selective search方法的介绍（已完成）

• 产生目标定位框（object locations boxes）的算法介绍
• 算法的决策方法
• 最终用于目标识别的区域

B 与目标识别的结合

C 算法的评估

---

一 selective search

1 聚合算法：将图像分成区域（regions），并提取相应的边界框（boxes）

1.1 阅读中的自问自答

【region是什么】从图像中提取区域，就是将图像中相似的像素集聚一起，形成一个又一个region。

在算法中实现为将图像看成是由许许多多不相交且并集为整个图像的区域所组成的

【算法的大白话叙述】从初始划分的region出发，逐步计算各region之间的相似度，两个相似的region合并成一个新的region，直至只剩下一个region，就是整张图，此时停止。

【为什么要对图像不断聚合】在这个过程中，我们可以从不断生成的区域上提取对应的边界框，这些盒子随着region的变换，包含了不同位置的像元，也形成了不同的大小这些盒子就是我们目标识别所需要的数据单位

【生成初始的regions是怎么实现的】生成的算法请看Felzenszwalb和Huttenlocher的分割算法

1.2 算法（Hierachical Group Algorithm）的介绍

A 层级的理解

B 用到的数据集合

• 相似集：存储区域之间的相似度的值
• regions集：集合存储了算法过程中生成的各个区域，不同层级的都有

C 算法流程的叙述 

a 初始化

定义相似集，初始为空

初始化,区域是从上述提到的分割得到的

b 聚合，循环进行

•         对于相邻的region pair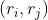，计算其相似度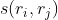

                       更新

•         然后循环遍历:
  1.         找到最高相似度的区域对
  2.         将该区块对中的两个区域合并
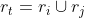
  3.         移除集合所有包含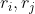的区域对相似度
  4.         计算合并后产生的新的区域与其相邻区域的相似度，记录在中
  5.         更新S，R集合：

 直到所有的区块融合成一整个区块。

c 算法输出

从R中所有的区域里提取对应的目标定位盒子L

1.3 区域融合的判断方法：相似度

本小节介绍了设计相似度的度量方法，用于在1.2算法中判断哪些区域需要融合成一个新的区域

在设计时应当考虑的是：

•  互补：各方法衡量的维度应该是不同的，不要重叠
•  度量方法可以快速计算：文中强调的hierarchy（层次结构）的特性就体现了，由上述算法可知，在遍历的时候，区块不断融合再重新计算相似度，如果每次遍历都要重新计算所有的像素点，那么计算量就是巨大的，文中提出的方法在计算像素度时可以层级传递，就方便了对于新产生的区块计算相似度

1.3.1度量方法的介绍（complementary Similarity Measures）

     文中设计了四种相似度指标，相似度的数值范围是[0,1]

A 色彩相似度

【解读】计算了重叠的颜色频率和

【公式各符号含义】

n（bins的总数量）：每个颜色通道设定25个bins（直方图相关的知识），那么对于三通道的颜色直方图，一共有75个bins（简单理解即直方图的横坐标有75个）

：第i个region有颜色直方图，其第k个bin上的值

颜色直方图会用L1范数归一化（的L1范数为各元素的绝对值的和）

【设计的层次架构带来的好处】

颜色直方图是可以通过层次架构传播的：

size就是区块中的像素数目，这样做便于高层次区域相似度的计算

B 纹理相似度

也是计算了重叠度，与颜色相似度可以用相同的公式传播

【符号含义】

t的向量是由另一篇文章中提到的方法得到的，目前还没有学习，故先不叙述

C 尺寸相似度

分母是整张图的大小

【设计出发点】这个相似度会使小的区块率先融合，且会使待融合的区块都在相似的尺寸，这样就能够实现在整张图像的各个位置都生成各种尺寸的区块（防止从一个小区块出发逐渐融合相邻区块至结束，然后之只能在起始位置找到小尺寸的区块，其他位置都是其融合的结果）

D 与边界框的相似度

【设计思路】

这个相似度可以让两个区域避免以奇怪的形状融合在一起

令是紧紧环绕的盒子，则上式的第二项的分子部分计算的就是两个区域在盒子中没有占据的部分

1.3.2 本文的相似度度量方法

根据上式四个相似度，本文中设计的相似度度量方法为上述四种相似度的线性组合

1.3.3 多样化决策的其他设计思路

        多样化决策还可以是改变初始化的区块，但是文中提到，前述中Felzenswalb和Huttenlocher设计的分割算法产生的region的计算速度是最快的，所以没有考虑改变分割的策略，但是可以改变算法中的阈值参数（变相改变了分割的结果），还可以改变色彩空间（RGB,I,Lab等）

1.4 生成combined object hypothese set

学习了度量方法，再返回到层级算法来看：

        第二部分的四类相似度的线性组合决定了算法是怎么将区域聚合的，因此对线性组合的四个权值取不同值，就是不同的决策，也就产生了不同的locations

        我们可以将不同决策下的locations结合生成combined object hypotheses set，然后对其进行排序，因为若考虑多决策下的locations数量可能很庞大

        排序的方法，先在每个决策产生的regions的集合内部，对每个region进行赋值

给定一个决策strategy j

令为在整个层级结构中处于位置i的区域（i=1代表最高层，也就是覆盖了整个图像的区域，可以理解为第几次融合生成的区域，越是时间在后面融合的区域其i值越小）

给一个赋值

这样就可以对最终的集合进行排序了

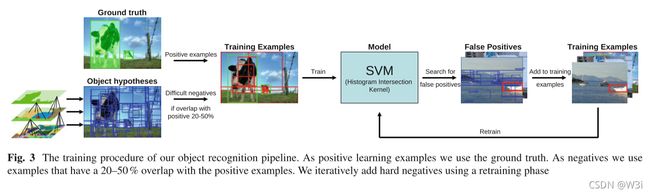
2 selective search with 目标识别

挖坑  

 从最左侧是图片也能看到算法运作的流程，下一层的小区域被抓取融合成上一层的新区域

colour-SIFT descriptors ( van de Sande et al.2020

分类器

Shogun Toolbox源码

3 评估算法的优越性

3.1 Flat Versus Hierachy

实验组一：分割算法（Felzenszwalb和Huttenlocher）得到的不同参数k下的区域

hierachical算法得到的region

结果：本文算法的MABO更高

3.2 diversifications strategies

多策略得到的MABO更高