（Water Filling）注水算法原理与实现

问题背景与建模

考虑一个多用户多输入单输出MU-MISO下行通信场景，基站端配置有$N$根天线，其服务该小区下$K$个单天线用户。假定信道为平坦瑞利衰落信道，记为$\mathbf{H}\in {\mathcal{C}}^{N\times K}$，基站最大发射功率为$P$。假设波束赋形采用Zero Forcing,若记
$$\mathbf{W}=\mathbf{H}({\mathbf{H}}^H\mathbf{H}{)}^{-1}$$

注意$\mathbf{W}$并不是最终的波束赋形矩阵，因为还没有考虑功率约束以及进一步的功率分配。

则第$k$个用户的波束方向为
$${\tilde{\mathbf{w}}}_k=\frac{{\mathbf{w}}_1}{||{\mathbf{w}}_1|{|}_2}$$

记$\tilde{\mathbf{W}}=[{\tilde{\mathbf{w}}}_1,...,{\tilde{\mathbf{w}}}_K]$，功率分配矩阵为

$$\mathbf{P}=\text{diag}(P_1,...,P_K)$$

则最终的波束赋形矩阵为
$${\mathbf{W}}_{\text{ZF}}=\tilde{\mathbf{W}}\cdot \sqrt{\mathbf{P}}$$

若不考虑功率分配，显然$\forall k,P_k=P/K$。

若记基站发送的符号向量为$\mathbf{s}=[s_1,...,s_K]$，且满足$\mathbb{E}[\mathbf{s}{\mathbf{s}}^H]={\mathbf{I}}_K$，则用户$k$接收到的信号为
$$y_k={\mathbf{h}}_k^H{\mathbf{w}}_k{s}_k+n_k$$

这是因为ZF完全消除了用户间干扰！此时SINR就是SNR。

而对于其他的波束赋形，如MMSE、MRT等，由于用户间干扰不能完全去除，用户$k$的SINR里面还嵌入有其他用户的功率，本文water-filling求出的解只是对于ZF波束赋形是最优的，对于其他的beamforming, 只能说是次优和heuristic的。

其中$n_k$为用户$k$处的噪声，$n_k\sim \mathcal{C}\mathcal{N}(0,1)$。第$k$个用户的信噪比SNR为
$${\gamma }_k=||{\mathbf{h}}_k^H{\mathbf{w}}_k|{|}_2^2=P_k||{\mathbf{h}}_k^H{\tilde{\mathbf{w}}}_k|{|}_2^2$$

第$k$个用户的信息速率为
$$R_k=\log (1+{\gamma }_k)$$

实际上这是肯定不可能达到的，只具有理论分析上的意义。

现在希望合理的分配功率来使得加权和速率最大，即
$$\begin{gathered} \underset{P_1,...,P_K}{\max }\sum _{k=1}^K{\alpha }_k{R}_k \\ \text{s.t.}\sum _{k=1}^K{P}_k=P \\ {P}_k\ge 0 \end{gathered}$$

上面直接让各用户功率之和等于最大发射功率，即让本来的不等式约束变为严格等于。这是因为最优解必然是满足这一点的。

问题求解

$$\begin{array}{rl}& \sum _{k=1}^K{\alpha }_k{R}_k\\ & =\sum _{k=1}^K{\alpha }_k\log (1+P_k||{\mathbf{h}}_k^H{\tilde{\mathbf{w}}}_k|{|}_2^2)\\ & =\sum _{k=1}^K{\alpha }_k\log (\frac{1}{||{\mathbf{h}}_k^H{\tilde{\mathbf{w}}}_k|{|}_2^2}+P_k)+\sum _{k=1}^K{\alpha }_k\log ||{\mathbf{h}}_k^H{\tilde{\mathbf{w}}}_k|{|}_2^2\end{array}$$

定义
$$L_k=\frac{1}{||{\mathbf{h}}_k^H{\tilde{\mathbf{w}}}_k|{|}_2^2}$$

则优化问题变为
$$\begin{gathered} \underset{P_1,...,P_K}{\max }\sum _{k=1}^K{\alpha }_k\log (L_k+P_k) \\ \text{s.t.}\sum _{k=1}^K{P}_k=P \\ {P}_k\ge 0 \end{gathered}$$

可以看到与大多地方介绍注水算法有些许不同，此处其实是更一般的情况，即不同用户的权重或者priority是不同的。
该问题是凸优化问题，且Slater条件满足，此时KKT条件是最优性的充要条件。
拉格朗日函数为
$$L=-\sum _{k=1}^K{\alpha }_k\log (L_k+P_k)-\sum _{k=1}^K{\lambda }_k{P}_k+\mu \left(\sum _{k=1}^K{P}_k-P\right)$$

互补松弛条件为
$${\lambda }_k{P}_k=0$$

平稳性条件为
$$-\frac{{\alpha }_k}{L_k+P_k}-{\lambda }_k+\mu =0$$

所以有
$$\left(\mu -\frac{{\alpha }_k}{L_k+P_k}\right)P_k=0$$

当$\mu \ge \frac{{\alpha }_k}{L_k}$时，必然有$P_k=0$;

当$\mu <\frac{{\alpha }_k}{L_k}$时，有
$$P_k=\frac{{\alpha }_k}{\mu }-L_k$$

换句话说，

当$\frac{L_k}{{\alpha }_k}\ge \frac{1}{\mu }$时，$\frac{P_k}{{\alpha }_k}=0$

当$\frac{L_k}{{\alpha }_k}<\frac{1}{\mu }$时，$\frac{P_k}{{\alpha }_k}=\frac{1}{\mu }-\frac{L_k}{{\alpha }_k}$

算法描述

上面的结果可以描述为一个往容器中注水的过程。考虑如下这样一个“水槽”（2维）

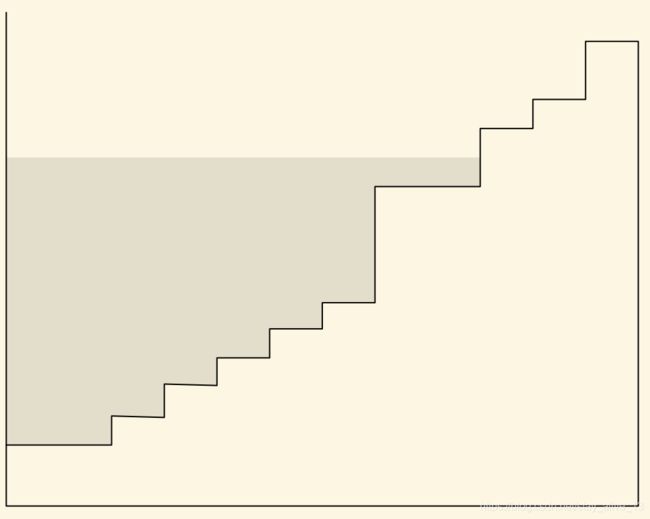
第$k$个台阶的宽即为${\alpha }_k$，高（离槽底）为$L_k/{\alpha }_k$，对应的面积为$L_k$，那么功率分配的过程就是将功率P像是注水一样进行分配，倒入这个水槽。若台阶太高（信道太差），则该台阶上不会分配到水。对于非加权的简单情况，每一个台阶的宽都相等，为单位长度。显然注水之后的水位线即为
$$\frac{1}{\mu }$$

上面的图其实是按照不同用户的$L_k/{\alpha }_k$进行了排序。实际实现时，可视采用的算法决定是否进行排序。

算法实现

可以看出，如果我们能知道最终的水位线$1/\mu$，那么问题就十分简单，只需要根据每个用户的台阶高度决定是否给该用户分配功率以及分配多少。但是这个水位线并非提前就知道的。所以实际实现时有两个方法

• 先明确水位线，然后分配
• 不具体求水位线，而是将用户按$L_k/{\alpha }_k$进行排序，然后确定哪些用户需要注水

方法一

其算法流程为：

$\mathcal{K}=\{1,...,K\}$

$1/\hat{\mu }=(P+{\sum }_{k\in \mathcal{K}}{L}_k)/{\sum }_{k\in \mathcal{K}}{\alpha }_k$（假设每个用户都分配）

$\hat{k}=\arg {\max }_{k\in \mathcal{K}}{L}_k/{\alpha }_k$

$\text{while}{L}_{\hat{k}}/{\alpha }_{\hat{k}}\ge 1/\hat{\mu }$

$\mathcal{K}=\mathcal{K}-\hat{k}$

$1/\hat{\mu }=(P+{\sum }_{k\in \mathcal{K}}{L}_k)/{\sum }_{k\in \mathcal{K}}{\alpha }_k$

$\hat{k}=\arg {\max }_{k\in \mathcal{K}}{L}_k/{\alpha }_k$

于此便可求出最终的水位线$1/\mu$，有了水位线那么分配就很简单了。基于上述方法的MATLAB实现代码如下：

function palloc_matrix = water_filling1(loss, P, A)
% loss, Kx1向量，即L
% P, 要分配的总功率
% A, 对角阵，即权重alpha
% palloc_matrix, 对角阵，功率分配结果，迹等于P

	K = length(loss); % 用户数
    
	w = diag(A); % width, 台阶宽度
	h = loss./w; % height, 台阶高度
	
    allo_set = 1:K; % 初始化要注水用户的索引集合
    level = (P+sum(loss(allo_set>0)))/sum(w(allo_set>0)); % “虚拟”水位线
    [h_hat, k_hat] = max(h(allo_set>0));
    
    while h_hat>=level
        
        allo_set(k_hat) = -1;
        level = (P+sum(loss(allo_set>0)))/sum(w(allo_set>0)); % “虚拟”水位线
        [h_hat, k_hat] = max(h(allo_set>0));
    
    end
    
    palloc_matrix = zeros(K);
    for k = 1:K
        if allo_set(k)>0
            palloc_matrix(k, k) = (level - h(k))*w(k);
        end
    end
    
end

方法二

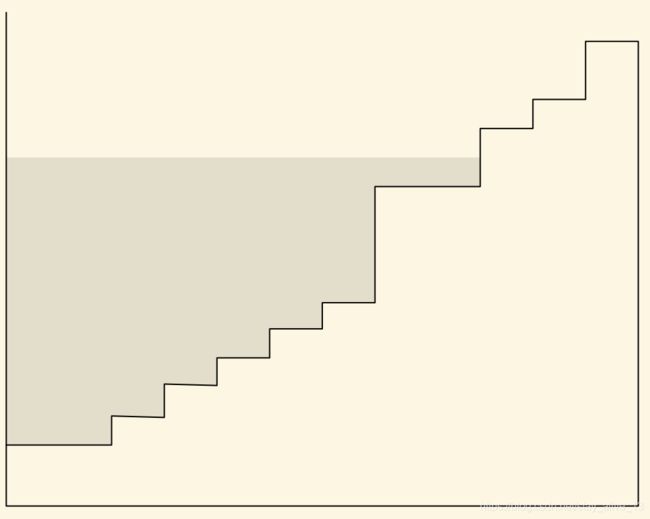
根据$L_k/{\alpha }_k$进行升序排序，可以确定最后一个需要注水的索引，然后对其及其之前的用户进行注水。首先给出排序后第$n$个台阶要注水的判断依据：
$$\sum _{j=1}^{n-1}{\alpha }_j\times \frac{L_n}{{\alpha }_n}-\sum _{j=1}^{n-1}{L}_j>P$$

注意上式中的下标是排序后的，代码实现时需注意。

有了这个判断依据之后，便可以通过线性搜索或是二分搜索来确定最后一个要注水的台阶。

线性搜索

function palloc_matrix = water_filling2(loss, P, A)
	
	K = length(loss);
    
	w = diag(A); % 台阶宽度
	h = loss./w; % 台阶高度
	
	[h_sorted, h_idx] = sort(h); % 根据台阶高度升序排序
	w_sorted = w(h_idx);
    
    % 线性搜索，从后往前确定最后一个需要注水的台阶
    for i = K:-1:1
        
        w_tmp = sum(w_sorted(1:i-1)); % 当前台阶前面所有台阶的宽度之和
        h_tmp = h_sorted(i); % 当前台阶的高度
        
        % 把当前台阶之前的台阶注水到与当前台阶同高还有剩余水
        if w_tmp*h_tmp-sum(h_sorted(1:i-1).*w_sorted(1:i-1))<P
            idx = i;
            break;
        end
        
    end
    
    w_filled = sum(w_sorted(1:idx)); % 需要注水的所有台阶的总宽度
    h_filled = (P+sum(h_sorted(1:idx).*w_sorted(1:idx)))/w_filled; % 最终的水位线
	
	p_allocate = zeros(1, K);
    p_allocate(1:idx) = w_sorted(1:idx).*(h_filled-h_sorted(1:idx));
	
    % 恢复原来顺序
    [~, back_idx] = sort(h_idx);
    p_allocate = p_allocate(back_idx);
    
    palloc_matrix = diag(p_allocate);
    
end

二分搜索

function palloc_matrix = water_filling3(loss, P, A)
	
	K = length(loss);
    
	w = diag(A);
	h = loss./w;
	
	[h_sorted, h_idx] = sort(h);
	w_sorted = w(h_idx);
    
    % 二分搜索
    
    % 对最后一个台阶单独讨论
    if sum(w_sorted(1:K-1))*h_sorted(K)-sum(h_sorted(1:K-1).*w_sorted(1:K-1))<P
        idx = K;
    else
        idx_max = K;
        idx_min = 1;

        idx = -1;

        while 1
            idx_mid = floor(.5*(idx_max+idx_min));
            w_tmp = sum(w_sorted(1:idx_mid-1));
            h_tmp = h_sorted(idx_mid);
            if w_tmp*h_tmp-sum(h_sorted(1:idx_mid-1).*w_sorted(1:idx_mid-1))<P
                idx_min = idx_mid;
            else
                idx_max = idx_mid;
            end
            if idx_min+1 == idx_max
                idx = idx_min;
                break
            end
        end
    end
    
    w_filled = sum(w_sorted(1:idx));
    h_filled = (P+sum(h_sorted(1:idx).*w_sorted(1:idx)))/w_filled;
	
	p_allocate = zeros(1, K);
    p_allocate(1:idx) = w_sorted(1:idx).*(h_filled-h_sorted(1:idx));
	
    [~, back_idx] = sort(h_idx);
    p_allocate = p_allocate(back_idx);
    
    palloc_matrix = diag(p_allocate);
    
end

测试代码

while 1
    
    K = 4;
    P = 3;
    alpha = abs(rand(K, 1));
    A = diag(alpha);
    loss = abs(randn(K,1));
    
    % 如未安装CVX，将该代码段注释掉
    %=============================================
    cvx_begin quiet

        variable p(K)
        minimize -sum(alpha.*log(loss+p))
        subject to
            0<=p
            sum(p)==P

    cvx_end
    %=============================================

    p
    p1 = diag(water_filling1(loss,P, A))
    p2 = diag(water_filling2(loss,P, A))
    p3 = diag(water_filling3(loss,P, A))
    
end

总结

本文以加权和速率为背景引出了一般化的注水算法的问题背景，之后从KKT条件导出了该问题解的特点，该特点即表现为一个注水过程。对于本文描述的有加权的情况，形象的，每个用户对应的“台阶”宽度是不一样的，台阶越宽，表示其权重越高。最后给出了实现算法即MATLAB代码。

值得注意的是，本文前面提到，该结果是在ZF预编码的前提下推导得到的，也就是说注水算法得到的功率分配结果是ZF预编码下的最优分配方案，但对于其他预编码，如MRT、MMSE，只是次优的。