一文搞懂时序逻辑电路
时序逻辑电路
-
- 1.1 介绍
- 1.2 特点
- 1.3 锁存器
-
- 1.3.1 特点
- 1.3.2 常用锁存器
-
- 1.3.2.1 SR锁存器
-
- 1.3.2.1.1 或非实现
-
- 1.3.2.1.1.1 状态方程
- 1.3.2.1.1.2 状态转换图
- 1.3.2.1.1.3 真值表
- 1.3.2.1.2 与非实现
-
- 1.3.2.1.2.1 状态方程
- 1.3.2.1.2.2 状态转换图
- 1.3.2.1.2.3 真值表
- 1.3.2.2 SR锁存器与非和或非的区别
- 1.3.2.2 门控SR锁存器
-
- 1.3.2.2.1 状态方程
- 1.3.2.2.2 状态转换图
- 1.3.2.2.3 特性表
- 1.3.2.3 门控D锁存器
-
- 1.3.2.3.1 状态方程
- 1.3.2.3.2 状态转换图
- 1.3.2.3.3 真值表
- 1.4 触发器
-
- 1.4.1 分类
-
- 1.4.1.1 逻辑功能划分
-
- 1.4.1.1.1 RS触发器
- 1.4.1.1.2 D触发器
- 1.4.1.1.3 JK触发器
-
- 1.4.1.1.3.1 状态方程
- 1.4.1.1.3.2 状态转换图
- 1.4.1.1.3.3 真值表
- 1.4.1.1.4 T触发器
-
- 1.4.1.1.4.1 状态方程
- 1.4.1.1.4.2 状态转换图
- 1.4.1.1.4.3 真值表
- 1.4.1.2 电路结构和触发方式划分
-
- 1.4.1.2.1 同步触发器
- 1.4.1.2.2 主从触发器
- 1.4.1.2.3 边沿触发器
- 1.4.2 触发器之间的转换方法
- 1.5 触发器和锁存器的区别
- 1.6 常用时序电路
-
- 1.6.1 寄存器
-
- 1.6.1.1 介绍
- 1.6.1.2 分类
-
- 1.6.1.2.1 数据寄存器
- 1.6.1.2.2 移位寄存器
- 1.6.1.2.3 双向移位寄存器/通用寄存器
- 1.6.2 计数器
-
- 1.6.2.1 介绍
- 1.6.2.2 分类
-
- 1.6.2.2.1 计数功能分
- 1.6.2.2.2 进位基数分
- 1.6.2.2.3 进位方式分
- 1.7 时序逻辑电路的一般模型和结构特点
- 1.8 按其状态的改变方式不同分类
-
- 1.8.1 同步时序逻辑电路
-
- 1.8.1.1 三组逻辑表达式
- 1.8.1.2 按其输入和输出的关系不同
-
- 1.8.1.2.1 米里型时序逻辑电路
- 1.8.1.2.2 摩尔型时序逻辑电路
- 1.8.2 异步时序逻辑电路
- 1.9 功能描述方法
-
- 1.9.1 逻辑表达式
- 1.9.2 状态转换表
- 1.9.3 状态转换图
- 1.9.4 时序图
- 1.10 同步时序逻辑电路分析方法
- 1.11 自启动能力
- 1.12 同步时序逻辑设计
-
- 1.12.1 步骤
- 1.12.2 状态化简
-
- 1.12.2.1 判断两个状态是否等效的条件
- 1.12.2.2 隐含表法
-
- 1.12.2.2.1 隐含表化简步骤
- 1.12.3 状态编码
1.1 介绍
输出往往反馈到输入端,与输入变量一起决定电路的输出状态。
1.2 特点
任意时刻输出不仅取决于该时刻输入变量的状态,而且还与原来的状态有关。
1.3 锁存器
1.3.1 特点
- 有两个互补的输出端 Q Q Q和 Q ‾ \overline{Q} Q,当 Q Q Q = 1时, Q ‾ \overline{Q} Q = 0;而当 Q Q Q = 0时, Q ‾ \overline{Q} Q = 1。
- 有两个稳定状态,通常将 Q Q Q = 1和 Q ‾ \overline{Q} Q = 0称为1状态,而当 Q Q Q = 0和 Q ‾ \overline{Q} Q = 1称为0状态,若输入不发生变化,锁存器必定处于其中一个状态,并且长期保持下去。
- 在输入信号的作用下,锁存器可以从一个稳定状态转换到另一个稳定状态。
- 我们把输入信号发生变化之前的锁存器状态称为现态(PS),用 Q n Q^n Qn和 Q ‾ n \overline{Q}^n Qn来表示,而把输入信号发生变化后锁存器所进入的状态称为次态(NS),用 Q n + 1 Q^{n+1} Qn+1和 Q ‾ n + 1 \overline{Q}^{n+1} Qn+1来表示。
1.3.2 常用锁存器
1.3.2.1 SR锁存器
1.3.2.1.1 或非实现
1.3.2.1.1.1 状态方程
{ Q n + 1 = S + R ‾ Q n S ∙ R = 0 \begin{cases} Q^{n+1} = S + \overline{R}Q^n \\ S \bullet R = 0 \end{cases} {Qn+1=S+RQnS∙R=0
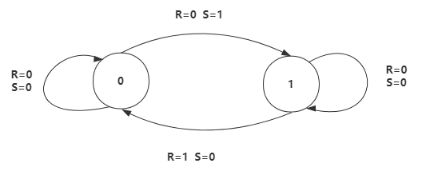
1.3.2.1.1.2 状态转换图
1.3.2.1.1.3 真值表
| R | S | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|
| 0 | 0 | 0 | 保持 Q n Q^n Qn不变 |
| 0 | 0 | 1 | 保持 Q n Q^n Qn不变 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 不稳 |
| 1 | 1 | 1 | 不稳 |
1.3.2.1.2 与非实现
1.3.2.1.2.1 状态方程
{ Q n + 1 = S ‾ ‾ + R ‾ Q n S ‾ + R ‾ = 1 \begin{cases} Q^{n+1} = \overline{\overline{S}} + \overline{R}Q^n \\ \overline{S} + \overline{R} = 1 \end{cases} {Qn+1=S+RQnS+R=1
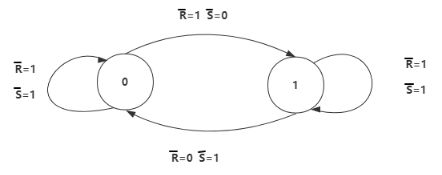
1.3.2.1.2.2 状态转换图
1.3.2.1.2.3 真值表
| R ‾ \overline{R} R | S ‾ \overline{S} S | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|
| 0 | 0 | 0 | 不稳 |
| 0 | 0 | 1 | 不稳 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 保持 Q n Q^n Qn不变 |
| 1 | 1 | 1 | 保持 Q n Q^n Qn不变 |
1.3.2.2 SR锁存器与非和或非的区别
- 与非门是输入低电平控制的器件,即有一个输入为0时,输出就一定是1。
- 或非门是输入高电平控制的器件,输入都是0时,输出才是1。
- 根据真值表可以得到与非门和或非门的置0和置1正好相反。
1.3.2.2 门控SR锁存器
1.3.2.2.1 状态方程
{ Q n + 1 = S + R ‾ Q n S ∙ R = 0 \begin{cases} Q^{n+1} = S + \overline{R}Q^n \\ S \bullet R = 0 \end{cases} {Qn+1=S+RQnS∙R=0
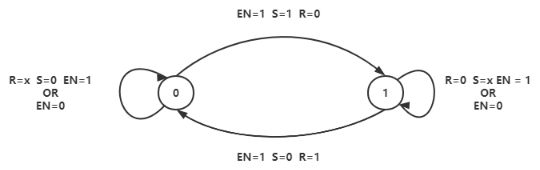
1.3.2.2.2 状态转换图
1.3.2.2.3 特性表
| EN | S | R | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|---|
| 0 | x | x | x | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 0 | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 1 | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 不稳 |
| 1 | 1 | 1 | 1 | 不稳 |
1.3.2.3 门控D锁存器
1.3.2.3.1 状态方程
Q n + 1 = D Q^{n+1} = D Qn+1=D
1.3.2.3.2 状态转换图
1.3.2.3.3 真值表
| EN | D | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|
| 0 | x | x | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
1.4 触发器
1.4.1 分类
1.4.1.1 逻辑功能划分
1.4.1.1.1 RS触发器
和门控RS锁存器情况基本相同
1.4.1.1.2 D触发器
和门控D锁存器情况基本相同
1.4.1.1.3 JK触发器
1.4.1.1.3.1 状态方程
Q n + 1 = J Q n ‾ + K ‾ Q n Q^{n+1} = J\overline{Q^n} + \overline{K}Q^n Qn+1=JQn+KQn
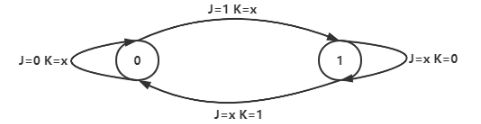
1.4.1.1.3.2 状态转换图
1.4.1.1.3.3 真值表
| EN | J | K | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|---|
| 0 | x | x | x | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 0 | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 1 | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 翻转 |
| 1 | 1 | 1 | 1 | 翻转 |
1.4.1.1.4 T触发器
1.4.1.1.4.1 状态方程
Q n + 1 = Q n ‾ Q^{n+1} = \overline{Q^n} Qn+1=Qn
1.4.1.1.4.2 状态转换图
1.4.1.1.4.3 真值表
| CP | T | Q n Q^n Qn | Q n + 1 Q^{n+1} Qn+1 |
|---|---|---|---|
| 0 | x | x | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 0 | 保持 Q n Q^n Qn不变 |
| 1 | 0 | 1 | 保持 Q n Q^n Qn不变 |
| 1 | 1 | 0 | 翻转 |
| 1 | 1 | 1 | 翻转 |
1.4.1.2 电路结构和触发方式划分
1.4.1.2.1 同步触发器
1.4.1.2.2 主从触发器
- 克服同步触发器的空翻现象。
- 提高触发器工作的可靠性。
- 使触发器在每个时钟脉冲周期内状态只改变一次。
1.4.1.2.3 边沿触发器
触发器仅在时钟脉冲的上下沿到来时才接收输入信号,在脉冲为0或1的时候不接受输入信号。边沿触发器不仅克服了空翻现象,而且大大提高了抗干扰能力。
1.4.2 触发器之间的转换方法
先比较已有触发器和待求触发器的特性方程,求出转换电路的逻辑函数表达式,再根据转换逻辑画出逻辑电路图。
1.5 触发器和锁存器的区别
- 锁存器同其所有的输入信号相关,当输入信号变化时锁存器就变化,没有时钟端。
- 锁存器由电平触发,非同步控制。在使能信号有效时锁存器相当于通路,在使能信号无效时锁存器保持输出状态。
- 锁存器对输入电平敏感,受布线延迟影响较大,很难保证输出没有冒险产生。
- 触发器受时钟控制,只有在时钟触发时才采样当前的输入,产生输出。
- 触发器由时钟沿触发,同步控制。
- 触发器则不易产生冒险。
- 触发器相比较于锁存器优点在于触发器是一个同步双稳态器件,所谓同步,是指触发器的记忆状态按时钟脉冲的边沿来改变。触发器在时钟脉冲的上边沿和下边沿来启动记忆1为数据的方法,提高了逻辑电路的可靠性和工作速度。
1.6 常用时序电路
1.6.1 寄存器
1.6.1.1 介绍
由锁存器或触发器组成,一次能够并行存储n位比特数据的逻辑部件称为寄存器
1.6.1.2 分类
1.6.1.2.1 数据寄存器
并行输入并行输出
1.6.1.2.2 移位寄存器
- 右移寄存器
- 循环右移寄存器
- 左串输入右串输出
- 串行输入并行输出
- 并行输入串行输出
- 左移寄存器
- 循环左移寄存器
- 右端串行输入从左端串行输出
1.6.1.2.3 双向移位寄存器/通用寄存器
- 串入串出
- 串入并出
- 并入串出
- 并入并出
1.6.2 计数器
1.6.2.1 介绍
计数器的功能是记忆脉冲的个数,计数器所能记忆脉冲的最大数目称为该计数器的模,用字母M来表示,构成计数器的核心元件是触发器
1.6.2.2 分类
1.6.2.2.1 计数功能分
- 加法计数器
- 减法计数器
- 可逆计数器
1.6.2.2.2 进位基数分
- 二进制计数器
- 十进制计数器
- 任意进制计数器
1.6.2.2.3 进位方式分
- 同步计数器(并行计数器)
- 异步计数器(串行计数器)
1.7 时序逻辑电路的一般模型和结构特点
时序电路由组合电路和起记忆作用的存储电路组成,其中存储电路一般由各类触发器组成。
1.8 按其状态的改变方式不同分类
1.8.1 同步时序逻辑电路
- 所有触发器状态的变化是在同一时钟信号作用下同时发生的
1.8.1.1 三组逻辑表达式
输出方程:组合逻辑电路的输出内容
Y = F ( X , Q n ) Y = F(X,Q^n) Y=F(X,Qn)
驱动方程:各个触发器的激励信号
Z = G ( X , Q n ) Z = G(X,Q^n) Z=G(X,Qn)
状态方程:触发器的现态次态
Q n + 1 = H ( X , Q n ) Q^{n+1} = H(X,Q^n) Qn+1=H(X,Qn)
1.8.1.2 按其输入和输出的关系不同
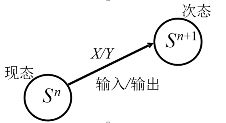
1.8.1.2.1 米里型时序逻辑电路
输出是输入变量和状态变量的函数,输出不仅与输入有关,而且与电路的现态有关
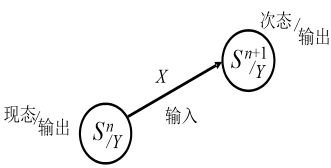
1.8.1.2.2 摩尔型时序逻辑电路
输出只是状态变量的函数,而和当时的输入无关
1.8.2 异步时序逻辑电路
没有统一的时钟信号,各触发器状态的变化不是同时发生的,而是有先有后的
1.9 功能描述方法
1.9.1 逻辑表达式
用于描述时序电路功能的逻辑表达式为输出方程、驱动方程和状态方程。
1.9.2 状态转换表
把时序电路的输入和现态的各种可能取值,代入状态方程和输出方程进行计算,求出相应的次态和输出,将全部的计算结果列成真值表的形式
1.9.3 状态转换图
圆圈:表示时序电路的各种状态。
箭头线:表示状态转换方向
箭头线旁注明:状态转换前的输入变量 X X X的取值和输出变量 Y Y Y的值。
1.9.4 时序图
描述时序电路在输入信号和时钟脉冲序列作用下,电路状态及输出随时间变化的波形图。
1.10 同步时序逻辑电路分析方法
- 列出时序电路的输出方程和各触发器的驱动方程;
- 将触发器的驱动方程代入各自的特性方程,求出各触发器的次态方程,从而得到时序电路的状态方程;
- 根据求得的状态方程和输出方程,列出时序电路的状态转换表;
- 根据状态转换表列出状态表,画出状态图或时序图;
- 总结分析时序电路的逻辑功能。
1.11 自启动能力
电路经过若干个 C L K CLK CLK脉冲作用,还是能进入有效序列,不会陷入某个死循环出不去。
1.12 同步时序逻辑设计
1.12.1 步骤
- 建立原始状态表
- 所要设计的同步时序电路的逻辑功能是通过文字、图形或波形来描述的,首先必须将它们变换成规范的状态图或状态表。这种直接从文字描述得到的状态图或状态表称为原始状态图或原始状态表。
- 状态化简
- 原始状态表(或图)中可能包含多余的状态,消除多余状态的过程称为状态化简。
- 状态编码
- 给最简状态表中的每一个状态指定一个特定的二进制代码,形成编码状态表的过程称为状态编码,也称为状态分配。
- 选择触发器类型
- 确定逻辑方程
- 根据编码状态表和选定触发器类型,写出时序电路的状态方程、驱动方程和输出方程。
- 画逻辑图
- 根据得到的的驱动方程和输出方程,画出逻辑电路图。
- 检查电路是否能自启动,如果不能自启动要重新设计逻辑方程。
- 有些同步时序电路设计中会出现没用的无效状态,当电路上电后可能会进入这些无效而无法退出。
1.12.2 状态化简
设 A A A和 B B B是原始状态表中的两个状态,若分别以 A A A和 B B B为初始状态,加入任意的输入序列,电路均产生相同的输出序列, 即两个状态的转移效果相同,则称 A A A和 B B B是等效状态或等效状态对,记作 ( A , B ) (A, B) (A,B)。凡是相互等效的状态都可以合并成一个状态。
1.12.2.1 判断两个状态是否等效的条件
- 在相同的输入条件下都有相同的输出。
- 在相同的输入条件下次态也等效。 这可能有三种情况
- 次态相同
- 次态交错
- 次态循环(次态互为隐含条件)
1.12.2.2 隐含表法
隐含表是一种斜边为阶梯形的直角三角形表格。该表格两个直角边上的方格数目相等,等于原始状态数减1。隐含表的纵向由上到下、横向从左到右均按照原始状态表中的状态顺序标注,但纵向“缺头”,横向“少尾”。表中的每个小方格用来表示相应的状态对之间是否存在等价关系。如图5-19所示就是根据具有 A A A、 B B B、 C C C、 D D D、 E E E 这五个状态的原始状态表作出的隐含表。
1.12.2.2.1 隐含表化简步骤
- 构造隐含表,并在表中每个方格中标明相应状态对是否等价。
- 状态对肯定不等价的,在隐含表相应方格中标注“×”
- 状态对肯定等价的,在隐含表相应方格中标注“√”
- 状态对条件等价的,在隐含表相应方格中标注等价条件。
- 顺序比较。先将隐含表中所有的状态按照一定顺序对照原始状态表逐一进行比较,并将比较结果按上面的约定标注在隐含表中每一个小方格内。
- 关联比较。追查填有等价条件的那些方格,若发现所填的等价条件肯定不能满足,就在该方格右上角加一个“×”。
- 确定原始状态表的最大等价类。从隐含表的最右边开始,逐列检查各个小方格,凡是未打“×”的方格,都代表一个等价状态对。彼此等价的几个状态可合并到一个等价类中,最终形成若干个最大等价类。如果有的状态没有包含在任何一个最大等价类中,则该状态自己就是一个最大等价类。
5.建立最简状态表。将每个最大等价类用一个状态来代替,将这种替代关系应用于原始状态表,并删除多余行,就得到了最简状态表。
1.12.3 状态编码
建立最简状态表后,要设计的同步时序电路所需的状态数 N N N就被确定下来,进而电路所需要的触发器个数 K K K也被确定下来。
K K K和 N N N应满足下列关系 2 K − 1 ≤ N ≤ 2 K 2^{K-1}\le N \le2^K 2K−1≤N≤2K
状态编码是给最简状态表中用字母表示的 N N N个状态分别指定一个二进制代码的过程,该代码就是这 K K K个触发器的状态组合。
N N N的数目将随着 K K K的增加而急剧增大。在这种情况下,想要对全部编码方案进行一一对比,从中选取最佳方案是十分困难的。因此,在实际工作中常采用经验法,按一定原则进行状态编码,来获得接近最佳的方案。其基本思想是在选择状态编码时,尽可能使状态和输出函数在卡诺图上1单元的分布为相邻,以便形成更大的包围圈。从而有利于状态函数和输出函数的化简。
状态编码依据的原则为:
(1)相同输入条件下,次态相同,现态应给予相邻编码。所谓相邻编码,就是指各二进制代码中只有一位代码不同。
(2)在不同输入条件下的同一现态,次态编码应相邻。
(3)输出相同,现态编码应相邻。