Structured Sequence Modeling With Graph Convolutional Recurrent Networks
https://davidham3.github.io/blog/2018/07/23/structured-sequence-modeling-with-graph-convolutional-recurrent-networks/
Structured Sequence Modeling With Graph Convolutional Recurrent Networks
ICLR 2017(reject),两个模型,第一个是将数据扔到Defferrard的图卷积里面,然后将输出扔到LSTM里面。第二个模型是将RNN中的矩阵乘法换成了图卷积操作,最后对动态的mnist进行了识别。原文链接:Structured Sequence Modeling With Graph Convolutional Recurrent Networks
摘要
GCRN(Graph Convolutional Recurrent Network),一个可以预测结构化序列数据的深度学习模型。GCRN是传统的循环神经网络的在任意的图结构上的一种泛化形式。这样的结构化数据可以表示成视频中的一系列帧,检测器组成的网络监测到的时空监测值,或是用于自然语言建模的词网中的随机游走。我们提出的模型合并了图上的CNN来辨识空间结构,RNN寻找动态模型。我们研究了两种GCRN,对Penn Treebank数据集进行建模。实验显示同时挖掘图的空间与动态信息可以同时提升precision和学习速度。
1 Introduction
很多工作,Donahue et al. 2015; Karpathy & Fei-Fei 2015; Vinyals et al. 2015,利用CNN和RNN的组合来挖掘时空规律性。这些模型那个处理时间变化的视觉输入来做变长的预测。这些网络架构由视觉特征提取的CNN,和一个在CNN后面,用于序列学习的RNN组成。这样的架构成功地用于视频活动识别,图像注释生成以及视频描述。
最近,大家开始对时空序列建模时融合CNN和RNN感兴趣。受到语言模型的启发,Ranzato et al. 2014提出了通过发现时空相关性的能表示复杂变形和动作模式的模型。他们的实验表明在通过quantizing the image patches获得到的visual words上,使用RNN建模,可以很好的预测视频的下一帧以及中间帧。他们的表现最好的模型是recursive CNN(rCNN),对输入和状态同时使用卷积。Shi et al. 2015之后提出了卷积LSTM(convLSTM),一个使用2D卷积利用输入数据的空间相关性,用于时空序列建模的RNN模型。他们成功的对降雨临近预报的雷达回波图的演化进行了预测。
很多重要问题中,空间结构不是简单的网格状。气象站就不是网格状。而且空间结构不一定是空间上的,如社交网络或生物网络。最后,Mikolov et al. 2013等人认为,句子可以解释成在词网上的随机游走,使得我们转向了分析图结构的句子建模问题。
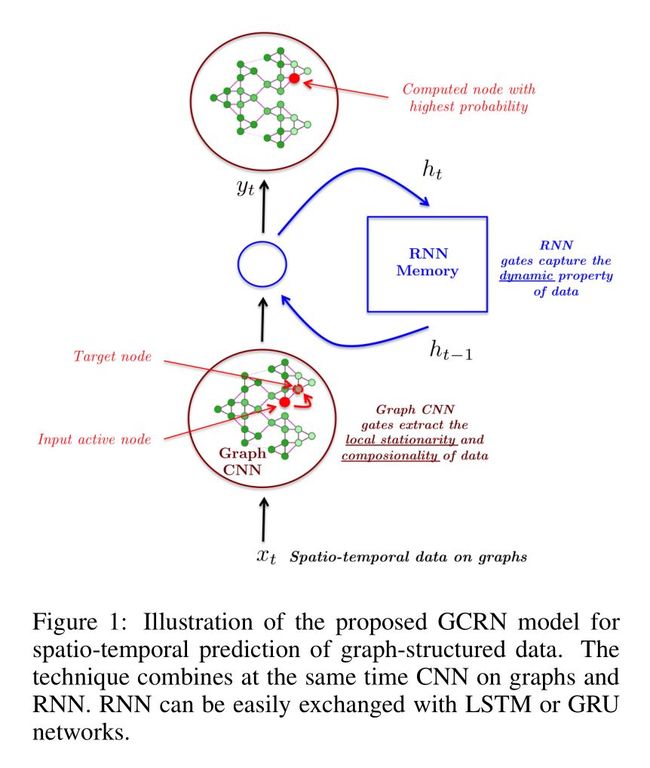
我们的工作利用了近期的模型——Defferrard et al. 2016; Ranzato et al. 2014; Shi et al. 2015——来设计GCRN模型对时间变化的图结构数据建模和预测。核心思想是融合图结构上的CNN和RNN来同时辨识空间结构和动态模式。图1给出了GCRN的架构。
Figure1
2 Preliminaries
2.1 Structured Sequence Modeling
序列建模是给定前JJ个观测值,对未来最可能的长度为KK的序列进行预测:
x^t+1,…,x^t+K=argmaxxt+1,…,xt+KP(xt+1,…,xt+K∣xt−J+1,…,xt),(1)(1)x^t+1,…,x^t+K=argmaxxt+1,…,xt+KP(xt+1,…,xt+K∣xt−J+1,…,xt),
xt∈Dxt∈D是时间tt的观测值,DD表示观测到的特征的域。原型应用是n−gramn−gram模型(n=J+1)(n=J+1),P(xt+1∣xt−J+1,…,xt)P(xt+1∣xt−J+1,…,xt)对在句子中给定过去JJ个词时xt+1xt+1出现的概率进行建模。
我们感兴趣的是特别的结构化的句子,也就是句子中xtxt的特征不是相互独立的,而是有着两两相连的关系。这样的关系广义上通过带权图建模。
xtxt可以看作是一个图信号,也就是一个定义在无向带权图G=(V,ε,A)G=(V,ε,A),其中VV是|V|=n|V|=n个顶点的有限集,εε是边集,A∈Rn×nA∈Rn×n是带权邻接矩阵,编码了两个顶点之间的连接权重。定义在图的顶点上的信号xt:V→Rdxxt:V→Rdx可以当作是一个矩阵xt∈Rn×dxxt∈Rn×dx,列ii是dxdx维向量,表示xtxt在第ii个顶点的值。尽管自由变量的数量在长度为KK的结构化序列中本质上是O(nKdxK)O(nKdxK),我们仍然试图去挖掘可能的预测结果的空间结构以减少维度,来使这些问题变得容易解决。
2.2 Long Short-Term Memory
防止梯度过快消失,由Hochreiter & Schmidhuber 1997发明的一种RNN,LSTM。这个模型已经被证明在各种序列建模任务中,对长期依赖关系是稳定且强劲的模型(Graves, 2013; Srivastava et al., 2015; Sutskever et al., 2014)。全连接LSTM(FC-LSTM)可以看作是一个多变量版本的LSTM,其中xt∈Rdxxt∈Rxd是输入,ht∈[−1,1]dhht∈[−1,1]dh是细胞状态,ct∈Rdhct∈Rdh是隐藏状态,他们都是向量。我们使用Graves 2013的FC-LSTM:
i=σ(Wxixt+Whiht−1+wci⊙ct−1+bi),f=σ(Wxfxt+Whfht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxcxt+Whcht−1+bc),o=σ(Wxoxt+Whoht−1+wco⊙ct+bo),ht=o⊙tanh(ct),(2)(2)i=σ(Wxixt+Whiht−1+wci⊙ct−1+bi),f=σ(Wxfxt+Whfht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxcxt+Whcht−1+bc),o=σ(Wxoxt+Whoht−1+wco⊙ct+bo),ht=o⊙tanh(ct),
其中⊙⊙表示Hadamard product,σ(⋅)σ(⋅)表示sigmoid function σ(x)=1/(1+e−x)σ(x)=1/(1+e−x),i,f,o∈[0,1]dhi,f,o∈[0,1]dh是输入门,遗忘门,输出门。权重Wx⋅∈Rdh×dxWx⋅∈Rdh×dx,Wh⋅∈Rdh×dhWh⋅∈Rdh×dh,wc⋅∈Rdhwc⋅∈Rdh,偏置bi,bf,bc,bo∈Rdhbi,bf,bc,bo∈Rdh是模型参数。这个模型之所以称为全连接是因为Wx⋅Wx⋅和Wh⋅Wh⋅与xx和hh所有分量进行线性组合。由Gers & Schmidhuber 2000引入可选的peephole connections wc⋅⊙ctwc⋅⊙ct,在某些特定任务上可以提升性能。
2.3 Convolutional Neural Networks On Graphs
Defferrard et al., 2016选择了谱上的卷积操作:
y=gθ∗Gx=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx∈Rn×dx,(3)(3)y=gθ∗Gx=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx∈Rn×dx,
对于归一化的拉普拉斯矩阵L=In−D−1/2AD−1/2=UΛUT∈Rn×nL=In−D−1/2AD−1/2=UΛUT∈Rn×n来说,U∈Rn×nU∈Rn×n是矩阵的特征向量,Λ∈Rn×nΛ∈Rn×n是特征值的对角矩阵。式3的时间复杂度很高,因为UU的乘法的时间复杂度是O(n2)O(n2)。此外,计算LL的特征值分解对于大的图来说很慢。Defferrard et al., 2016使用切比雪夫多项式:
gθ(Λ)=∑k=0K−1θkTk(Λ~),(4)(4)gθ(Λ)=∑k=0K−1θkTk(Λ~),
参数θ∈RKθ∈RK是切比雪夫系数的向量,Tk(Λ~)∈Rn×nTk(Λ~)∈Rn×n是切比雪夫多项式的k阶项在Λ~=2Λ/λmax−InΛ~=2Λ/λmax−In的值。图卷积操作可以写为:
y=gθ∗Gx=gθ(L)x=∑k=0K−1θkTk(L~)x,(5)(5)y=gθ∗Gx=gθ(L)x=∑k=0K−1θkTk(L~)x,
T0=1T0=1,T1=xT1=x,Tk(x)=2xTk−1(x)−Tk−2(x)Tk(x)=2xTk−1(x)−Tk−2(x),时间复杂度是O(K|ε|)O(K|ε|),也就是和边数相关。这个图卷积是KK阶局部化的。
3 Related Works
Shi et al. 2015提出了针对常规网格结构的序列的模型,可以看作是图是图像网格且顶点有序的特殊情况。他们的模型本质上是FC-LSTM,WW的乘法替换为卷积核WW:
i=σ(Wxi∗xt+Whi∗ht−1+wci⊙ct−1+bi),f=σ(Wxf∗xt+Whf∗ht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxc∗xt+Whc∗ht−1+bc),o=σ(Wxo∗xt+Who∗ht−1+wco⊙ct+bo),ht=o⊙tanh(ct),(6)(6)i=σ(Wxi∗xt+Whi∗ht−1+wci⊙ct−1+bi),f=σ(Wxf∗xt+Whf∗ht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxc∗xt+Whc∗ht−1+bc),o=σ(Wxo∗xt+Who∗ht−1+wco⊙ct+bo),ht=o⊙tanh(ct),
∗∗表示一组卷积核的2D卷积。在他们的设定中xt∈Rnr×nc×dxxt∈Rnr×nc×dx是一个动态系统中,时间tt的dxdx的观测值,这个动态系统建立在一个表示为nrnr行ncnc列的空间区域上。模型有着空间分布的隐藏核细胞状态,大小是dhdh,由张量ctct体现,ht∈Rnr×nc×dhht∈Rnr×nc×dh。卷积核Wh⋅∈Rm×m×dh×dhWh⋅∈Rm×m×dh×dh和Wx⋅∈Rm×m×dh×dxWx⋅∈Rm×m×dh×dx的尺寸mm决定了参数的数量,与网格大小nr×ncnr×nc无关。更早一点,Ranzato et al. 2014提出了相似的RNN变体,使用卷积层而不是全连接层。时间tt的隐藏状态:
ht=tanh(σ(Wx2∗σ(Wx1∗xt))+σ(Wh∗ht−1)),(7)(7)ht=tanh(σ(Wx2∗σ(Wx1∗xt))+σ(Wh∗ht−1)),
卷积核Wh∈Rdh×dhWh∈Rdh×dh受限到1×11×1的大小。
观察到自然语言表示出语法性质,自然的将词融入短语中,Tai et al. 2015提出了一个处理树结构的模型,每个LSTM可以获取他们的孩子的状态。他们在semantic relatedness and sentiment classification上获得了state-of-the-art的结果。Liang et al. 2016在之后提出了在图上的变体。他们复杂的网络结构在4个数据集上获得了semantic object parsing的state-of-the-art结果。这些模型中,状态通过一个可训练的权重矩阵的带权加和从邻居上聚集。然而这些权重并不在图上共享,否则需要对顶点排序,就像其他图卷积的空间定义一样。此外,他们的公式受限于当前顶点的一阶邻居,给其他的邻居相同的权重。
受到如人体动作和物体交互等时空任务的启发,Jain et al 2016提出了一个方法将时空图看作是一个富RNN的混合,本质上是将一个RNN连接到每个顶点与每条边上。同样的,通信受限于直接连接的顶点与边。
和我们的工作最相关的模型可能是Li et al 2015提出的模型,在program verification上表现出了最好的结果。尽管他们使用Scarselli et al. 2009提出的GNN,以迭代的步骤传播顶点的表示,直到收敛,我们使用的是Defferrard et al. 2016提出的GCN在顶点间扩散信息。尽管他们的动机和我们很不一样,这些模型的关联是使用KK阶多项式定义的谱滤波器可以实现成一个KK层的GNN。
4 Proposed GCRN Models
我们提出了两种GCRN架构
Model 1.
xCNNt=CNNG(xt)i=σ(WxixCNNt+Whiht−1+wci⊙ct−1+bi),f=σ(WxfxCNNt+Whfht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(WxcxCNNt+Whcht−1+bc),o=σ(WxoxCNNt+Whoht−1+wco⊙ct+bo),ht=o⊙tanh(ct).(8)(8)xtCNN=CNNG(xt)i=σ(WxixtCNN+Whiht−1+wci⊙ct−1+bi),f=σ(WxfxtCNN+Whfht−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(WxcxtCNN+Whcht−1+bc),o=σ(WxoxtCNN+Whoht−1+wco⊙ct+bo),ht=o⊙tanh(ct).
我们简单地写成xCNNt=WCNN∗GxtxtCNN=WCNN∗Gxt,其中WCNN∈RK×dx×dxWCNN∈RK×dx×dx是切比雪夫系数。Peepholes由wc⋅∈Rn×dhwc⋅∈Rn×dh控制。这样的架构可能足以捕获数据的分布,通过挖掘局部静止性以及性质的组合性,还有动态属性。
Model 2.
i=σ(Wxi∗Gxt+Whi∗Ght−1+wci⊙ct−1+bi),f=σ(Wxf∗Gxt+Whf∗Ght−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxc∗Gxt+Whc∗Ght−1+bc),o=σ(Wxo∗Gxt+Who∗Ght−1+wco⊙ct+bo),ht=o⊙tanh(ct),(9)(9)i=σ(Wxi∗Gxt+Whi∗Ght−1+wci⊙ct−1+bi),f=σ(Wxf∗Gxt+Whf∗Ght−1+wcf⊙ct−1+bf),ct=ft⊙ct−1+it⊙tanh(Wxc∗Gxt+Whc∗Ght−1+bc),o=σ(Wxo∗Gxt+Who∗Ght−1+wco⊙ct+bo),ht=o⊙tanh(ct),
图卷积核是切比雪夫系数Wh⋅∈RK×dh×dhWh⋅∈RK×dh×dh,Wx⋅∈RK×dh×dxWx⋅∈RK×dh×dx决定了参数的数目,与顶点数nn无关。
这种RNN和CNN的混合,不限于LSTM。普通的RNN ht=tanh(Wxxt+Whht−1)ht=tanh(Wxxt+Whht−1)可以写为:
ht=tanh(Wx∗Gxt+Wh∗Ght−1),(10)(10)ht=tanh(Wx∗Gxt+Wh∗Ght−1),
GRU的版本可以写为:
z=σ(Wxz∗Gxt+Whz∗Ght−1),r=σ(Wxr∗Gxt+Whr∗Ght−1),h~=tanh(Wxh∗Gxt+Whh∗G(r⊙ht−1)),ht=z⊙ht−1+(1−z)⊙h~.(11)(11)z=σ(Wxz∗Gxt+Whz∗Ght−1),r=σ(Wxr∗Gxt+Whr∗Ght−1),h~=tanh(Wxh∗Gxt+Whh∗G(r⊙ht−1)),ht=z⊙ht−1+(1−z)⊙h~.
5 Experiments
Table1
数据集是moving-MNIST(Shi et al., 2015)。
Figure3 & Figure4