RNN-T

RNN-T

1 introduction

许多机器学习任务都可以表示为输入序列到输出序列的转换，如语音识别、机器翻译等。序列转换的关键挑战之一是用一种不会扭曲序列的方式来表示输入和输出序列，比如收缩、拉伸和翻译等。Recurrent neural networks(RNNs)就具备这样的表示能力。但是，RNNs需要提前知道输入序列和输出序列的alignment才能进行转换，这在语音识别中是一件很难的事情，人工标注哪一帧语音对应哪一个输出标签不现实。事实上，即便知道输出序列的长度也是充满挑战性的。RNN-T是一种基于RNN的端到端序列转换系统，它能够将任何input sequence转换成任何有限长output sequence。

设输入序列$x=(x_1,x_2,...,x_T)$ ，输出序列$y=(y_1,y_2,...,y_U)$. 输入向量 $x_t$和输出向量$y_u$都是固定长的实值向量。比如$x_t$是MFC参数的一个向量，$y_u$是一个输出字符的one-hot编码向量。

整个模型框架如下:

$Y$是输出空间(即建模单元集)
$\bar{Y}$是扩充后的输出空间，具体表现为$\bar{Y}=Y\cup \varnothing$。$\varnothing$表示输出为空。(即加上blank后的建模单元集)
$Y^{\ast }$：在输出空间Y上的所有序列组成的集合
${\bar{Y}}^{\ast }$：扩充后的所有输出可能路径集合

比如，$a=(y_1,\varnothing ,\varnothing ,y_2,\varnothing ,y_3)\in {\bar{Y}}^{\ast }$, 即等价于$y=(y_1,y_2,y_3)\in Y^{\ast }$. 我们把 $a\in {\bar{Y}}^{\ast }$称为一个对齐，空输出的位置决定了输入和输出是如何对齐的。这样的$a$有很多种可能，我们需要一一罗列出这样符合条件的路径。其概率和就是给定input sequence下生成Y的概率。
$P(y\in Y^{\ast }|x)=\sum _{a\in {\pi }^{-1}(y)}P(a|x)$
其中，$\pi :{\bar{Y}}^{\ast }\to Y^{\ast }$, 表示把扩充后的路径去除空输出得到真实路径。

我们用俩个神经网络来计算$P(a|x)$。一个被称为转录网络(transcription network)$F$, 其作用是将输入序列$x$转换成输出向量序列$f=(f_1,f_2,...,f_T)$. 另外一个称为预测网络(prediction network)$G$,其作用是由标注序列$y$输出预测向量序列$g=(g_0,g_1,...,g_U)$

2.1 prediction network

预测网络$G$的输入是长为$U+1$的序列$y^{\ast }=(\varnothing ,y_1,...,y_U)$,其在标注序列$y$前面加了一个$\varnothing$。如果建模单元集$Y$包括$K$个建模单元，那么输入层的大小就是$K$. $\varnothing$编码为长$K$的零向量。输出层大小为$K+1$, 对应加上blank后的建模单元集$\bar{Y}$，因此预测向量$g_u$大小也是$K+1$.
给定$y^{\ast }$, $G$输出hidden sequence$(h_0,h_1,...,h_U)$和outtput sequence$(g_0,g_1,...,g_U)$. 通过从$u=0$到$U$迭代以下方程:

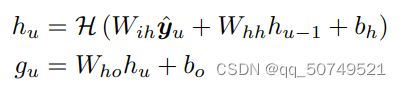
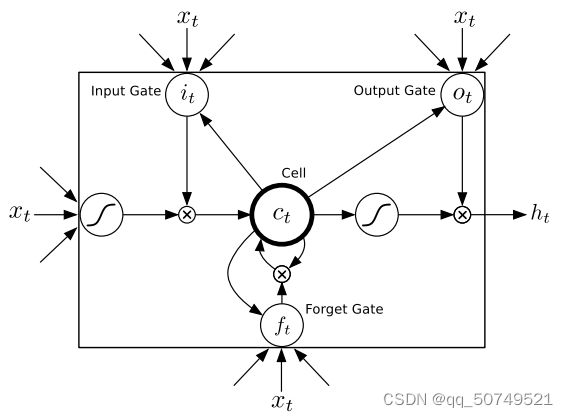
其中, $W_{ih}是input-hidden$的权重矩阵，$W_{hh}是hidden-hidden$的权重矩阵，$W_{ho}$是$hidden-output$的权重矩阵。$b_h$和$b_o$是偏置矩阵。在传统的RNN中，$H$这个隐层函数一般就是$tanh$或者$sigmoid$，但我们发现LSTM更能利用上下文信息。这篇文章里LSTM的参数是包括一下复合函数：

预测网络试图在给定前一个标注的条件下，建模$y$中的每个元素。因此类似语言模型，唯一的区别是多了空符号预测。

2.2 Transcription network

这个网络和CTC里的encoder网络是一个事情。
给定长度为$T$的输入序列$(x_1,x_2,...,x_T)$，该网络输出等长的隐向量序列$(f_1,f_2,...,f_T)$,其中每个向量大小为$K+1$.
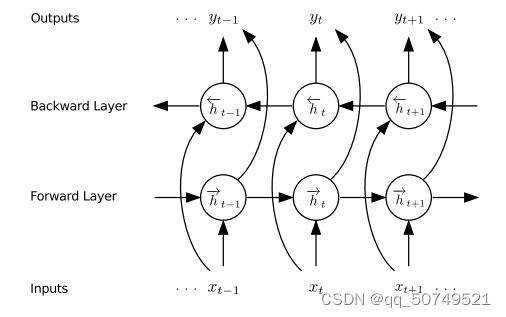
这里用的是一个双向RNN，从前到后、从后到前会有俩个hidden layer,他们会前馈到同一个输出层中。不用于传统单向RNN只考虑previous inputs，双向RNN会考虑未来的信息，效果往往更好。
输入input:$(x_1,x_2,...,x_T)$
输出: forward hidden sequence $(\overrightarrow{h_1},\overrightarrow{h_2},...,\overrightarrow{h_T})$
backward hidden sequence :$(\overleftarrow{h_1},\overleftarrow{h_2},...,\overleftarrow{h_T})$
output layer:$(f_1,f_2,...,f_T)$
这里同样是用一个双向的LSTM network：
从$t=T$到1迭代 backward layer:

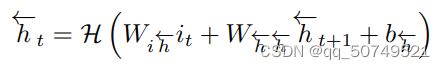
从$t=1$到T迭代 forward layer:

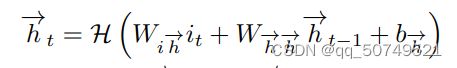
最终把forward layer和backward layer都前馈到同一个Output layer里：

参数$H$和prediction network里是一样的。双向RNN结构如下：

2.3 output distribution

在上面的prediction network中，我们输入上一个标签$y_{u-1}$,去预测下一个标签$y_u$，相当于语言模型。每个$y_u$都是一个大小为$K+1$的向量，对应$K+1$个建模单元。在上面的transription network中，我们是对输入序列做了encode，相当于声学模型。得到$(f_1,f_2,..,f_T)$, 每个$f_t$也都是大小为$K+1$的向量。
现在我们要把他们拼接在一起，也就是第一张图中的joint network。一般的话
就是两者直接相加，也可以赋予不同的权重。

给定转录网络输出向量$f_t$,其中$1\le t\le T$。预测网络输出向量$g_u$,其中$1\le u\le U$, 以及标注$k\in \bar{Y}$. 两者拼接起来得到:
$h_{t,u}=f_t+g_u$
因为$f_t$和$g_u$都是$K+1$维向量，所以$h_{t,u}$也是$K+1$维向量。进一步，我们做softmax，得到一个distribution:
$P(k|t,u)=\frac{e^{h(k,t,u)}}{\sum _{k^{\prime }\in \stackrel{-}{Y}}{e}^{h(k^{\prime },t,u)}}$
这个distribution是一个$K+1$维的概率分布。表示对应输出建模单元集中第k个建模单元的概率。

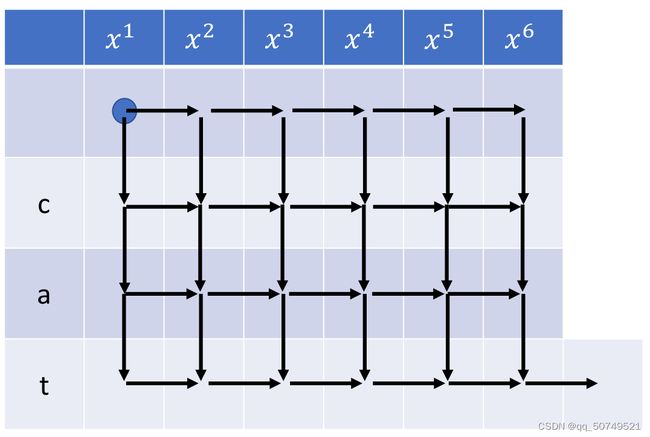
前面我们说到，假如对于一个长为6语音样本$x=(x_1,x_2,x_3,x_4,x_5,x_6)$，文本$y$是$cat$. 我们训练的目标就是为了优化模型参数，使得在给定输入序列$x$的时候，最大化输出概率$P(y|x)$。
而在RNN-T当中，我们需要找到所有可能路径$\stackrel{\wedge }{y}$,其可能情况有这样很多种, 我们拿其中一条来举例，看看他是怎么做alignment的。

如下所示，x1输出blank，表示未提取到有用信息，走到x2，x2输出c这个token之后，没有更多有用信息了，就接着输出blank，并走到x3。x3没有有效信息，输出blank走到x4。 x4输出a后没有更多有效信息，接着输出blank到x5。x5输出t后没有更多有效信息，接着输出blank到x6。注意在x6处还需输出一个blank，表示x6的信息也已经提取结束，整个句子信息提取完成。

整个路径为$(\varnothing ,c,\varnothing ,\varnothing ,a,\varnothing ,t,\varnothing ,\varnothing )$

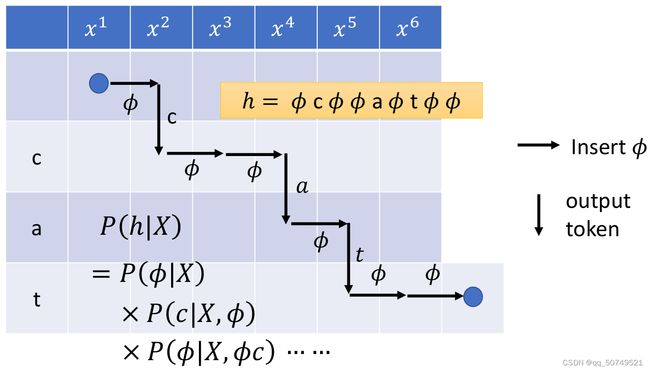
我们可以总结一下几点：

1. 整个alignment路径的长度是$T+U$, 在这里就是6+3=9
2. 对于每个时刻的输入$x_t$, 如果所有信息全部提取结束，就一定会输出一个blank。要注意的是，一个$x_t$不一定只输出一个token再blank，也可以同时输出多个token后再blank。
3. 不同于CTC每时刻的输出只依赖于当前输入特征$x_t$, RNN-T不仅依赖于$x_t$,同时依赖上一个预测标签$y_u$。这一块prediction network完成的工作相当于语言模型，也就完善了CTC输出独立的问题，从而RNN-T有更好的performance。

像这样，我们找到这样所有满足条件的路径后，概率相加就能得到输出概率:
$P(y|x)=\sum _{\stackrel{\wedge }{y}\in A_{RNN-T}(x,y)}P(\stackrel{\wedge }{y}|x)$
而每一条路径$\stackrel{\wedge }{y}$的概率，如上面这条路径的概率:
$P(\varnothing ,c,\varnothing ,\varnothing ,a,\varnothing ,t,\varnothing ,\varnothing )=P(\varnothing |x_1)P(c|x_2,\varnothing )P(\varnothing |x_2,\varnothing c)....P(\varnothing |x_6,\varnothing c\varnothing \varnothing a\varnothing t\varnothing )$

训练的时候，对于标注$y$, 我们都需要找到所有满足条件的对齐路径，这样才能够得到输出概率$P(y|x)$,从而进一步优化模型参数，使得这个概率最大。
很显然，这是很费劲的。为了进行训练，我们同样引入了forward-backward算法来计算概率。

2.4 Forward-Backward Algorithm

定义前向概率$\alpha (t,u)$, 表示在$f_{[1:t]}$期间输出$y_{[1:u]}$的概率。下图是由$P(k|t,u)$定义的输出概率词图。位于$(t,u)$处的节点表示在转录序列的$t$时刻，输出目标序列前$u$个元素的概率。

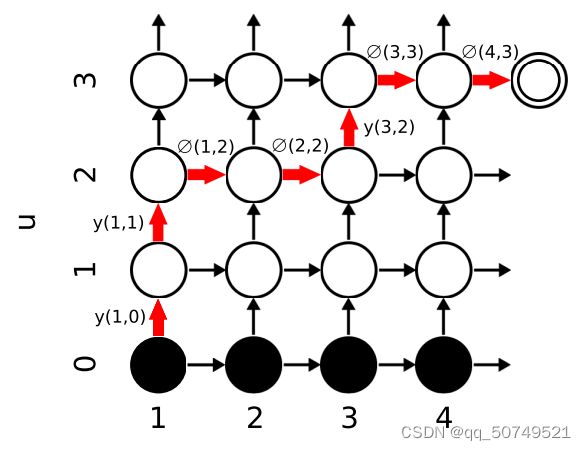
如上图所示，一开始处在(1,0)位置，并初始化$\alpha (1,0)=0$。
下面开始转移，我们可以有两条路走，一方面水平向右走，表示这个$f_t$已经提取完信息了，输出一个blank。另一方面，垂直向上走，表示这个$f_t$输出了一个token。
所以，为了方便表示，我们把输出分为俩部分：token or blank。定义如下两个概率：
$y(t,u)=P(y_{u+1}|t,u)$表示在$(t,u)$处向上走，输出token $y_{u+1}$
$\varnothing (t,u)=P(\varnothing |t,u)$表示在$(t,u)$处向右走，输出blank。

于是，通过迭代计算，走到每个位置$(t,u)$的累积概率$\alpha (t,u)$如下：

一直走到$(T,U)$最后一个位置，要注意的是，这个时候还需要输出一个blank，表示$f_T$的信息已经提取完成，整个句子也就走完了。从而，输出概率可以表示为:

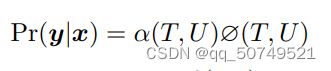
从左下到右上终止节点的所有路径对应输入输出序列间可能的对齐(alignment)
类似的，我们定义后向概率$\beta (t,u)$在$f_{t:T}$期间输出$y_{[u+1:U]}$的概率，从而:

其初始条件为$\beta (T,U)=\varnothing (T,U)$.

从前后向概率的定义可以得出，它们在输出词图上任意点$(t,u)$的乘积$\alpha (t,u)\beta (t,u)$等于在转录时刻$t$输出$y_u$的条件下，输出完整标注序列的总概率。

补充，在上面$cat$这个例子中，整个词图网络如下：

2.5 Training

给定输入序列$x$，目标序列$y$。训练的目标就是为了最大化输出概率$P(y|x)$, 也就是最小化损失函数$-lnP(y|x)$. 分析输出词图上概率的分布，可见$P(y|x)$等于$\alpha (t,u)\beta (t,u)$, 在任意从左下到右上对角线所经过节点的和，即:

得到loss之后，进一步反向传播，更新参数。

2.6 Testing

给定X, 解码目标就是找到概率最大的目标序列$Y^{\ast }$:
$Y^{\ast }=\underset{Y}{\mathrm{argmax}}P(Y|X)=\underset{Y}{\mathrm{argmax}}\sum _{\stackrel{\wedge }{y}}P(\stackrel{\wedge }{y}|X)$
如果罗列出所有可能路径，再一一转成目标序列，比较概率大小，是非常麻烦的。
如果用prefix-search decoding解码方式，也就是每时刻找到输出概率最大的那个，最后得到目标序列。
但这样一条最大概率路径并不一定是最优解，这是因为，我们最终的目标序列可能会有很多条路径概率相加，这多条路径的概率加起来会比最大概率的那一条路径概率更大。
所以我们一般会用beam search找出n-best。
简单来说，$t_1$时刻，找出$P(k|1,0)$的三个最大值，以此为节点，$t_2$时刻继续向下扩展，每次都找出3-best，一直走到最后。

3 Reference：

http://www.cs.toronto.edu/~fritz/absps/RNN13.pdf
https://arxiv.org/pdf/1211.3711.pdf