- 百度地图开放平台Key值申请
前端熊猫
百度地图开发平台AK
百度地图开放平台key值获取流程首先,登录需选择个人或者企业实名认证进入百度地图开放平台,点击右上角的控制台,进入开发者管理界面:选择应用管理->我的应用,点击创建应用,填写服务端:需设置IP白名单(安全性更高)或者浏览器端:需配置Referer白名单(防止恶意调用),获取测试key!!!在“我的应用”列表中,可查看并复制AK
- 学习Video.js
前端熊猫
VideoPlayer学习
查阅官方文档,学习video.js相关属性、回调与方法:播放器选项设置①标准的video标签属性②data-setup属性传递JSON③创建播放器实例以第二个参数配置videojs('my-player',{controls:true,autoplay:false,preload:'auto'});//修改选项varplayer=videojs('my-player');player.option
- 神经网络中层与层之间的关联
iisugar
神经网络深度学习计算机视觉
目录1.层与层之间的核心关联:数据流动与参数传递1.1数据流动(ForwardPropagation)1.2参数传递(BackwardPropagation)2.常见层与层之间的关联模式2.1典型全连接网络(如手写数字分类)2.2卷积神经网络(CNN,如图像分类)2.3循环神经网络(RNN/LSTM,如文本生成)2.4Transformer(如机器翻译)3.层间关联的核心原则3.1数据传递的“管道
- 第二十一篇:伦理/道德Ethics
flying_1314
NLPethics伦理/道德隐私偏见双重用途
目录什么是伦理/道德?我们为什么要关心?为什么道德很难?学习成果大纲反对NLP道德检查的论据我们应该审查科学吗?H5N1透明度不是更好吗?AIvs.Cybersecurity核心NLP伦理概念偏见词嵌入中的偏差双重用途OpenAIGPT-2隐私GDPRAOL搜索数据泄露小组讨论提示自动刑期预测自动简历处理语言社区分类打包带走~什么是伦理/道德?我们应该如何生活——苏格拉底•正确的做法是什么?•为什
- 【STM32】智能避障红外小车
Alioooooooon
嵌入式stm32单片机嵌入式硬件
文章目录直流电机`motor.c/motor.h`红外对管红外循迹利用脉冲宽度调制技术(PWM)控制电机转速避障`red.c/red.h`编译环境:keil5SourceInsightSTM32F103X原理图:直流电机直流电机的原理:通电就会转,反向通电就会反转两极的电势差决定转速电机驱动模块以及接线参考图示代码实现:motor.c/motor.h#ifndef__MOTOR_H__#defin
- 前端请求怎么发送到后端:深度剖析与实用指南
dhfnngte24fhfn
pythondjangopygamevirtualenv
前端请求怎么发送到后端:深度剖析与实用指南在web开发中,前端与后端之间的通信是至关重要的。前端通过发送请求来获取后端的数据或执行某些操作,而后端则负责处理这些请求并返回相应的响应。本文将分四个方面、五个方面、六个方面和七个方面,深入剖析前端请求是如何发送到后端的,并为你提供实用的指南。四个方面:请求与响应的基础首先,我们需要了解前端请求与后端响应的基础概念。前端通过HTTP协议向后端发送请求,后
- SAP-ABAP:SAP生产业务(PP模块)全流程深度解析
爱喝水的鱼丶
VIP详情查看专栏SAPABAP开发运维运维系统架构
SAP生产业务(PP模块)全流程深度解析一、生产主数据架构体系1.主数据矩阵物料主数据工艺路线工作中心生产版本MRP运行2.核心主数据表数据对象表结构关键字段事务码物料主数据MARAMATNR,MTART,DISMMMM01工艺路线PLKO/PLPOPLNNR(路由号),VORNR(工序)CA01工作中心CRHD/CRTXARBPL(工作中心),KAPAR(能力)CR01BOMMAST/STPOS
- 运维面试题(七)
a_j58
运维
1.statefulset用来管理有状态的应用程序,有状态是什么意思?每一个pod都有一个固定的网络标识符,在整个生命周期中不会改变。每个实例都可以拥有自己的持久化存储卷,即使容器被删除并重新创建,存储卷仍然存在。StatefulSet确保了Pod按照顺序启动、更新和终止。2.主键是什么,它与索引有什么关系?主键确保表中每一行数据都可以被唯一标识,避免数据重复。主键通常会自动创建一个唯一索引,加快
- 谈谈互联网后端基础设施
GarfieldEr007
JavaWeb互联网后端基础设施web
本文更新于2016.12.06,加入了Netflix组件部分对于一个互联网企业,后端服务是必不可少的一个组成部分。抛开业务应用来说,往下的基础服务设施做到哪些才能够保证业务的稳定可靠、易维护、高可用呢?纵观整个互联网技术体系再结合公司的目前状况,个人认为必不可少或者非常关键的后端基础技术/设施如下图所示:这里的后端基础设施主要指的是应用在线上稳定运行需要依赖的关键组件/服务等。开发或者搭建好以上的
- css filter属性详解
pengfeixc
CSScsscss3webdevelopment
cssfilter属性详解文章中codepen例子,无法实时预览,可以在这里获得更好阅读体验。最近琢磨着把网站主题色更改一下,看到了一篇文章DarkModeinOneLineofCode,作者讲述了如何用一句代码将网站主题色更改成相反色,这样网站就可以拥有有白天模式和黑夜模式了。html{filter:invert(1);}使用上面的代码,可以很方便的将页面颜色反转,达到黑夜模式的效果。但是我并不
- 深夜惊魂:当监控告警“撒谎”时,SRE 如何逆风翻盘?
YAMLMaster
kubernetes运维开发devops容器云原生
Yorkshire,England引言我们这一篇也是含金量十足,如果面试官让你说个你处理过的比较有意思的案例,可以跟他讲讲,让他也见见世面。好吧,我们直接开始,最后有相关的群,有兴趣可以加入。开始一、故障场景深度还原时间:2025年1月3日02:00(GMT+8)环境:•数据库集群:MySQL8.0.35,通过KubeBlocks部署(3节点,跨AZ)•监控架构:•Prometheus-Opera
- 云原生工程师必修课:如何揪出“假忙真闲”的应用元凶
YAMLMaster
面试题kubernetes运维开发devops
Tagamanent,Spain引言这是一个再经典不过的面试题了,希望大家能学到精髓。开始介绍在分布式系统和高并发场景中,高负载(HighLoad)与低使用率(LowUtilization)的共存矛盾是运维和开发者的常见挑战。这种问题往往隐蔽性强,传统监控指标难以直接定位根因。本文从系统层、应用层、架构层多维度拆解,提供一套完整的排查与优化方法论。核心概念厘清•负载(Load):系统当前待处理任务
- 动作捕捉手套如何让虚拟现实人机交互 “触手可及”?
广州虚拟动力-动捕&虚拟主播
VR手套数据手套动捕手套动捕数据手套
在虚拟与现实逐渐交融的当下,动作捕捉技术正以前所未有的速度革新着多个领域。动作捕捉技术,简称“动捕”,已经从早期的影视特效制作,逐步拓展到游戏开发、虚拟现实、机器人控制等多个领域。而mHandPrO数据手套作为这一领域的新兴力量,正以其实时、精准的动作捕捉能力,为用户带来全新的交互体验。其内置的感应节点、震动器和反馈装置,能够精准捕捉手部的细微动作,并实时转化为虚拟空间中的自然、流畅互动。在VR娱
- Pytorch深度学习教程_9_nn模块构建神经网络
tRNA做科研
深度学习保姆教程深度学习pytorch神经网络
欢迎来到《深度学习保姆教程》系列的第九篇!在前面的几篇中,我们已经介绍了Python、numpy及pytorch的基本使用,进行了梯度及神经网络的实践并学习了激活函数和激活函数,在上一个教程中我们学习了优化算法。今天,我们将开始使用pytorch构建我们自己的神经网络。欢迎订阅专栏进行系统学习:深度学习保姆教程_tRNA做科研的博客-CSDN博客目录1.理解nn模块:(1)使用nn.Sequent
- 【MyBatisPlus】MyBatisPlus介绍与使用
web_15534274656
面试学习路线阿里巴巴java
【MyBatisPlus】MyBatisPlus介绍与使用文章目录【MyBatisPlus】MyBatisPlus介绍与使用1、什么MyBatisPlus2、MyBatisPlus的CRUD操作3、MyBatisPlus分页使用1、什么MyBatisPlusMyBatisPlus(简称MP)是基于MyBatis框架基础上开发的增强型工具,旨在简化开发、提高效率官网:https://baomidou
- k8s运维 设置Pod实现JVM内存根据容器内存动态调整
风行無痕
K8Skubernetesjvm容器
一、实现方式推荐方案:利用JVM容器感知特性,按比例动态分配。适用场景:动态根据Pod内存限制自动分配堆内存,无需硬编码参数Java要求:Java8u191+或Java11+Java8u191+或Java11+支持通过-XX:InitialRAMPercentage替代-Xms,根据容器内存限制自动计算堆内存。在容器环境变量中配置-XX:MaxRAMPercentage=75.0,使JVM根据容
- SAP-ABAP:ABAP内存和SAP内存详细对比
爱喝水的鱼丶
VIP详情查看专栏SAP-ABAP开发基础详解ABAP开发之必须知道的SAP运维ABAPERP
在SAPABAP中,内存数据(MemoryData)是一种临时存储机制,允许在同一会话或程序之间共享数据。内存数据存储在ABAP内存(ABAPMemory)或SAP内存(SAPMemory)中,具体取决于数据的生命周期和共享范围。以下是关于如何在SAP中保存和使用内存数据的详细说明:—##1.ABAP内存vsSAP内存###ABAP内存-作用范围:仅在当前内部会话(InternalSession)
- 【机器学习】算法分类
CH3_CH2_CHO
什么?!是机器学习!!机器学习算法有监督学习无监督学习半监督学习强化学习
1、有监督学习1.1定义使用带标签的数据训练模型。有监督学习是机器学习中最常见的一种类型,它利用已知的输入特征和对应的输出标签来训练模型,使模型能够学习到特征与标签之间的映射关系。在训练过程中,模型会不断地调整自身的参数,以最小化预测值与真实标签之间的误差,从而提高预测的准确性。1.2回归问题1.2.1目标预测连续值。回归问题的目标是预测一个连续的数值结果,模型的输出是一个实数值。1.2.2解释回
- 基于Redis分布锁+事务补偿解决数据不一致性问题
yiridancan
并发编程Redis分布式redis数据库缓存
基于Redis的分布式设备库存服务设计与实现概述本文介绍一个基于Redis实现的分布式设备库存服务方案,通过分布式锁、重试机制和事务补偿等关键技术,保证在并发场景下库存操作的原子性和一致性。该方案适用于物联网设备管理、分布式资源调度等场景。代码实现importjava.util.HashMap;importjava.util.Map;importorg.slf4j.Logger;importorg
- Linux------Redis(软件安装,Linux下和Windows下),NoSQL(简单了解)
.墨迹.
Linuxredis大数据java
文章目录NoSql1.历史1.单机MySql2.Memcached(缓存)+MySql+垂直拆分(读写分离)3.分库分表+水平拆分+MySql集群4.如今最近的年代5.为什么要使用NoSQL2.什么是NoSQL1.NOSQL2.特点3.3v+3高3.NoSQL的四大分类1.kv键值对:2.文档型数据库(bson和json一样):3.列存储数据库:4.图关系型数据库Redis1.初始redis1.简
- Python 单例模式的 5 种实现方式:深入解析与最佳实践
做测试的小薄
测试高阶python单例模式自动化测试测试框架
单例模式(SingletonPattern)是一种经典的设计模式,其核心思想是确保一个类在整个程序运行期间只有一个实例,并提供一个全局访问点。这种模式在许多场景中非常有用,例如全局配置管理、日志记录器、数据库连接池等。然而,Python的灵活性使得实现单例模式有多种方式,每种方法都有其特点和适用场景。本文将详细介绍Python中实现单例模式的5种常见方法,并深入分析它们的优缺点以及适用场景,帮助您
- MySQL密码修改的全部方式一篇详解
1加1等于
MySQLmysql数据库
本文将详细介绍多种修改MySQL密码的方式。本文目录一、alteruser语句操作步骤二、setpassword操作步骤三、直接修改mysql.user表操作步骤一、alteruser语句当你以root用户或者拥有足够权限的用户登录MySQL时,可以使用ALTERUSER语句来修改密码。这种方式适用于MySQL5.7及以上版本,简单直接,且符合MySQL的标准操作规范。操作步骤首先,使用以下命令登
- Java并发实战——CountDownLatch优化商品详情页数据加载
1加1等于
Java并发java开发语言多线程
本文将结合电商场景比如优化商品详情页数据加载,深入探讨CountDownLatch的工作原理及实际应用。本文目录1.简介2.商品详情页数据加载优化实战3.CountDownLatch的优势4.其他应用场景5.使用误区1.简介CountDownLatch是Java并发包java.util.concurrent中的一个同步工具类。允许一个或多个线程等待,直到其他一组线程完成一系列操作。CountDow
- Java进阶——常用类及常用方法详解
1加1等于
Javajava
本文将深入探讨Java常用类的核心知识点以及在日常工作中的使用场景。本文目录一、String类1.不可变性2.字符串常量池3.比较字符串二、日期时间常用类1.Java8引入2.时间计算三、Math数值处理四、Optional空值处理五、异常处理类六、枚举类一、String类1.不可变性String类是不可变的,这意味着一旦创建就不能被修改。在进行字符串拼接时,需要注意性能问题。//不推荐:会创建多
- Java进阶——数组超详细整理
1加1等于
Javajava数据结构
数组是一种基础且重要的数据结构,广泛应用于各种场景,本文将深入探讨Java数组的相关知识点,并结合实际场景展示其应用。本文目录一、数组声明与初始化1.声明方式2.初始化方法3.长度特性二、内存管理三、数组遍历与操作1.遍历方式2.数组填充四、多维数组五、数组工具类Arrays六、数组与集合的转换1.数组转集合2.集合转数组总结一、数组声明与初始化1.声明方式数组的声明有两种方式:int[]prod
- SpringBoot + Facade Pattern : 通过统一接口简化多模块业务
Java布道者
springboot外观模式后端
概述外观设计模式(FacadePattern)是一种常见的结构型设计模式,它的主要目的是简化复杂系统的使用。可以把它想象成一个“控制面板”或者“遥控器”,通过这个控制面板,用户可以轻松操作一个复杂的系统,而不需要关心系统内部是如何运作的。举个生活中的例子,想象一下,你家有一台多功能的家电,比如一台智能电视,它不仅能看电视,还能上网、播放视频、控制智能家居等等。对于电视的操作,你有遥控器,可以通过一
- P2P通信:WebRTC的原理与实现
幻想彩虹中的绚丽光华
p2pwebrtc网络协议WebRTC
WebRTC(WebReal-TimeCommunication)是一种用于在Web浏览器之间进行实时通信的开放标准。它提供了一种直接的点对点(P2P)通信方式,使得浏览器之间可以实时传输音频、视频和数据。本文将详细介绍WebRTC的原理和实现,并提供相应的源代码示例。WebRTC的原理:WebRTC利用了多种技术,包括实时传输协议(RTP)、会话发起协议(SDP)、媒体传输控制协议(RTCP)和
- 删除 mkcert 根证书
堕落年代
杂论网络
1.删除mkcert根证书(关键步骤)Windows系统打开证书管理器:•按Win+R,输入certmgr.msc,回车。定位根证书:•左侧导航栏依次展开受信任的根证书颁发机构→证书。•在右侧列表中找到mkcert@或mkcertdevelopmentCA。删除证书:•右键证书→删除→确认操作。macOS系统打开钥匙串访问:•通过Spotlight搜索或进入应用程序/实用工具。定位根证书:•左侧选
- Ruoyi报‘com.ruoyi.system.api.RemoteLogService‘ that could not be found.
堕落年代
SpringCloudSpringbootspringcloudspringboot
解释这个因为在引包的时候有些包的配置没有导入进去,想要解决这个问题最简单的方式就是注释掉这个的包的导入。解决方法报错***************************APPLICATIONFAILEDTOSTART***************************Description:FieldremoteLogServiceincom.ruoyi.common.log.service.
- 一些工程实践中的tips
litvm
经验分享经验分享
1,简单方法实现四舍五入实际项目中,经常会出现需要四舍五入的地方,比如采集温度temp,如果直接把float类型保存为小数点后1位。它会直接舍后面多余的位数,这样可能偏差会比较大。我们可以通过+0.5来实现四舍五入。比如:floattemp=30.6;//假设我们是扩大10倍保存//直接保存uint16_tmodbus_data.temp=temp*10;//结果就是30//+0.5uint16_
- ztree设置禁用节点
3213213333332132
JavaScriptztreejsonsetDisabledNodeAjax
ztree设置禁用节点的时候注意,当使用ajax后台请求数据,必须要设置为同步获取数据,否者会获取不到节点对象,导致设置禁用没有效果。
$(function(){
showTree();
setDisabledNode();
});
- JVM patch by Taobao
bookjovi
javaHotSpot
在网上无意中看到淘宝提交的hotspot patch,共四个,有意思,记录一下。
7050685:jsdbproc64.sh has a typo in the package name
7058036:FieldsAllocationStyle=2 does not work in 32-bit VM
7060619:C1 should respect inline and
- 将session存储到数据库中
dcj3sjt126com
sqlPHPsession
CREATE TABLE sessions (
id CHAR(32) NOT NULL,
data TEXT,
last_accessed TIMESTAMP NOT NULL,
PRIMARY KEY (id)
);
<?php
/**
* Created by PhpStorm.
* User: michaeldu
* Date
- Vector
171815164
vector
public Vector<CartProduct> delCart(Vector<CartProduct> cart, String id) {
for (int i = 0; i < cart.size(); i++) {
if (cart.get(i).getId().equals(id)) {
cart.remove(i);
- 各连接池配置参数比较
g21121
连接池
排版真心费劲,大家凑合看下吧,见谅~
Druid
DBCP
C3P0
Proxool
数据库用户名称 Username Username User
数据库密码 Password Password Password
驱动名
- [简单]mybatis insert语句添加动态字段
53873039oycg
mybatis
mysql数据库,id自增,配置如下:
<insert id="saveTestTb" useGeneratedKeys="true" keyProperty="id"
parameterType=&
- struts2拦截器配置
云端月影
struts2拦截器
struts2拦截器interceptor的三种配置方法
方法1. 普通配置法
<struts>
<package name="struts2" extends="struts-default">
&
- IE中页面不居中,火狐谷歌等正常
aijuans
IE中页面不居中
问题是首页在火狐、谷歌、所有IE中正常显示,列表页的页面在火狐谷歌中正常,在IE6、7、8中都不中,觉得可能那个地方设置的让IE系列都不认识,仔细查看后发现,列表页中没写HTML模板部分没有添加DTD定义,就是<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3
- String,int,Integer,char 几个类型常见转换
antonyup_2006
htmlsql.net
如何将字串 String 转换成整数 int?
int i = Integer.valueOf(my_str).intValue();
int i=Integer.parseInt(str);
如何将字串 String 转换成Integer ?
Integer integer=Integer.valueOf(str);
如何将整数 int 转换成字串 String ?
1.
- PL/SQL的游标类型
百合不是茶
显示游标(静态游标)隐式游标游标的更新和删除%rowtyperef游标(动态游标)
游标是oracle中的一个结果集,用于存放查询的结果;
PL/SQL中游标的声明;
1,声明游标
2,打开游标(默认是关闭的);
3,提取数据
4,关闭游标
注意的要点:游标必须声明在declare中,使用open打开游标,fetch取游标中的数据,close关闭游标
隐式游标:主要是对DML数据的操作隐
- JUnit4中@AfterClass @BeforeClass @after @before的区别对比
bijian1013
JUnit4单元测试
一.基础知识
JUnit4使用Java5中的注解(annotation),以下是JUnit4常用的几个annotation: @Before:初始化方法 对于每一个测试方法都要执行一次(注意与BeforeClass区别,后者是对于所有方法执行一次)@After:释放资源 对于每一个测试方法都要执行一次(注意与AfterClass区别,后者是对于所有方法执行一次
- 精通Oracle10编程SQL(12)开发包
bijian1013
oracle数据库plsql
/*
*开发包
*包用于逻辑组合相关的PL/SQL类型(例如TABLE类型和RECORD类型)、PL/SQL项(例如游标和游标变量)和PL/SQL子程序(例如过程和函数)
*/
--包用于逻辑组合相关的PL/SQL类型、项和子程序,它由包规范和包体两部分组成
--建立包规范:包规范实际是包与应用程序之间的接口,它用于定义包的公用组件,包括常量、变量、游标、过程和函数等
--在包规
- 【EhCache二】ehcache.xml配置详解
bit1129
ehcache.xml
在ehcache官网上找了多次,终于找到ehcache.xml配置元素和属性的含义说明文档了,这个文档包含在ehcache.xml的注释中!
ehcache.xml : http://ehcache.org/ehcache.xml
ehcache.xsd : http://ehcache.org/ehcache.xsd
ehcache配置文件的根元素是ehcahe
ehcac
- java.lang.ClassNotFoundException: org.springframework.web.context.ContextLoaderL
白糖_
javaeclipsespringtomcatWeb
今天学习spring+cxf的时候遇到一个问题:在web.xml中配置了spring的上下文监听器:
<listener>
<listener-class>org.springframework.web.context.ContextLoaderListener</listener-class>
</listener>
随后启动
- angular.element
boyitech
AngularJSAngularJS APIangular.element
angular.element
描述: 包裹着一部分DOM element或者是HTML字符串,把它作为一个jQuery元素来处理。(类似于jQuery的选择器啦) 如果jQuery被引入了,则angular.element就可以看作是jQuery选择器,选择的对象可以使用jQuery的函数;如果jQuery不可用,angular.e
- java-给定两个已排序序列,找出共同的元素。
bylijinnan
java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class CommonItemInTwoSortedArray {
/**
* 题目:给定两个已排序序列,找出共同的元素。
* 1.定义两个指针分别指向序列的开始。
* 如果指向的两个元素
- sftp 异常,有遇到的吗?求解
Chen.H
javajcraftauthjschjschexception
com.jcraft.jsch.JSchException: Auth cancel
at com.jcraft.jsch.Session.connect(Session.java:460)
at com.jcraft.jsch.Session.connect(Session.java:154)
at cn.vivame.util.ftp.SftpServerAccess.connec
- [生物智能与人工智能]神经元中的电化学结构代表什么?
comsci
人工智能
我这里做一个大胆的猜想,生物神经网络中的神经元中包含着一些化学和类似电路的结构,这些结构通常用来扮演类似我们在拓扑分析系统中的节点嵌入方程一样,使得我们的神经网络产生智能判断的能力,而这些嵌入到节点中的方程同时也扮演着"经验"的角色....
我们可以尝试一下...在某些神经
- 通过LAC和CID获取经纬度信息
dai_lm
laccid
方法1:
用浏览器打开http://www.minigps.net/cellsearch.html,然后输入lac和cid信息(mcc和mnc可以填0),如果数据正确就可以获得相应的经纬度
方法2:
发送HTTP请求到http://www.open-electronics.org/celltrack/cell.php?hex=0&lac=<lac>&cid=&
- JAVA的困难分析
datamachine
java
前段时间转了一篇SQL的文章(http://datamachine.iteye.com/blog/1971896),文章不复杂,但思想深刻,就顺便思考了一下java的不足,当砖头丢出来,希望引点和田玉。
-----------------------------------------------------------------------------------------
- 小学5年级英语单词背诵第二课
dcj3sjt126com
englishword
money 钱
paper 纸
speak 讲,说
tell 告诉
remember 记得,想起
knock 敲,击,打
question 问题
number 数字,号码
learn 学会,学习
street 街道
carry 搬运,携带
send 发送,邮寄,发射
must 必须
light 灯,光线,轻的
front
- linux下面没有tree命令
dcj3sjt126com
linux
centos p安装
yum -y install tree
mac os安装
brew install tree
首先来看tree的用法
tree 中文解释:tree
功能说明:以树状图列出目录的内容。
语 法:tree [-aACdDfFgilnNpqstux][-I <范本样式>][-P <范本样式
- Map迭代方式,Map迭代,Map循环
蕃薯耀
Map循环Map迭代Map迭代方式
Map迭代方式,Map迭代,Map循环
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年
- Spring Cache注解+Redis
hanqunfeng
spring
Spring3.1 Cache注解
依赖jar包:
<!-- redis -->
<dependency>
<groupId>org.springframework.data</groupId>
<artifactId>spring-data-redis</artifactId>
- Guava中针对集合的 filter和过滤功能
jackyrong
filter
在guava库中,自带了过滤器(filter)的功能,可以用来对collection 进行过滤,先看例子:
@Test
public void whenFilterWithIterables_thenFiltered() {
List<String> names = Lists.newArrayList("John"
- 学习编程那点事
lampcy
编程androidPHPhtml5
一年前的夏天,我还在纠结要不要改行,要不要去学php?能学到真本事吗?改行能成功吗?太多的问题,我终于不顾一切,下定决心,辞去了工作,来到传说中的帝都。老师给的乘车方式还算有效,很顺利的就到了学校,赶巧了,正好学校搬到了新校区。先安顿了下来,过了个轻松的周末,第一次到帝都,逛逛吧!
接下来的周一,是我噩梦的开始,学习内容对我这个零基础的人来说,除了勉强完成老师布置的作业外,我已经没有时间和精力去
- 架构师之流处理---------bytebuffer的mark,limit和flip
nannan408
ByteBuffer
1.前言。
如题,limit其实就是可以读取的字节长度的意思,flip是清空的意思,mark是标记的意思 。
2.例子.
例子代码:
String str = "helloWorld";
ByteBuffer buff = ByteBuffer.wrap(str.getBytes());
Sy
- org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1, column 1
Everyday都不同
$转义el表达式
最近在做Highcharts的过程中,在写js时,出现了以下异常:
严重: Servlet.service() for servlet jsp threw exception
org.apache.el.parser.ParseException: Encountered " ":" ": "" at line 1,
- 用Java实现发送邮件到163
tntxia
java实现
/*
在java版经常看到有人问如何用javamail发送邮件?如何接收邮件?如何访问多个文件夹等。问题零散,而历史的回复早已经淹没在问题的海洋之中。
本人之前所做过一个java项目,其中包含有WebMail功能,当初为用java实现而对javamail摸索了一段时间,总算有点收获。看到论坛中的经常有此方面的问题,因此把我的一些经验帖出来,希望对大家有些帮助。
此篇仅介绍用
- 探索实体类存在的真正意义
java小叶檀
POJO
一. 实体类简述
实体类其实就是俗称的POJO,这种类一般不实现特殊框架下的接口,在程序中仅作为数据容器用来持久化存储数据用的
POJO(Plain Old Java Objects)简单的Java对象
它的一般格式就是
public class A{
private String id;
public Str
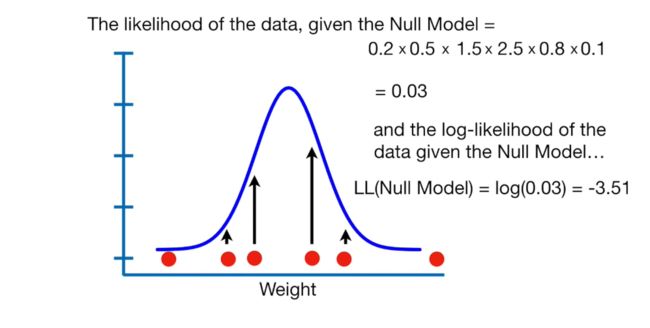
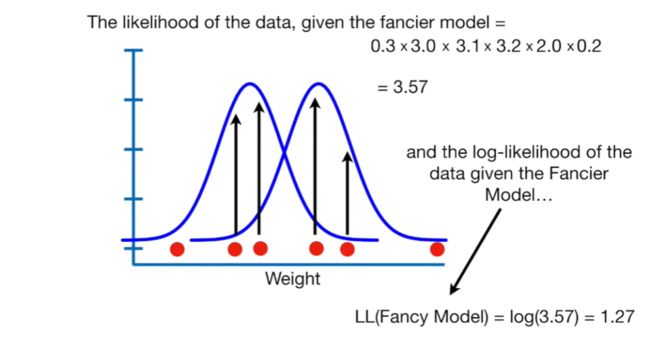
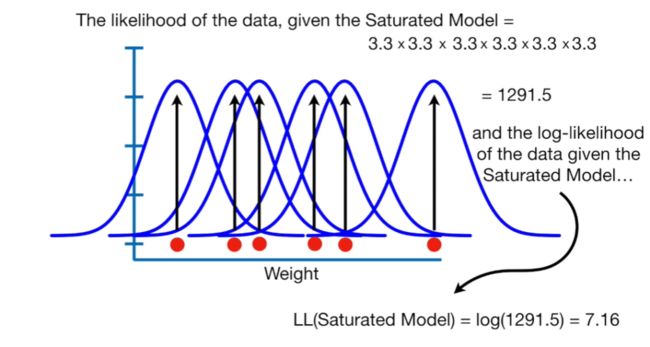

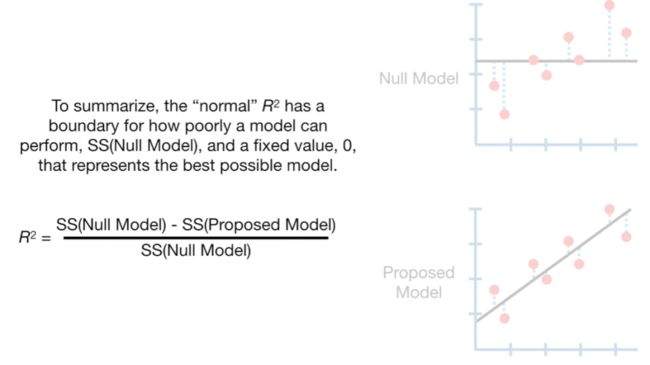
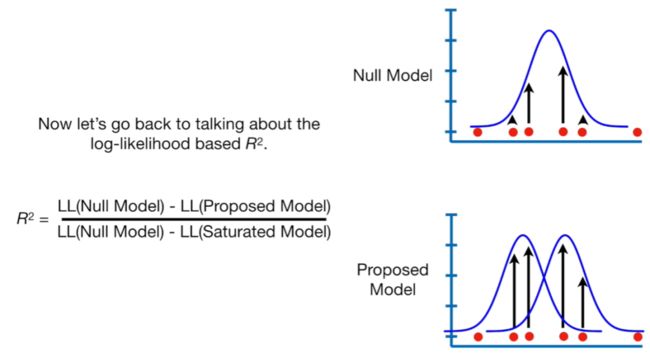
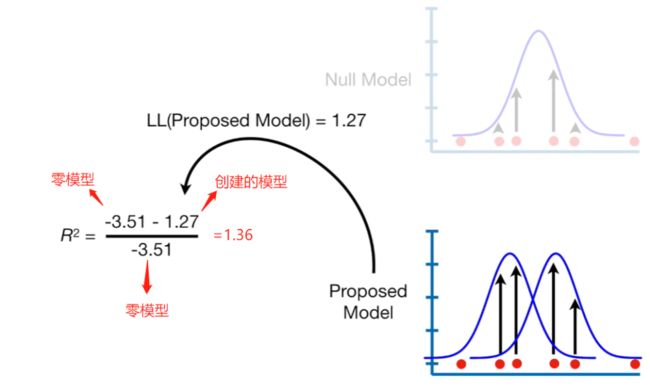
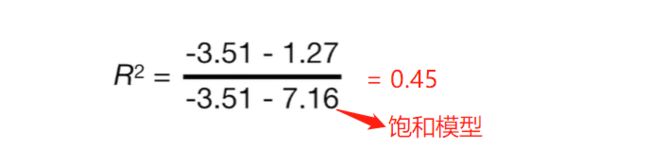
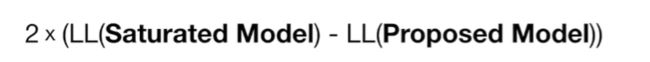


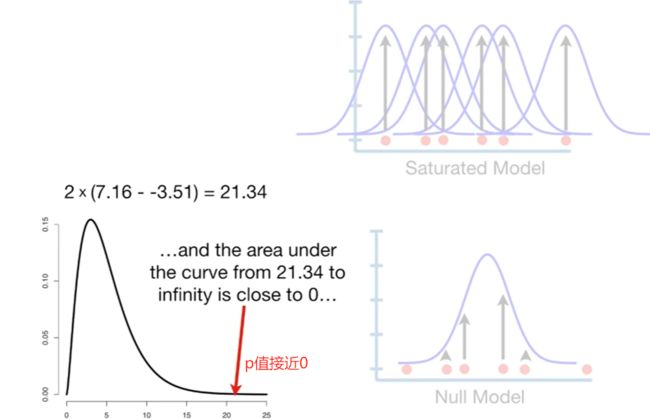
 Null deviance 与residual deviance相减,抵消饱和模型,可以理解为构建模型与零模型的差异。通过该公式,计算出的差值与相同自由度的分布分布相同(自由度为创建模型与零模型的参数数量差异),进而可计算p值。如在本例中,创建模型的参数为2,零模型的参数为1,故对应卡方分布的自由度为1(2-1)。带入公式得出:null deviance - residual deviance = 9.56,对应自由度为1的卡方分布,p值=0.002。
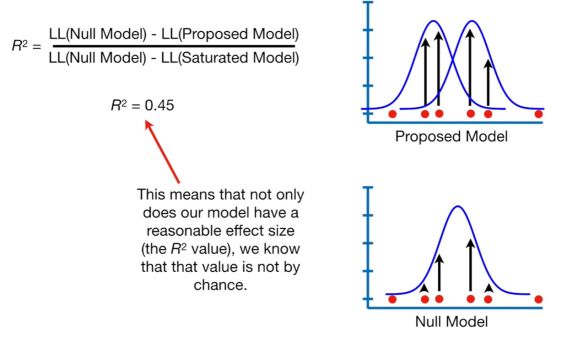
Null deviance 与residual deviance相减,抵消饱和模型,可以理解为构建模型与零模型的差异。通过该公式,计算出的差值与相同自由度的分布分布相同(自由度为创建模型与零模型的参数数量差异),进而可计算p值。如在本例中,创建模型的参数为2,零模型的参数为1,故对应卡方分布的自由度为1(2-1)。带入公式得出:null deviance - residual deviance = 9.56,对应自由度为1的卡方分布,p值=0.002。 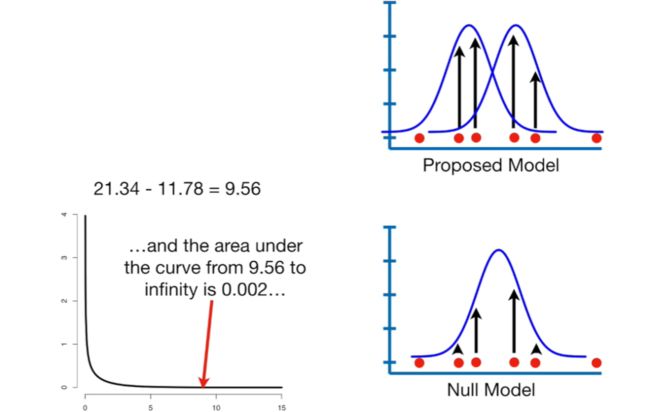
![]()




