支持向量机(SVM)算法之分类实操
python 支持向量机(SVM)算法之分类实操
算法简介
SVM
之前我们用了很多线性算法来做预测模型,像是逻辑算法(LogisticRegression),lasso,岭回归。但现实生活中,很多事情不是线性可分的(即画一条直线就能分类的),而SVM就是专治线性不可分,把分类问题转化为平面分类问题。这个算法中,我们将每一个数据项作为一个点,而在n维空间中(其中n是你拥有的特征数)作为一个点,每一个特征值都是一个特定坐标的值。然后,我们通过查找区分这两个类的超平面来进行分类。
我们用一张图形来说明这一点:
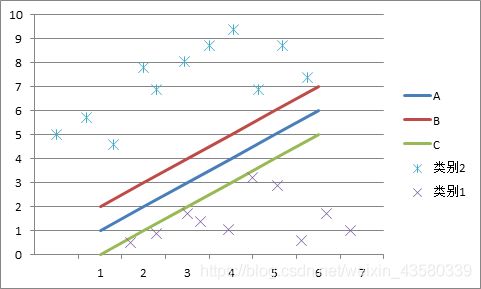
在实际使用过程中,我们并不需要了解确定最佳分类平面的原理,只需要记住一个经验法则来确定正确的超平面:“选择能更好地隔离两个类的超平面”。在这个场景中,蓝色超平面“A”出色地完成了这项工作。
数据来源
胎儿健康分类:https://www.kaggle.com/andrewmvd/fetal-health-classification
![]()
该数据包含胎儿心电图,胎动,子宫收缩等特征值,而我们所需要做的就是通过这些特征值来对胎儿的健康状况(fetal_health)进行分类。
![]()
数据集包含从心电图检查中提取的2126条特征记录,然后由三名产科专家将其分为3类,并用数字来代表:1-普通的,2-疑似病理,3-确定病理。
数据挖掘
1.导入第三方库并读取文件
import pandas as pd
import numpy as np
import winreg
from sklearn.model_selection import train_test_split#划分数据集与测试集
from sklearn import svm#导入算法模块
from sklearn.metrics import accuracy_score#导入评分模块
###################
real_address = winreg.OpenKey(winreg.HKEY_CURRENT_USER,r'Software\Microsoft\Windows\CurrentVersion\Explorer\Shell Folders',)
file_address=winreg.QueryValueEx(real_address, "Desktop")[0]
file_address+='\\'
file_origin=file_address+"\\源数据-分析\\fetal_health.csv"
health=pd.read_csv(file_origin)
#设立桌面绝对路径,读取源数据文件,这样将数据直接下载到桌面上就可以了,省得还要去找
###################
老规矩,上来先依次导入建模需要的各个模块,并读取文件。
2.清洗数据
查找缺失值:
![]()
从上面的结果来看,数据中没有缺失值。
3.建模
train=health.drop(["fetal_health"],axis=1)
X_train,X_test,y_train,y_test=train_test_split(train,health["fetal_health"],random_state=1)
###考虑到接下来可能需要进行其他的操作,所以定了一个随机种子,保证接下来的train和test是同一组数
划分列索引为特征值和预测值,并将数据划分成训练集和测试集。
svm_linear=svm.SVC(C=10,kernel="linear",decision_function_shape="ovr")#参数部分会在下面进行讲解
svm_linear.fit(X_train,y_train)
print("SVM训练模型评分:"+str(accuracy_score(y_train,svm_linear.predict(X_train))))
print("SVM待测模型评分:"+str(accuracy_score(y_test,svm_linear.predict(X_test))))
引入SVM算法,并将算法中的参数依次设立好,进行建模后,对测试集进行精度评分,得到的结果如下:

可以看到,该模型的精度为89%左右。
4.参数
在这里我们只讲解几个重要的参数,对于其它的参数,朋友们可以自行探究。
sklearn.svm.SVC(C,kernel,degree,gamma,coef0,shrinking,probability,tol,cache_size,class_weight,verbose,max_iter,decision_function_shape,random_state)
1.C :惩罚参数,通常默认为1。 C越大,表明越不允许分类出错,但是C越大可能会造成过拟合,泛化效果太低。C越小,正则化越强,分类将不会关注分类是否正确的问题,只要求间隔越大越好,此时分类也没有意义。所以,这其中需要朋友们做一些调整。
2.kernel(核函数) :核函数的引入是为了解决线性不可分的问题,将分类点映射到高维空间中以后,转化为可线性分割的问题。
我们用一张表来说明核函数的几个参数:
(1)Linear核:主要用于线性可分的情形,参数少,速度快,对于一般数据,分类效果已经很理想了。
(2)RBF核:主要用于线性不可分的情形,相比其它线性算法来说这也是一个非常突出的一个优点了。无论是小样本还是大样本,高维还是低维,RBF核函数均适用。
接下来用一段分类边界函数,就能很明显地展现出这两者的区别:
import numpy as np
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight")
np.random.seed(0)
X, y = make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
plt.show()# 手动生成一个随机的平面点分布,并画出来
def plot_decision_boundary(pred_func):
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = 0.01
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
手动设定一个随机的平面分布点
from sklearn import svm
clf = svm.SVC(C=1,kernel="linear",decision_function_shape="ovo")
clf.fit(X, y)
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("SVM-Linearly")
plt.show()
咱们先来瞄一眼线性核分类对于它的分类效果:
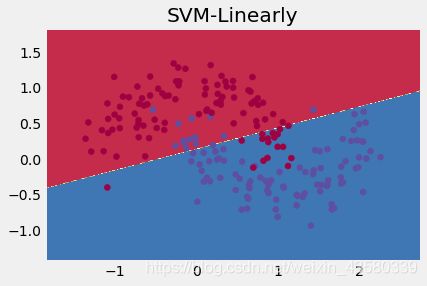
接下来看看rbf核对它进行非线性分类:
clf = svm.SVC(C=1,kernel="rbf",decision_function_shape="ovo")
clf.fit(X, y)
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("SVM-Nonlinearity")
plt.show()
结果如下所示:
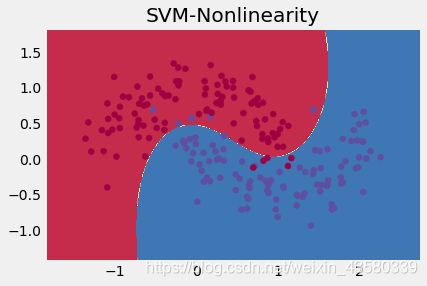
从上面两个图可以很轻松的看出来linear核与rbf核的区别,在上面的两个结果中,很明显rbf核函数的模型精度更好一些。但是在运行过程中,却可以感觉到选用rbf核函数比linear核函数运行速度要稍慢一些,并且随着数据量的增大,运行时间是会一直增加的。
3.decision_function_shape:原始的svm只是用于二分类的问题,如果将其扩展到多分类问题,就要采取一定的融合策略,‘ovo’一对一,就是两两之间进行划分,‘ovr’一对多就是一类与其他类别进行划分。
这里重点讲一下一对多:对每个类别都学习一个二分类模型,将这个类别与其它类别都尽量分开,这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有二分类分类器来进行预测。在对应类别上分数最高的分类器胜出,将这个类别标签返回作为预测结果。
小结
SVM是一种二分类模型,处理的数据可以分为三类:
1.线性可分,通过硬间隔最大化,学习线性分类器,在平面上对应直线
2.近似线性可分,通过软间隔最大化,学习线性分类器
3.线性不可分,通过核函数以及软间隔最大化,学习非线性分类器,在平面上对应曲线
而svm比线性模型要优秀的一个点就是可以处理非线性分类数据,甚至是更高维的数据,例如这样的数据分类:
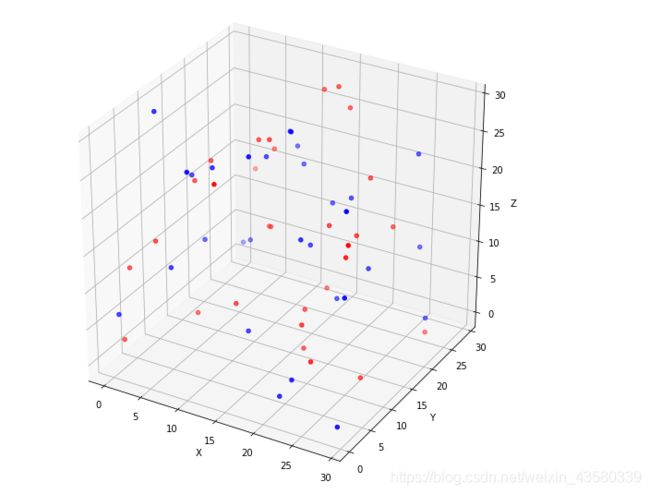
个人博客:https://www.yyb705.com/
欢迎大家来我的个人博客逛一逛,里面不仅有技术文,也有系列书籍的内化笔记。
有很多地方做的不是很好,欢迎网友来提出建议,也希望可以遇到些朋友来一起交流讨论。
