matlab实现fft（快速傅里叶变换），从一维dft开始实现直到实现fft 快速上手写出你的fft

目录

一、基于DFT（自写）FFt（内置）myfft1（自写）比较补零和不补零的区别

二、二维傅里叶变换（快速算法及朴素算法）的实现及各种算法用时比较

三、逆傅里叶变换的算法及代码

正文

一、基于DFT（自写）FFt（内置）myfft1（自写）比较补零和不补零的区别

1、对50个数进行一维傅里叶变换（比较mydft1，myfft1，fft）

代码：

clear
close all
amax = 49;
x = 0:1:amax;
a = 3*x-cos(3.*x);
adft = mydft1(a);%用自写朴素方法进行dft变化
amyfft = myfft1(a);%用自写快速方法进行fft变换
afft = fft(a,amax+1);%用内置快速方法进行fft变换
figure,
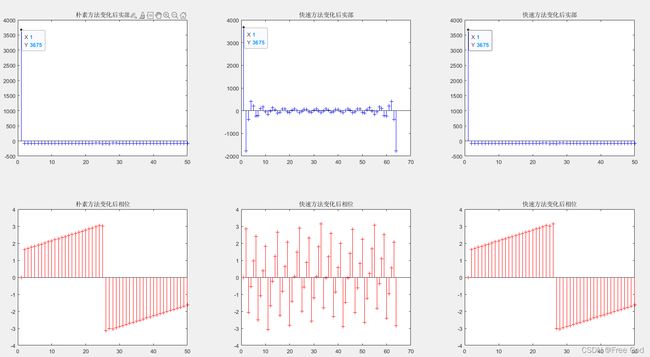
subplot(231),stem(real(adft),'b','+'),title('朴素方法变化后实部')
subplot(234),stem(angle(adft),'r','+'),title('朴素方法变化后相位')
subplot(232),stem(real(amyfft),'b','+'),title('自写快速方法变化后实部')
subplot(235),stem(angle(amyfft),'r','+'),title('自写快速方法变化后相位')
subplot(233),stem(real(afft),'b','+'),title('内置快速方法变化后实部')
subplot(236),stem(angle(afft),'r','+'),title('内置快速方法变化后相位')

图片：

分析：

​ amax = 49，对50个数进行离散度立叶变换，观察到mydft1（自写朴素方法）输出图像与fft（50）（内置快速方法）输出图像相同，但是与myfft1（自写快速方法）输出图像不相等，并非我所写函数错误，而是频域采样间隔不同，我利用快速傅里叶算法计算，对输入数列长度不等于2^n（n为正整数）的数列进行了补零，缩短了频域的采样间隔，使该其曲线更光滑，补零后长度改变，所以具体数值发生改变，但是三幅图像的零频都是相同的（零频等于该一维数列遍历求和）。

2、对64个数进行一维傅里叶变化（比较mydft1，myfft1，fft）

代码：

clear
close all
amax = 63;
x = 0:1:amax;
a = 3*x-cos(3.*x);
adft = mydft1(a);%用自写朴素方法进行dft变化
amyfft = myfft1(a);%用自写快速方法进行fft变换
afft = fft(a,amax+1);%用内置快速方法进行fft变换
figure,
subplot(231),stem(real(adft),'b','+'),title('朴素方法变化后实部')
subplot(234),stem(angle(adft),'r','+'),title('朴素方法变化后相位')
subplot(232),stem(real(amyfft),'b','+'),title('自写快速方法变化后实部')
subplot(235),stem(angle(amyfft),'r','+'),title('自写快速方法变化后相位')
subplot(233),stem(real(afft),'b','+'),title('内置快速方法变化后实部')
subplot(236),stem(angle(afft),'r','+'),title('内置快速方法变化后相位')

图片：

分析：

​ amax = 63，是对64（=2^6）个数进行离散傅里叶变换，观察到三个图像均相同，是因为我对fft（64）（内置快速方法）输入的是64个数，三个图像的频域采样间隔相同，即输出相同图像。

3、一维数列补零前后变化（数列长度分别为：64，256，512）

代码：

clear
close all
amax = 49;
x = 0:1:amax;
a = 3*x-cos(3.*x);
a1 = myfft1(a,2^6);a1L = length(a1);
a2 = myfft1(a,2^8);a2L = length(a2);
a3 = myfft1(a,2^9);a3L = length(a3);
figure,
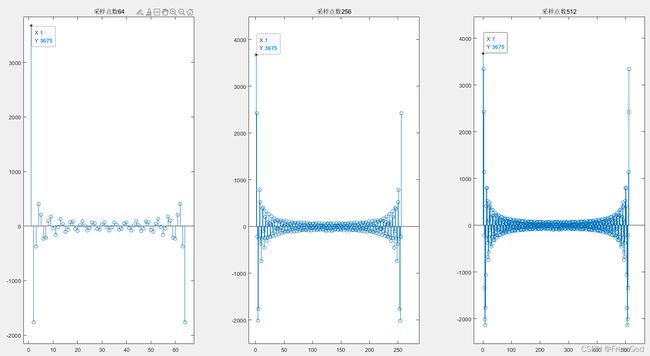
subplot(131),stem(real(a1)),title("采样点数"+a1L);
subplot(132),stem(real(a2)),title("采样点数"+a2L);
subplot(133),stem(real(a3)),title("采样点数"+a3L);

图片：

分析：

​ 零频相同，大致轮廓相同，补零越多，频域采样间隔越短，曲线越光滑。

​ 补零还应用于消除由栅栏效应引起的频谱泄露。

4、自写函数代码（mydft1，myfft1）

一维dft代码

function [fy,sumY] = mydft1(y,dx,xLeft,xRight)
%一维离散傅里叶变换
%该函数是用于输入一个 函数 或 列向量 即y ，将y傅里叶变换后输出
%fy是y的离散傅里叶变换，sumY是fy的零频，即y的各个数相加
%此函数输出y傅里叶变换后的1、实部2、幅值3、相位
% 创建命名函数的函数句柄：
% fy = @myfun
% 创建匿名函数的函数句柄：
% fxy = @(x,y) x.^2 + y.^2;
if length(y) ==1
    x = xLeft:dx:xRight;
    y = y(x);
    fy = y;
else
    x = 0:1:length(y)-1;
end  
for x1 = 0:length(y)-1
   temp = 0;
   for x2 = 0:length(y)-1
       temp = temp + y(x2+1)*exp(-1j*2*pi*x1*x2/length(y));
   end
   fy(x1+1) = temp;
end
sumY = sum(y(:));
end

一维fft

function fOut = myfft1(a,M)
%a是输入的一串一维向量，M是2^n大小的数值，M可以不输入，则默认补充最邻进的那个2^n整数值
%快速傅里叶变换（碟式变换作为原理）
aL = length(a);
if nargin<2
    n = 1;
    while(aL > 2^n)
        n  = n+1;
    end
    aADD = zeros(1,2^n);
else
    aADD = zeros(1,M);
    n = log2(M);
end
aADD(1:aL) = a;
aL1 = length(aADD);
%对位置进行二进制取反后转为10进制
x = bin2dec(fliplr(dec2bin(0:aL1-1,n)))+1;
a1 = aADD(x);

%碟式变换的级数
for f1 = 1:n
    %碟式变换中，数值的间隔
    space = 2^(f1-1);
    for f2 = 0:space-1
        %奇数项的旋转因子
        factor = 2^(n-f1)*f2;
        for f3 = f2+1:2^f1:aL1
            %复数项
            W = exp(-1j*2*pi*factor/aL1);
            %先存一下a1（k）
            temp = a1(f3)+a1(f3+space)*W;
            %重复对a1调用即可，无需新的变量
            a1(f3+space) = a1(f3)-a1(f3+space)*W;
            a1(f3) = temp;
        end
    end
end
fOut = a1;
end

二、二维傅里叶变换（快速算法及朴素算法）的实现及各种算法用时比较

1、对三幅图像进行快速傅里叶变化

代码：

close all
clear
aIn1 = imread('ganshe.jpg');
aIn2 = imread('ganshe1.jpg');
aIn3 = imread('fly.jpg');
%在函数内部已用.*(-1).^(X+Y)移频处理
[a1Abs1,a1Log1] = myfft2(aIn1);
[a1Abs2,a1Log2] = myfft2(aIn2);
[a1Abs3,a1Log3] = myfft2(aIn3);

图片：

2、比较mydft2（自写朴素算法），myfft2（自写快速算法），fft2（内置快速算法）所用时间

代码：

clear
close all
aIn = imread('fly.jpg');
%朴素dft处理二维图像所用时间
tic
[aAbs2,aLog2] = mydft2(aIn);
toc
disp(['二维离散傅里叶变换朴素方法运行时间：',num2str(toc)]);

%自写fft处理二维图像所用时间
tic
[aAbs,aLog] = myfft2(aIn);
toc
disp(['二维离散傅里叶变换自写快速方法运行时间: ',num2str(toc)]);

%内置fft处理二维图像所用时间
tic
aAbs1 = fftshift(abs(fft2(aIn)));
aLog1 = log(aAbs1+1);
toc
disp(['二维离散傅里叶变换内置快速方法运行时间: ',num2str(toc)]);

图片：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-snBpBCW7-1641879908403)(E:\Homework\数字图像处理\课上\图片\78.png)]

分析：

图像原始大小为1026*1026；

mydft2 处理的图像大小为：1026*1026；耗时508 秒*（约为8分27秒）

myfft2 处理的图像大小为：2048*2048；耗时23.6 秒（约为0.39分）

fft2 处理的图像大小为：2048*2048；耗时0.161 秒（约为0.0026分）

3、myfft1对数组变换后并非严格等于fft，讨论过程如下

代码：

close all
clear
%用fft和myfft1对a1进行傅里叶变换，结果相减
a1 = (1:10);
a11 = myfft1(a1);
a22 = fft(a1,16);
delta = a22-a11;
subplot(121),plot(0:1:15,real(delta)),title('实部相差');
subplot(122),plot(0:1:15,imag(delta)),title('虚部相差');

图片：

分析：

可见相减后不等于0，但是其量级十分微小（$10^{-15} $）量级，可以忽略。

4、自写函数代码（mydft2，myfft2）

二维dft

function [afft2Abs,afft2Log]=mydft2(aIn)
%不建议采用这个函数作为大图像的傅里叶变换，建议使用myfft2
%输入aIn图像（无大小限制），输出移频后的幅值和经过log（aIn+1）处理的值
aDouble = im2double(aIn);
[ra,ca] = size(aDouble);
[X,Y] = meshgrid(0:ra-1,0:ca-1);
afft2 = aDouble.*(-1).^(X+Y);
for f1 = 1:ra
    aLine = afft2(f1,:);
    afft2(f1,:) = mydft1(aLine);
end
for f2 = 1:ca
    aCol = afft2(:,f2);
    afft2(:,f2) = mydft1(aCol);
end
afft2Abs = abs(afft2);
afft2Log = log(afft2Abs+1);
figure,
subplot(131),imshow(aIn,[]),title('原图');
subplot(132),imshow(afft2Abs,[]),title('频谱(移频后)图');
subplot(133),imshow(afft2Log,[]),title('log（灰度值+1）处理图');
end

二维fft

function [afft2Abs,afft2Log] = myfft2(aIn)
%快速二维傅里叶变换
%aIn是输入图像，不管输入什么形状，最终会变为边长为2^n的正方形
%afft2Abs是对aIn进行二维傅里叶变换的移频后的结果
%afft2Log是对afft2Abs进行log（afft2Abs+1）处理的结果（增强了细节）
aDouble = im2double(aIn);
[ra,ca] = size(aDouble);
maxL = max(ra,ca);
n = 1;
while(maxL>2^n)
   n = n+1;
end
aZeros = zeros(2^n,2^n);
aZeros(1:ra,1:ca) = aDouble;
afft2 = aZeros;
[Ra,Ca] = size(afft2);
[X,Y] = meshgrid(0:Ra-1,0:Ca-1);
afft2 = afft2.*(-1).^(X+Y);
for f1 = 1:Ra
    aLine = afft2(f1,:);
    afft2(f1,:) = myfft1(aLine);
end
for f2 = 1:Ca
    aCol = afft2(:,f2);
    afft2(:,f2) = myfft1(aCol);
end
afft2Abs = abs(afft2);
afft2Log = log(afft2Abs+1);
figure,
subplot(131),imshow(aIn,[]),title('原图');
subplot(132),imshow(afft2Abs,[]),title('频谱(移频后)图');
subplot(133),imshow(afft2Log,[]),title('log（灰度值+1）处理图');
end

三、逆傅里叶变换的算法及代码

1、原理

简述：将频域里的$F\left( u,v \right) $取复共轭得$F^\left( u,v \right) $，将$F^\left( u,v \right) $带入正变换中，得到$MNf^\left( x,y \right) $，将$MNf^\left( x,y \right) $除以$MN$后取复共轭（实数的复共轭就是实数），即得到傅里叶逆变换结果$f\left( x,y \right) $。

2、代码

myifft1代码

function [aOut,aNum] = myifft1(aIn,aL)
%这仅仅是一维 傅里叶 逆变换
%输入必须为2^n格式，输出也是2^n格式,aL调整输出的数量
aInCon = conj(aIn);
[afx,afxL] = myfft1(aInCon);
aifx = afx/afxL;
if nargin<2
    aOut = real(aifx);
    aNum = length(aOut);
else
    aOut = real(aifx(1:aL));
    aNum = aL;
end

myifft2代码

function [aOut,Ra,Ca] = myifft2(aIn,x,y)
aCon = conj(aIn);
afft2 = myfft2(aCon);
[ra,ca] = size(afft2);
aifft2 = afft2/(ra*ca);
aifft2(abs(aifft2)<10^-8) = 0;
aifft2 = real(aifft2);
if nargin == 3
    aifft2 = aifft2(1:x,1:y);
end
aOut = aifft2;
[Ra,Ca] = size(aOut);
end