Decoupled Networks 论文笔记

0 摘要

    基于内积运算的卷积操作一直是卷积神经网络（CNN）的核心组件，也是学习视觉表示的关键。我们观察发现，CNN学习的特征是类内差异（特征的幅值）和类间差异（特征间的夹角，语义差异）的耦合。我们提出了一种通用的解耦学习框架，该框架对类内差异和类间差异进行独立的建模。具体而言，我们首先将内积重新分解为解耦的形式，然后将其推广到解耦卷积算子，利用该算子构建解耦网络。我们提出了解耦卷积算子的几个实例。每个解耦算子具有直观的几何解释。基于这些解耦算子，解耦网络直接从数据中学习。大量实验表明，这种解耦具有比较显着的性能，并且易于收敛，鲁棒性更强。

1 介绍

    卷积神经网络推动了许多视觉任务的发展，包括物体识别，物体检测，语义分割等。最近的研究中有相当一部分对CNN的结构进行改进（如ResNet的short cut和GoogLeNet的多分支卷积），他们着重于提高网络深度和表示能力。 尽管取得了这些进展，但理解卷积网络是如何产生有区分力的表示，并且能良好地泛化仍然是一个有趣的问题。
    目前的卷积操作： f(w,x)=<w,x>=wTx f ( w , x ) =< w , x >= w T x ，其本质上是一个矩阵相乘计算两个矩阵的相似度操作。这个操作将类间差异和类内差异统一在一个度量中。因此，当两个样本之间的内积较大时，无法判断这两个样本是类内差异造成的还是类间的差异造成的。（也就是说当你通过卷积操作得到的结果很相似的时候，你并不能够得到一个结论说这两个很相似，反之亦不能，因为你不能够区别这种差异或者是相似度是类内差异造成的还是类间的差异造成的）。为了更好地研究CNN表示的属性并进一步改进现有框架，我们建议明确区分类间差异和类内变异。具体来说，我们用幅值和角度来重新设计内积，比如： ||w||2||x||2cos(θ(w,x)) | | w | | 2 | | x | | 2 c o s ( θ ( w , x ) ) 。

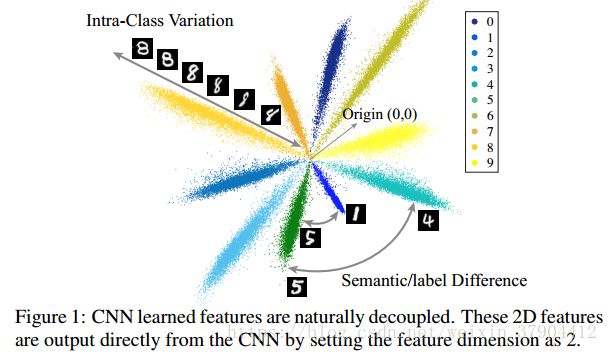
图1是CNN在手写体识别任务上学到的特征的2D可视化示意图。 0~9每一个手写体数字对应的特征是图中的一束；任意一束当中的不同位置表示的是同一类别的不同表征，也就是类间差距（intra-class Variations）；束与束之间形成的夹角表达的是两个类别之间的差距（inter-class difference），也就是这里所谓的语义差异。这种解耦现象促使我们提出解耦卷积算子。我们希望内积中的解耦幅值和角度能更好地模拟深层网络中的类内差异和类间差异。
    我们通过将传统的基于内积的卷积算子推广到解耦算子，提出了一种新的解耦网络（DCNet）。（如果不解耦会存在一个什么样的问题呢？就是说你只能得到一个最终的结果，但是对于两个同样的输出，你不能分辨造成这个结果的原因是因为他们实际就是同一种类别，还是因为刚好 ab =cd。）那么具体怎么解耦呢？ 作者给出的解决方案：
f(w,x)=||w||2||x||2cos(θ(w,x))=h(||w||,||x||)×g(θ(w,x)) f ( w , x ) = | | w | | 2 | | x | | 2 c o s ( θ ( w , x ) ) = h ( | | w | | , | | x | | ) × g ( θ ( w , x ) ) 。
其中， θ=arccoswTx||wT||2||x||2 θ = a r c c o s w T x | | w T | | 2 | | x | | 2
    将卷积操作解耦为幅值（Norm）和角度（Angle）两部分，并且将这两部分分别用两个函数 h(.) h ( . ) 和 g(.) g ( . ) 来表示。关于角度的函数 g(.) g ( . ) 则度量着类间差异（inter-class difference），关于幅值的函数 h(.) h ( . ) 则度量着类内差异（intra-class variations），同时其值的大小也就表示了这个类别的可信度。解耦卷积提供了一种更通用的框架以更好区分类间差异和类内差异，并且传统的卷积操作就变成了解耦网络的一个特例： h(||w||,||x||)=||w||2||x||2,g(θ(w,x))=cos(θ(w,x)) h ( | | w | | , | | x | | ) = | | w | | 2 | | x | | 2 , g ( θ ( w , x ) ) = c o s ( θ ( w , x ) ) 。
    从解耦的角度来看，原始的CNN基于一个强有力的假设，即类内变异可以通过范式乘法来线性建模，而类间差异由角度余弦来描述。 但是，这种建模方法不一定适用于所有任务。 通过解耦学习框架，我们可以根据不同的任务设计解耦运算符，也可以直接从数据中学习。 DCNets的优点有四个方面：
1.DCNets不仅允许我们使用一些替代函数来更好地模拟类内差异和类间差异，而且它们还使我们能够直接学习这些函数，而不是拟合它们。
2.DCNets可以更快地收敛，同时达到与原始CNN相当甚至更好的精度。
3.DCNets的一些实例可以具有更强的鲁棒性可以抵抗对抗样本的攻击。我们可以用有界的 h(⋅) h ( · ) 来压缩每个类的特征空间，这可以带来鲁棒性。
4.解耦的运算符非常灵活，并且与架构无关。 他们可以很容易地适应VGG，GoogLeNet，ResNet。
    具体而言，我们提出了两种不同类型的解耦卷积算子：有界算子和无界算子。 我们为每种类型的解耦算子提供多个实例。 从经验上讲，有界算子可能会产生更快的收敛速度和更好的抵抗对抗样本攻击的鲁棒性，无界算子可能具有更好的表征能力。 这些解耦算子可以是平滑的也可以是不平滑的，会产生不同的行为。 此外，我们引入了一个新的概念： 解耦算子的算子半径operator radius。算子半径描述了幅值函数 h(⋅) h ( · ) 的导数相对于输入 ||x|| | | x | | 的变化。 通过反向传播学习算子半径，我们进一步提出了可学习的解耦算子。 此外，我们还展示了一些优化这些算子的替代方法，这些算子由标准的反向传播学习。。我们的贡献如下：
1.受CNN特征解耦观察的启发，我们提出了一个解耦框架来研究神经网络。
2.传统CNNs对类间差异和类内差异做了强有力的假设，这可能不是最优的。 通过解耦内积，我们能够设计更有效的幅度和角度函数。
3.与标准CNN相比，DCNets更容易收敛，精度更高，鲁棒性更强。

2 相关工作

    越来越多的工作侧重于改善分类层（最后一个softmax层）以增加学习特征的区分性。 相反，解耦学习提供了一个更加普遍和更加系统的方式来研究CNN。在我们的框架中，先前的工作（改善分类层）可以看成对最后的softmax层优化 h(||w||,||x||) h ( | | w | | , | | x | | ) 和 g(θ(w,x)) g ( θ ( w , x ) ) 。例如，权重归一化等效于 h(||w||,||x||)=||x|| h ( | | w | | , | | x | | ) = | | x | | ，输入归一化等效于 h(||w||,||x||)=||w|| h ( | | w | | , | | x | | ) = | | w | | 。

3 解耦网络

3.1 解耦重构卷积

传统的卷积网络中的卷积运算是计算输入 x x 与权重w w 的内积（ w w 和x x 都是列向量）：
f(w,x)=<w,x>=wTx(1) f ( w , x ) =< w , x >= w T x ( 1 )
这种形式可以进一步解耦写成幅值和夹角分离的形式：
f(w,x)=||w||2||x||2cos(θ(w,x))(2) f ( w , x ) = | | w | | 2 | | x | | 2 c o s ( θ ( w , x ) ) ( 2 )
其中 θ(w,x) θ ( w , x ) 是输入 x x 与权重w w 之间的夹角。我们提出的解耦卷积运算的通用形式是：
f(w,x)=h(||w||,||x||)×g(θ(w,x))(3) f ( w , x ) = h ( | | w | | , | | x | | ) × g ( θ ( w , x ) ) ( 3 )
明确分离了输入 x x 与权重w w 的范数和它们之间的夹角，我们定义 h(||w||,||x||) h ( | | w | | , | | x | | ) 为幅值函数， g(θ(w,x)) g ( θ ( w , x ) ) 为角度函数。很容易看出，传统卷积运算是解耦卷积运算的一种特例。从公式中可以看到，我们是基于类间差异和类内差异进行的解耦。

3.2 解耦卷积算子

    我们讨论如何更好地模拟类内差异，然后给出一些解耦算子的实例。

3.2.1 模拟类内差异

    函数 g(⋅) g ( · ) 的设计相对容易，因为它只将角度作为输入。相反，函数 h(⋅) h ( · ) 将 w w 的范数和x x 的范数作为输入，因此设计更复杂。我们这里讨论的都是不加权的解耦操作子，也就是说所有的权重被认为是同等的重要： h(||w||,||x||)=h(||x||) h ( | | w | | , | | x | | ) = h ( | | x | | ) 。这样的操作简化了操作同时也保证了准度。将 w w 与h(⋅) h ( · ) 相结合，解耦运算符成为加权解耦算子。将 w w 并入h(⋅) h ( · ) 有多种方法，稍后我们将讨论并地评估这些变体。

3.2.2 有界解耦算子

    有界运算符的输出必须是常量，与输入和卷积核权重无关，即，解耦算子 |fd(w,x)|≤c | f d ( w , x ) | ≤ c ，其中c是正常数。 为简单起见，我们首先考虑不加权的解耦操作子（即 w w 不包含在h(⋅) h ( · ) 中）。
超球面卷积（SphereConv）:即， h(||w||,||x||)=α h ( | | w | | , | | x | | ) = α 。解耦算子公式如下：
SphereConv:fd(w,x)=α×g(θ(w,x))(4) S p h e r e C o n v : f d ( w , x ) = α × g ( θ ( w , x ) ) ( 4 )
其中, α>0 α > 0 控制输出尺度。 g(θ(w,x)) g ( θ ( w , x ) ) 取决于单位超球面上的测地距离（测地距离的意思就是在三维空间中，两点之间的最短路径，归根究底就是最短路径，在三维中间从一个点到另外一个点的路径有无数种，但是最短路径只有一条，那么这个最短路径的长度就是测地距离 geodesic distance），并且通常输出值的范围在 [−1,1] [ − 1 , 1 ] ，所以最终算子输出在 [−α;α] [ − α ; α ] 。 通常，我们可以令 α=1 α = 1 。 在几何上，SphereConv可以被看作是投射 w w 和x x 到超球面上，然后执行内积运算（如果 g(θ)=cos(θ) g ( θ ) = c o s ( θ ) ）。
     简单总结：对于任何一个类别，其实我并不关心他们的类内差异，我只想要得到一个最终的类间差异，因此，我将这个最终决定权全部交给 g(⋅) g ( · ) 。所以你会发现所有的类别的特征都会投影在一个球面（Sphere）上面。
超球卷积（BallConv）：即， h(||w||,||x||)=αmin((||x||,ρ)ρ) h ( | | w | | , | | x | | ) = α m i n ( ( | | x | | , ρ ) ρ ) 。解耦算子公式如下：
BallConv:fd(w,x)=α×min((||x||,ρ)ρ)×g(θ(w,x))(5) B a l l C o n v : f d ( w , x ) = α × m i n ( ( | | x | | , ρ ) ρ ) × g ( θ ( w , x ) ) ( 5 )
其中, ρ ρ 控制输入范数 ||x|| | | x | | 的饱和阈值（球的半径）， α>0 α > 0 控制输出尺度。当 ||x||>ρ | | x | | > ρ ， h(.) h ( . ) 饱和，并且 h(.)=α h ( . ) = α ；当 ||x||<ρ | | x | | < ρ ， h(.) h ( . ) 随着 ||x|| | | x | | 线性增长。在几何学上，BallConv可以看作是将 w w 投影到超球面上，将x x 投影到超球体，然后执行内积运算（如果 g(θ)=cos(θ) g ( θ ) = c o s ( θ ) ）。BallConv比SphereConv更加健壮和灵活，就收敛性而言，BallConv仍然可以帮助网络收敛，因为它的输出范围与SphereConv的范围相同。
     简单总结：从名字来讲我们就知道，特征的投影会是一个实心的球（Ball），也就是说我考虑类内的差异，但是这个差异有一个上界那就是这个球的球面，而在球的内部，其重要性是和输入相关的。
双曲正切卷积（TanhConv）：我们提出了一个光滑解耦算子，称为双曲正切卷积（TanhConv）。 TanhConv使用双曲正切函数来替换BallConv中的阶跃函数，可以将其表述为：
TanhConv:fd(w,x)=α×tanh(||x||ρ)×g(θ(w,x))(6) T a n h C o n v : f d ( w , x ) = α × t a n h ( | | x | | ρ ) × g ( θ ( w , x ) ) ( 6 )
其中, tanh(⋅) t a n h ( · ) 表示双曲正切函数， ρ ρ 是控制衰减曲线的参数。 TanhConv可以看作是BallConv的一个平滑版本，它不仅与BallConv有着相同的优势，而且由于其平滑性而具有更多的收敛增益。
总结：SphereCov更多是投影在球面的，而后面的两个理论上可以看做是一个实心的。

3.2.3 无界解耦算子

线性卷积：最简单的无界解耦算子是线性卷积：
LinearConv:fd(w,x)=α×||x||×g(θ(w,x))(7) L i n e a r C o n v : f d ( w , x ) = α × | | x | | × g ( θ ( w , x ) ) ( 7 )
其中, α>0 α > 0 控制输出尺度。LinearConv不同于原始卷积，因为它将权重投影到超球面并具有一个控制范围的参数。
分段卷积（SegConv）：

SegConv:fd(w,x)={α×||x||×g(θ(w,x))(β||x||+αρ−βρ)×g(θ(w,x))0≤||x||≤ρρ<||x||(8) S e g C o n v : f d ( w , x ) = { α × | | x | | × g ( θ ( w , x ) ) 0 ≤ | | x | | ≤ ρ ( β | | x | | + α ρ − β ρ ) × g ( θ ( w , x ) ) ρ < | | x | | ( 8 )

LinearConv和BallConv都是SegConv的特例。
对数卷积（LogConv）：另一种平滑的解耦算子。
LogConv:fd(w,x)=α×log(1+||x||)×g(θ(w,x))(9) L o g C o n v : f d ( w , x ) = α × l o g ( 1 + | | x | | ) × g ( θ ( w , x ) ) ( 9 )
混合卷积（MixConv）：结合了多个解耦卷积算子并享有更好的灵活性。 由于混合卷积有许多可能的组合，因此我们只考虑LinearConv和LogConv的加法组合：
MixConv:fd(w,x)=(α×||x||+β×log(1+||x||)×g(θ(w,x))(10) M i x C o n v : f d ( w , x ) = ( α × | | x | | + β × l o g ( 1 + | | x | | ) × g ( θ ( w , x ) ) ( 10 )

3.2.4 解耦算子的属性

算子半径：算子半径被定义为描述幅度函数 h(.) h ( . ) 的梯度变化点。 算子半径将划分幅度函数划分为两个阶段。在这两个阶段，幅度函数通常具有不同的梯度范围，因此在优化期间的表现不同。 我们令 ρ ρ 为每个解耦算子的算子半径：
BallConv，当 ||x||<ρ | | x | | < ρ 时，幅度函数将被激活，并且它将随 ||x|| | | x | | 线性增长；当 ||x||>ρ | | x | | > ρ 时，幅度函数将失效并输出一个常数。
SegConv， ||x||=ρ | | x | | = ρ 是幅度函数斜率的变化点。
SphereConv，LinearConv，LogConv的算子半径被定义为零，表示它们没有算子半径。

边界：解耦算子的有界性可能会影响其收敛速度和鲁棒性。 [使用有界算子可以提高收敛性，原因有两个。 首先，有界算子通过随机梯度下降训练深度网络可以更好地调节问题。 其次，有界运算符使输出的方差很小，并部分解决内部协变量移位问题。有界算子也可以使整个网络更加平滑。相反，无界算子可能比有界算子具有更强的逼近能力和灵活性。

平滑度： 幅度函数的平滑性会直接影响网络的拟合能力和收敛性。 一般来说，使用平滑幅度函数可以更好的拟合，也能更稳定和更快的收敛。 然而，因为用多项式逼近平滑函数可能更困难，平滑的幅度函数在计算上更昂贵。

3.3 几何解释

    所有解耦卷积算子都有明确的几何解释，如图2。因为所有解耦算子都对权重进行归一化，所以所有权重都已经被投影在单位超球面上。

SphereConv还将输入向量 x x 投影到单位超球面上，然后根据超球面上的测地距离（乘以比例因子α α ）计算 w w 和x x 之间的相似度。 因此，其输出范围在 [−α,α] [ − α , α ] ，并且仅取决于 w w 与x x 的方向（假设 g(θ(w,x) g ( θ ( w , x ) 在 [−1;1] [ − 1 ; 1 ] 的范围内）。
BallConv首先将输入向量 x x 投影到超球体上，然后根据超球体内的投影x x 和超球面上的标准化 w w 计算相似度。 具体而言，如果||x||>ρ | | x | | > ρ ，BallConv将 x x 投射到超球体。 TanhConv是一个平滑的BallConv，具有相似的几何解释。
SegConv比SphereConv和BallConv更灵活。 LinearConv是最简单的无界算子，它的幅度函数随||x|| | | x | | 线性增长。LogConv使用对数函数来转换输入 x x 的标准。

3.4 角度函数的设计

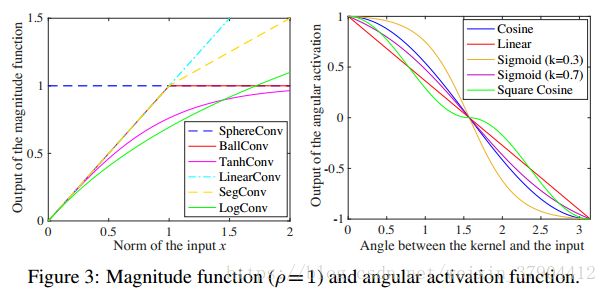
    g(.) g ( . ) 是一个关于 θ θ 的函数，大多数实际上是一个非线性的函数，也就是说其实就是一个激活函数，所以称之为角度激活函数（Angular activation）。 那么理论上来讲，这样的操作子是不需要再有一个激活函数的。这里列出了几种 g(.) g ( . ) 的选择：
Linear:g(θ(w,x))=−2πθ(w,x)+1 L i n e a r : g ( θ ( w , x ) ) = − 2 π θ ( w , x ) + 1 ，它的输出随着 θ(w,x) θ ( w , x ) 线性增长。
Cosine:g(θ(w,x))=cos(θ(w,x)) C o s i n e : g ( θ ( w , x ) ) = c o s ( θ ( w , x ) ) ，它被用于原始卷积算子中。
Sigmoid:g(θ(w,x))=1+exp(−π2k)1−exp(−π2k)×1−exp(θ(w,x)k−π2k)1+exp(θ(w,x)k−π2k) S i g m o i d : g ( θ ( w , x ) ) = 1 + e x p ( − π 2 k ) 1 − e x p ( − π 2 k ) × 1 − e x p ( θ ( w , x ) k − π 2 k ) 1 + e x p ( θ ( w , x ) k − π 2 k )
Squareconsine:g(θ(w,x))=sign(cos(θ))×cos2(θ) S q u a r e c o n s i n e : g ( θ ( w , x ) ) = s i g n ( c o s ( θ ) ) × c o s 2 ( θ )

3.5 加权解耦算子

    我们发现不考虑加权的解耦算子在大多数情况下比加权算子效果更好。略

4 实验

实验的部分，作者做了大量的实验，不仅比较了设计的DN网络的收敛性，非线性，BN功能，而且还和ResNet等比较下目标识别任务上的准确度，此外作者还对网络对于对抗样本攻击的性能进行了比较。在所有的比较当中作者都得到了最好的结果。主要看以下几个方面的比较：
1.在CIFAR100上和没有BN的CNN

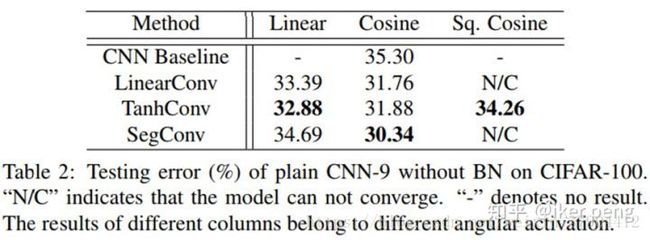
注意，这个表格当中，每一行都是一个 卷积操作子也就是 h(.) h ( . ) 函数，每一列都是一个角度激活函数 g(.) g ( . ) 。因此，如之前所说，对于一个一般CNN 就是 g(.)=cos g ( . ) = c o s 。
结果显示，即便是没有BN，DN都能够表现出绝对的优势。
2.操作子的非线性的比较

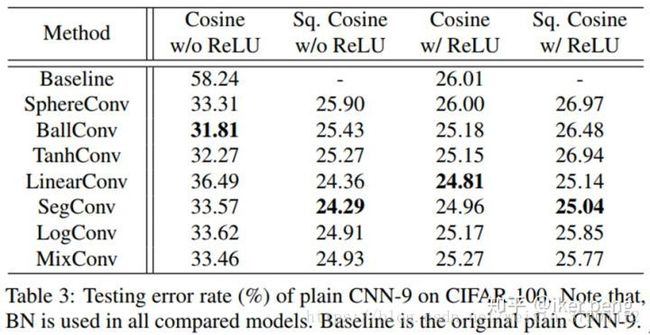
第一列的比较非常明显的看出，在没有ReLU激活函数的情况下，一般的CNN可以达到高达58%以上的错误率，而对于DN来讲只有差不多30%；而从第三列再加上ReLU之后，DN的性能也好于传统的CNN。
3.目标识别性能比较

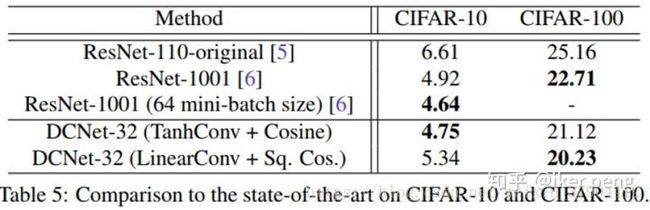
作者是 CIFAR10 和CIFAR100 两个数据集上面和当前最好的网络模型进行了分类准确度的比较，我们可以看出。DN都可以拿到最好的结果。同时作者也在ImageNet-2012上进行了比较，也同样拿到了最好的效果：

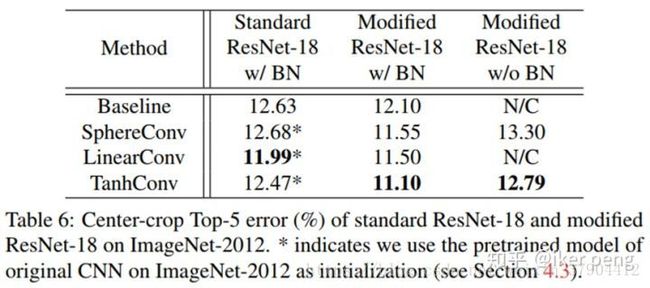
4.对抗样本攻击的比较

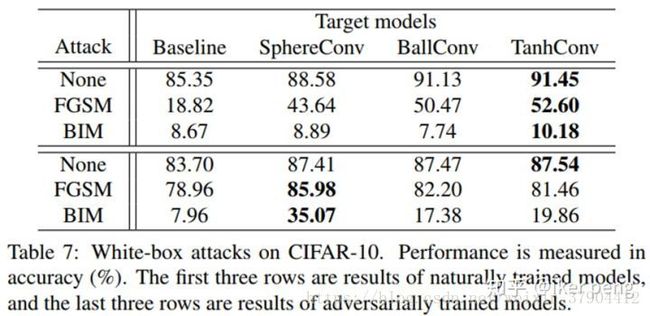
作者在黑盒和白盒的情况下，比较了两种算法的攻击：FGSM和BIM。结果显示其具有更好的防止攻击的能力。