python 笔记:爱因斯坦求和 einsum
1 einsum简介
使用爱因斯坦求和约定,可以以简单的方式表示许多常见的多维线性代数数组运算。
给定两个矩阵A和B,我们想对它们做一些操作,比如 multiply、sum或者transpose等。虽然numpy里面有可以直接使用的接口,能够实现这些功能,但是使用enisum可以做的更快、更节省空间。
举例说明,我们现在有两个矩阵A和B。我们想计算A和B的哈达玛乘积(即逐元素乘积),然后按行求和。
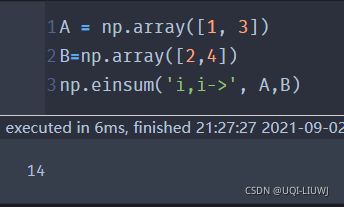
import numpy as np A = np.array([0, 1, 2]) B = np.array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])如果我们不适用einsum的话,也不是不能计算,就是需要写几步来完成:
A.reshape(-1,1) ''' array([[0], [1], [2]]) ''' A.reshape(-1,1)*B ''' array([[ 0, 0, 0, 0], [ 4, 5, 6, 7], [16, 18, 20, 22]]) ''' (A.reshape(-1,1)*B).sum(axis=1) #array([ 0, 22, 76])如果我们使用einsum的话,一行就可以实现:
np.einsum('i,ij->i', A, B) #array([ 0, 22, 76])
2 einsum原理
使用einsum的关键是,正确地labelling(标记)输入数组和输出数组的axes(轴)。
我们可以使用字符串(比如:ijk,这种表示方式更常用)或者一个整数列表(比如:[0,1])来标记axes。
比如,为了实现矩阵乘法,我们可以用einsum这么写(至于为什么这个是矩阵乘法,我们在后面会说明)
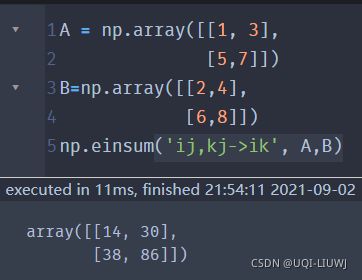
np.einsum('ij,jk->ik', A, B)字符串'ij,jk->ik'可以根据'->'的位置来切分,左边的部分('ij,jk')标记了输入的axes,右边的('ik')标记了输出的axes。
输入标记又根据','的位置进行切分,'ij'标记了第一个输入A的axes,'jk'标记了第二个输入B的axes。
'ij'、'jk'的字符长度都是2,对应着A和B为2D数组,'ik'的长度也为2,因此输出也是2D数组。
给定输入
A = np.array([[1, 3, 5],
[7, 9, -7],
[-5, -3, -1]])
B = np.array([[0, 2,4],
[6, 8, 6],
[4, 2, 0]])np.einsum('ij,jk->ik', A, B)可以看作是:
- 在输入数组的标记之间,重复字母表示沿这些轴的值将相乘,这些乘积构成输出数组的值。比如图中沿着j轴做乘积。
- 从输出标记中省略的字母表示沿该轴的值将被求和。比如图中的输出没有包含j轴,因此沿着j轴求和得到了输出数组中的每一项。
-
如果输出的标记是'ijk',那么会得到一个 3x3x3 的矩阵。
A = np.array([[1, 3, 5], [7, 9, -7], [-5, -3, -1]]) B = np.array([[0, 2,4], [6, 8, 6], [4, 2, 0]]) np.einsum('ij,jk->ijk', A, B) ''' array([[[ 0, 2, 4], [ 18, 24, 18], [ 20, 10, 0]], [[ 0, 14, 28], [ 54, 72, 54], [-28, -14, 0]], [[ 0, -10, -20], [-18, -24, -18], [ -4, -2, 0]]]) ''' -
输出标记是'ik'的时候,并不会创建中间的 3x3x3 的矩阵,而是直接将总和累加到2D数组中。
A = np.array([[1, 3, 5], [7, 9, -7], [-5, -3, -1]]) B = np.array([[0, 2,4], [6, 8, 6], [4, 2, 0]]) np.einsum('ij,jk->ik', A, B) ''' array([[ 38, 36, 22], [ 26, 72, 82], [-22, -36, -38]]) '''
如果输出的标记是空,那么输出整个矩阵的和
A = np.array([[1, 3, 5], [7, 9, -7], [-5, -3, -1]]) B = np.array([[0, 2,4], [6, 8, 6], [4, 2, 0]]) np.einsum('ij,jk->', A, B) #180
我们可以按任意顺序排序不求和的轴。
A = np.array([[1, 3, 5], [7, 9, -7], [-5, -3, -1]]) B = np.array([[0, 2,4], [6, 8, 6], [4, 2, 0]]) np.einsum('ij,jk->kji', A, B) ''' array([[[ 0, 0, 0], [ 18, 54, -18], [ 20, -28, -4]], [[ 2, 14, -10], [ 24, 72, -24], [ 10, -14, -2]], [[ 4, 28, -20], [ 18, 54, -18], [ 0, 0, 0]]]) '''
3 einsum分析
3.1 'ij,jk->ijk' 与 'ij,jk->kji'
我们一个一个分析一下
A = np.array([[1, 3, 5],
[7, 9, -7],
[-5, -3, -1]])
B = np.array([[0, 2,4],
[6, 8, 6],
[4, 2, 0]])
np.einsum('ij,jk->ijk', A, B)
'''
array([[[ 0, 2, 4],
[ 18, 24, 18],
[ 20, 10, 0]],
[[ 0, 14, 28],
[ 54, 72, 54],
[-28, -14, 0]],
[[ 0, -10, -20],
[-18, -24, -18],
[ -4, -2, 0]]])
'''首先,这几个数字是怎么得到的?
| 0=1*0 | 2=1*2 | 4=1*4 |
| 18=3*6 | 24=3*8 | 18=3*6 |
| 20=5*4 | 10=5*2 | 0=5*0 |
| 0=7*0 | 14=7*2 | 28=7*4 |
| 54=9*6 | 72=9*8 | 54=9*6 |
| -28=-7*4 | -14=-7*2 | 0=-7*0 |
| 0=-5*0 | -10=-5*2 | -20=-5*4 |
| -18=-3*6 | -24=-3*8 | -18=-3*6 |
| -4=-1*4 | -2=-1*2 | 0=-1*0 |
转换成坐标,有:
| [0,0]*[0,0] | [0,0]*[0,1] | [0,0]*[0,2] |
| [0,1]*[1,0] | [0,1]*[1,1] | [0,1]*[1,2] |
| [0,2]*[2,0] | [0,2]*[2,1] | [0,2]*[2,2] |
| [1,0]*[0,0] | [1,0]*[0,2] |
[1,0]*[0,4] |
| [1,1]*[1,0] | [1,1]*[1,1] | [1,1]*[1,2] |
| [1,2]*[2,0] | [1,2]*[2,1] | [1,2]*[2,2] |
| [2,0]*[0,0] | [2,0]*[0,1] | [2,0]*[0,2] |
| [2,1]*[1,0] | [2,1]*[1,1] | [2,1]*[1,2] |
| [2,2]*[2,0] | [2,2]*[2,1] | [2,2]*[2,2] |
A = np.array([[1, 3, 5],
[7, 9, -7],
[-5, -3, -1]])
B = np.array([[0, 2,4],
[6, 8, 6],
[4, 2, 0]])
np.einsum('ij,jk->kji', A, B)
'''
array([[[ 0, 0, 0],
[ 18, 54, -18],
[ 20, -28, -4]],
[[ 2, 14, -10],
[ 24, 72, -24],
[ 10, -14, -2]],
[[ 4, 28, -20],
[ 18, 54, -18],
[ 0, 0, 0]]])
'''与上面类似,我们就看第一个3*3的矩阵吧
| 0=1*0 | 0=7*0 | 0=-5*0 |
| 18=3*6 | 54=9*6 | -18=-3*6 |
| 20=5*4 | -28=-7*4 | -4=-1*4 |
| [0,0]*[0,0] | [1,0]*[0,0] | [2,0]*[0,0] |
| [0,1]*[1,0] | [1,1]*[1,0] | [2,1]*[1,0] |
| [0.2]*[2,0] | [1,2]*[2,0] | [2,2]*[2,0] |
可以这么考虑 对于 结果矩阵(比如ijk),第【i,j,k】元素的结果等于【i,j】乘以【j,k】
3.2 'ij,jk->ik'
A = np.array([[1, 3, 5],
[7, 9, -7],
[-5, -3, -1]])
B = np.array([[0, 2,4],
[6, 8, 6],
[4, 2, 0]])
np.einsum('ij,jk->ik', A, B)
'''
array([[ 38, 36, 22],
[ 26, 72, 82],
[-22, -36, -38]])
'''我们前面 'ij,jk->ijk'的结果是
| 0=1*0 | 2=1*2 | 4=1*4 |
| 18=3*6 | 24=3*8 | 18=3*6 |
| 20=5*4 | 10=5*2 | 0=5*0 |
| 0=7*0 | 14=7*2 | 28=7*4 |
| 54=9*6 | 72=9*8 | 54=9*6 |
| -28=-7*4 | -14=-7*2 | 0=-7*0 |
| 0=-5*0 | -10=-5*2 | -20=-5*4 |
| -18=-3*6 | -24=-3*8 | -18=-3*6 |
| -4=-1*4 | -2=-1*2 | 0=-1*0 |
这边相当于
| 38=0+18+20 | 36=2+24+10 | 22=4+18 |
| 26=54-28 | 72=14+72-14 | 82=54+28 |
| -22=-18-4 | -36=-10-24-2 | -38=-20-18 |
可以这么考虑 对于 结果矩阵(比如ik),第【i,k】元素的结果等于:对所有的j,【i,j】乘以【j,k】的结果的和
4 常用的Einsum
4.1 向量篇
| ('i',A) | 向量A的一个视图 可以看成'i->i',即结果的第i位,是A的第i位 |
| ('i->', A) | sum(A) 可以看成'i->0',即结果的第0位,是A的第i位的和 |
| ('i,i->i', A,B) | 向量A,B对应位置相乘 'i,i->i':结果的第i位,是A和B的第i位的积 |
| ('i,i->', A,B) | 向量A,B的内积 'i,i->':可以看成'i,i->0' 结果的第0位,是A和B的第i位的积 再求和 |
| ('i,j->ij', A,B) | 向量A,B的外积 'i,j->ij':结果的第i行第j列,是A的第i个元素和B的第j个元素的乘积 |
4.2 矩阵篇
| ('ij', A) | 返回矩阵A 看成'ij->ij' ,结果的第i行第j列,是A的第i行第j列 |
| ('ji->ij', A) | 返回矩阵A的转置 结果的第i行第j列的元素是A的第j行第i列的元素 |
| ('ii->i', A) | 矩阵A的对角线元素 结果的第i个元素是A的第i行第i列的元素 |
| ('ij->', A) | 矩阵A的元素之和 可以看成'ij->0' 结果的第0位是A的第i行第j列的元素,再求和 |
| ('ij->j', A) | A纵向求和 结果的第j个元素是,对所有的i,A的第(i,j)个元素的和 |
| ('ij->i', A) | A横向求和 结果的第i个元素是,对所有的j,A的第(i,j)个元素的和 |
| ('ij,ij->ij', A,B) | 矩阵A,B相应位置的乘积 结果第i,j个元素,是A的第(i,j)个元素和B的第(i,j)个元素的乘积 |
| ('ij,ji->ij', A,B) | 矩阵A和 矩阵B的转置 相应位置的乘积 结果第i,j个元素,是A的第(i,j)个元素和B的第(j,i)个元素的乘积 |
| ('ij,jk->ik', A,B) | A,B的矩阵乘积 结果的第(i,k)个元素等于A的第(i,j)个元素乘以B的第(j,k)个元素 |
| ('ij,kj->ik', A,B) | 矩阵A和矩阵B的内积 |
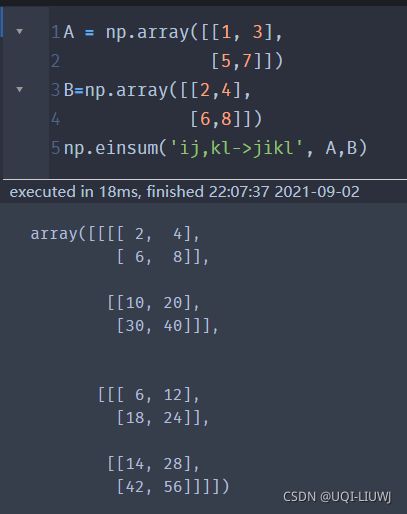
| ('ij,kl->jikl', A,B) | A的每个元素乘以矩阵B 结果的 第(j,i,k,l)个元素是A的(i,j)和B的(k,l)的乘积 |
| ('dn,nd->',A,B) | 相当于tr(AB) |
5 显示表明和隐式表明
我们将指定'->'和输出标记称为 explicit mode。
如果不指定'->'和输出标记,numpy会将输入标记中只出现一次的标记按照字母表顺序,作为输出标记(也就是 implicit mode)。
'ij,jk->ik' 等价于 'ij,jk'
参考文章:einsum初探 - 知乎 (zhihu.com)