递归实现指数型、排列型和组合型枚举

1、递归实现指数型枚举

从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 n。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1≤n≤15

输入样例：

3

输出样例：

3
2
2 3
1
1 3
1 2
1 2 3

题目分析

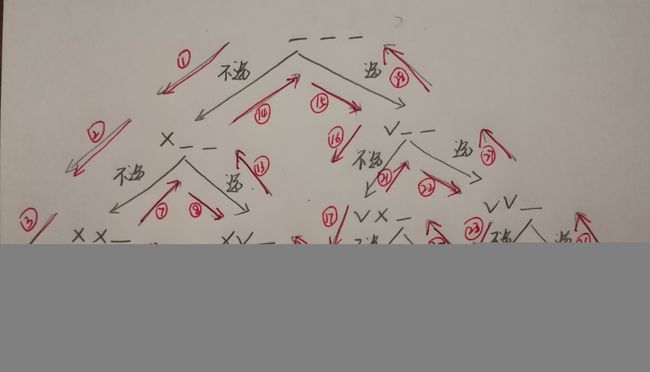
n个数随机选取任意多个，则最多选取n个，最少选取0个，可以这样想，n个数可以设置n个位置，第i个位置代表第i个数，每个位置的数据都有被选中和不被选中两种状态，则根据此我们可以画出该问题求解的递归搜索树，具体如下图所示（以输入n为3位例）：

       图中叉号表示不选，对号表示选中，红色标注为运行时对应的步骤（图片手绘，略有潦草）

       对于图中的选与不选，我们设置一个状态数组st[N]（N=n+1，因为数组有0号元素，也即数组下标从0开始，我们开辟n+1个空间大小的数组则可以让数组下标i和第i个数据一一对应）；则st[i]则可以来标记该数据是否被选入，具体设置如下：

（1）st[i]=0   代表还未处理到第i个数

（2）st[i]=1   代表第i个数被选入

（3）st[i]=2   代表第i个数未被选入

       并且每次我们递归到树叶时（也即找到递归出口时）代表已经寻找出一种选择方案，此时我们从第1个数到第n个数依次判断其对应的状态数组中的内容是否为1，为1 则代表选中，输出，否则不输出，这种输出方式则保证了每种选择方案都是按照升序排列。

说明

（1）将变量定义在函数外边不赋初值时，则程序默认初始化为0；当将变量定义在主函数内部时若给其赋初值则程序默认初始化为随机数。

程序代码示例

#include
using namespace std;
const int N=16;
int st[N];
int n;
void dfs(int u){
    if(u>n){       //程序递归出口
    //每次递归找到出口也即到达叶子结点，则代表一种选择方案的生成
    //从1到n依次判断其对应的状态数组内容来输出
        for(int i=1;i<=n;i++)
        {   if(st[i]==1)//当状态数组内容为1时表示选中该数据，则输出
            printf("%d ",i);
        }
     //每种选择方案结束后回车换行
            printf("\n");
            return;//注意函数为不带参数返回，所以return后面什么都不能写
    }
    st[u]=2;//进入左分支：每次向下递归都是先考虑当前位置的数据不选，状态数组设置为2
    dfs(u+1);
    st[u]=0;//每次递归后都要恢复现场
    
    st[u]=1;//进入右分支：当前位置数据选入，状态数组对应内容标记为1
    dfs(u+1);
    st[u]=0;//每次递归后都要恢复现场
}

int main(){
    cin>>n;
    dfs(1);//刚开始从第一个数据的选择开始逐步向下递归
    return 0;
}

2、递归实现排列型枚举

把 1∼n 这 n个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入格式

一个整数 n。

输出格式

按照从小到大的顺序输出所有方案，每行 1个。

首先，同一行相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一 一比较，字典序较小的排在前面。

数据范围

1≤n≤9

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

题目分析

n个数据进行全排列，并要求字典序小的排在前面，可以从第一个位置到第n个位置依次枚举每一位置上应该放置哪一个数。当然全排列要求的是每一个数只能出现一次，因此需要用标志数组来记录该数据是否已经选用，此处设置为ways[N],当值为true时表示已经选用，当值为false时表示该数字还没有被选中。同前面指数型枚举类似，当达到叶子结点时到达递归出口，也即选择第n个数结束时，因为每一层进行一个位置数据的选择。

程序代码示例

#include
using namespace std;
const int N=16;
//全局变量初值为0，局部变量初值随机
int state[N];//定义状态数组，state[i]里面存的是第i个数字的值
int n;
bool ways[N];//布尔类型数组，用来标志该数字是否已经被选中
//值为false表示未选中，值为true表示选中
void dfs(int u){
    if(u>n){//终止条件，到达叶子结点时
        for(int i=1;i<=n;i++)
        printf("%d ",state[i]);
        printf("\n");
        return;
    }
    for(int i=1;i<=n;i++){
        if(!ways[i]){//按照数组下标的顺序来判断元素是否已经被选中，
//也即优先选取数值小的元素，如此可以保证按照字典序排列
            state[u]=i;
            ways[i]=true;
            dfs(u+1);
            state[u]=0;//每次递归结束后都要恢复现场
            ways[i]=false;//恢复现场
        }
    }
}
int main()
{
    scanf("%d",&n);
    dfs(1);
    return 0;
}

3、递归实现组合型枚举

从 1∼n 这 n 个整数中随机选出 m个，输出所有可能的选择方案。

输入格式

两个整数 n,m,在同一行用空格隔开。

输出格式

按照从小到大的顺序输出所有方案，每行 1个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围

n>0，0≤m≤n ,n+(n−m)≤25

输入样例：

5 3

输出样例：

1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5 

 

#include
#include
#include
#include

using namespace std;
int const N=30;
int m,n,ways[N];
void dfs(int u,int start){
    if(u==m+1){
        for(int i=1;i<=m;i++){
            printf("%d ",ways[i]);
        }
        printf("\n");
        return;
    }
    for(int i=start;i<=n;i++){
        ways[u]=i;
        dfs(u+1,i+1);
        ways[u]=0;
    }
}

int main(){
    cin>>n>>m;
    dfs(1,1);
    return 0;
}