核函数+支持向量机+SMO算法详解

核函数

一、核心思想

在前面我们所讨论的分类器中，基本都是线性分类器，但是当数据集不存在一个线性的决策边界时，线性分类器便无法很好得进行分类。
事实证明，有一种优雅的方法可以将非线性问题合并到大多数的线性分类器可解决的问题中，即将线性分类器非线性化，这便是核函数。

我们可以看一个经典的例子：如下图所示的数据集，显然它是不存在线性的决策边界的，但是我们可以通过函数$\varphi$对特征向量进行特征变换使得数据线性可分。

我们不妨将特征变换函数定义为：
$$\varphi (x)=\varphi ([x_1,x_2{]}^T)=[x_1,x_2,|x_1\cdot x_2|{]}^T$$
我们所添加的维度捕捉了原始特征之间的非线性交互，使得数据变为了线性可分，升维的方法较为简便，并且使得问题保持凸且表现良好，但是缺点是升维可能会导致维度过高，使得模型变得复杂，比如下面这个例子所示：

通过特征变换，维度从$d$维变为了$2^d$维，这种新的表示法$\varphi (x)$非常有表现力，允许复杂的非线性决策边界，但维数非常高。这使得我们的算法速度慢得令人无法忍受。

二、核技巧

核技巧是一种通过在更高维空间中学习函数来绕过这一困境的方法，而无需计算单个向量$\varphi (x)$或完整向量$w$。

2.1 梯度下降

我们考虑平方损失函数的梯度下降过程：
$$l(w)=\sum _{i=1}^n(w^T{x}_i-y_i{)}^2$$
在梯度下降过程中，我们每次需要选择一个步长进行更新：
$$\begin{gathered} w_{t+1}=w_t-s\cdot (\frac{\partial l(w)}{\partial w}) \\ \frac{\partial l(w)}{\partial w}=2\sum _{i=1}^n(w^T{x}_i-y_i)\cdot x_i \end{gathered}$$
此处我们要引入一个重要的假设：我们可以将参数$w$表示为特征向量$x_i$的线性组合：
$$w=\sum _{i=1}^n{\alpha }_i{x}_i$$
根据该假设我们可以得到：$w_{t+1}$与$x_i$线性相关，$w_t$与$x_i$线性相关，由此：梯度$\frac{\partial l(w)}{\partial w}$与$x_i$线性相关：
$$\frac{\partial l(w)}{\partial w}=2\sum _{i=1}^n(w^T{x}_i-y_i)\cdot x_i=\sum _{i=1}^n{\gamma }_i{x}_i$$
由于损失函数为凸函数，最终解与初始化无关我们可以将$w_0$初始化为我们想要的任何值，我们不妨令：
$$w_0=[0,0,...,0{]}^T,{\alpha }^0=[0,0,...,0{]}^T$$
根据上述分析我们可以得到梯度下降的过程为：
$$\begin{array}{rl}& w_1=w_0-s\cdot 2\sum _{i=1}^n(w_0^T{x}_i-y_i)x_i=\sum _{i=1}^n{\alpha }_i^0{x}_i-s\sum _{i=1}^n{\gamma }_i^0{x}_i=\sum _{i=1}^n{\alpha }_i^1{x}_i{\alpha }^1={\alpha }^0-s{\gamma }^0\\ & w_2=w_1-s\cdot 2\sum _{i=1}^n(w_1^T{x}_i-y_i)x_i=\sum _{i=1}^n{\alpha }_i^1{x}_i-s\sum _{i=1}^n{\gamma }_i^1{x}_i=\sum _{i=1}^n{\alpha }_i^2{x}_i{\alpha }^2={\alpha }^1-s{\gamma }^1\\ & w_3=w_2-s\cdot 2\sum _{i=1}^n(w_2^T{x}_i-y_i)x_i=\sum _{i=1}^n{\alpha }_i^2{x}_i-s\sum _{i=1}^n{\gamma }_i^2{x}_i=\sum _{i=1}^n{\alpha }_i^2{x}_i{\alpha }^3={\alpha }^2-s{\gamma }^2\\ & ...\\ & w_t=w_{t-1}-s\cdot 2\sum _{i=1}^n(w_{t-1}^T{x}_i-y_i)x_i=\sum _{i=1}^n{\alpha }_i^{t-1}{x}_i-s\sum _{i=1}^n{\gamma }_i^{t-1}{x}_i=\sum _{i=1}^n{\alpha }_i^t{x}_i{\alpha }^t={\alpha }^{t-1}-s{\gamma }^{t-1}\end{array}$$
因为${\alpha }_i^0=0$，则有：
$$\begin{array}{rl}& {\alpha }_i^1=0-s{\gamma }_i^0=-s{\gamma }_i^0\\ & {\alpha }_i^2={\alpha }_i^1-s{\gamma }_0^1=-s{\gamma }_i^0-s{\gamma }_i^1\\ & {\alpha }_i^3={\alpha }_i^2-s{\gamma }_i^2=-s{\gamma }_i^0-s{\gamma }_i^1-s{\gamma }_i^2\\ & ...\\ & {\alpha }_i^t={\alpha }_i^{t-1}-s{\gamma }_i^{t-1}=-s\sum _{r=1}^{t-1}{\gamma }_i^r\end{array}$$
我们用$x_i$的线性组合代替$w$，得到新的模型和损失函数：
$$\begin{gathered} h(x_i)=w_t^T{x}_i=\sum _{j=1}^n{\alpha }_j^t{x}_j^T{x}_i \\ l(w)=\sum _{i=1}^n(w_t^T{x}_i-y_i{)}^2=\sum _{i=1}^n(\sum _{j=1}^n{\alpha }_j^t{x}_j^T{x}_i-y_i{)}^2 \end{gathered}$$
由此我们可以发现：为了学习具有平方损失的超平面分类器，我们需要的唯一信息是所有数据的特征向量对之间的内积。

2.2 计算内积

有了上述推导，我们将模型简化为只需要求解向量对之间的内积，我们回归到上述的升维操作中去：

在升维之后，内积的计算公式为：
$$\varphi (x{)}^T\varphi (z)=1+x_1{z}_1+x_2{z}_2+...x_1{x}_2...x_d{z}_1{z}_2...z_d=\prod _{k=1}^d(1+x_k{z}_k)$$
我们可以发现，尽管特征向量是$2^d$维的，但是计算其内积仅需要$d$次乘法运算，这极大提高了算法的速度。

我们由此即可定义核函数：
$$k(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$$
核函数计算出的结果存储在核矩阵中：
$$K_{ij}=\varphi (x_i{)}^T\varphi (x_j)$$
诸如$\varphi$之类的用于升维的映射并不好找，因此我们用核函数$k(x_i,x_j)$去代替这样的映射，处理线性不可分问题。

则上述模型可以表示为：可以发现模型中唯一的未知参数即为$\alpha$，我们需要对它进行求解
$$h(x_i)=w^T{x}_i=\sum _{j=1}^n{\alpha }_j{x}_j^T{x}_i=\sum _{j=1}^n{\alpha }_{j}k(x_j,x_i)$$
同时我们也已经得到了：
$${\alpha }_i^t=-s\sum _{r=1}^{t-1}{\gamma }_i^r$$
所以当下我们的求解目标变为了$\gamma$：
$$\begin{gathered} \frac{\partial l(w)}{\partial w}=2\sum _{i=1}^n(w^T{x}_i-y_i)\cdot x_i=\sum _{i=1}^n{\gamma }_i{x}_i \\ {\gamma }_i=2(w^T{x}_i-y_i) \end{gathered}$$
在经过$\varphi$特征变换的新的高维空间中有：
$${\gamma }_i=2(w^T\varphi (x_i)-y_i)=2(\sum _{j=1}^n{\alpha }_{j}k(x_j,x_i)-y_i)$$
则梯度下降的过程为：
$${\alpha }_i^{t+1}={\alpha }_i^t-s{\gamma }_i^t={\alpha }_i^t-2s(\sum _{j=1}^n{\alpha }_j^{t}k(x_j,x_i)-y_i)$$
梯度下降过程中，每次更新$\alpha$的计算量为$O(n^2)$，远好于$O(2^d)$

三、一般核函数

3.1 常用核函数

（1）线性核函数：
$$K(x,z)=x^{T}z$$
（2）多项式核函数：
$$K(x,z)=(1+x^{T}z{)}^d$$
（3）高斯核函数（$\text{RBF}$）：
$$K(x,z)=e^{-\frac{||x-z|{|}_2^2}{{\sigma }^2}}$$
（4）指数核函数：
$$K(x,z)=e^{-\frac{||x-z||}{2{\sigma }^2}}$$
（5）拉普拉斯核函数：
$$K(x,z)=e^{-\frac{|x-z|}{\sigma }}$$
（6）$\text{Sigmoid}$核函数：$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
$$K(x,z)=\tanh (\gamma x^{T}z+r)$$

3.2 良定义核函数

良定义的核函数定义如下：通过递归组合以下一个或多个规则构建的核称为定义良好的核：
$$\begin{array}{rl}& ①k(x,z)=x^{T}z\\ & ②k(x,z)=c{k}_1(x,z)\\ & ③k(x,z)=k_1(x,z)+k_2(x,z)\\ & ④k(x,z)=g(k(x,z))\\ & ⑤k(x,z)=k_1(x,z)\cdot k_2(x,z)\\ & ⑥k(x,z)=f(x)k_1(x,z)f(z)\\ & ⑦k(x,z)=e^{k_1(x,z)}\\ & ⑧k(x,z)=x^{T}Az\end{array}$$
上述规则中$k_1(x,z)$和$k_2(x,z)$都是良定义的核函数，$c\ge 0$，$g$是一个正系数多项式函数，$f$是任何函数，$A$是半正定的

某个核函数是良定义的等价为：
①核矩阵$K$的特征值都是非负的
②存在实矩阵$P$使得：$K=P^{T}P$
③核矩阵$K$是半正定的，即对于任何向量$x$，都有：$x^{T}Kx\ge 0$

定理 3-1

$$\text{RBF}核函数：k(x,z)=e^{-\frac{(x-z{)}^2}{{\sigma }^2}}是良定义的$$

证明如下：
$$\begin{array}{rl}& k(x,z)=e^{-\frac{(x-z{)}^2}{{\sigma }^2}}=e^{-\frac{1}{{\sigma }^2}(x^{T}x-2x^{T}z+z^{T}z)}=e^{-\frac{x^{T}x}{{\sigma }^2}}\cdot e^{\frac{2x^{T}z}{{\sigma }^2}}\cdot e^{-\frac{x^{T}x}{{\sigma }^2}}\end{array}$$

$$\begin{array}{rl}& 根据规则⑥：f(x)=e^{-\frac{x^{T}x}{{\sigma }^2}},k_1(x,z)=e^{\frac{2x^{T}z}{{\sigma }^2}}\to k(x,z)=f(x)\cdot k_1(x,z)\cdot f(z)\\ & 根据规则⑦：k_2(x,z)=\frac{2x^{T}z}{{\sigma }^2}\to k_1(x,z)=e^{k_2(x,z)}\\ & 根据规则②：k_3(x,z)=x^{T}z,c=\frac{2x^{T}z}{{\sigma }^2}\to k_2(x,z)=c\cdot k_3(x,z)\\ & 根据规则①：k_3(x,z)\text{ is well defined}\to k_2(x,z)\text{ is well defined}\to k_1(x,z)\text{ is well defined}\end{array}$$

综上推导：
$$k(x,z)\text{ is well defined}$$

定理 3-2

$$S_1,S_2\in \Omega ,k(S_1,S_2)=e^{|S_1\cap S_2|}是良定义的$$

证明如下：

将$\Omega$中所有可能的元素排列成一个列表，$S_1,S_2$分别用一个大小为$|\Omega |$的向量$x^{S_1},x^{S_2}$表示，如果$\Omega$中的第$i$个元素属于$S$，则$x_i^S=1$，反之则$x_i^S=0$，则上述核函数可以表示为：
$$\begin{array}{rl}& k(S_1,S_2)=e^{x_{S_1}^T{x}_{S_2}}\end{array}$$
根据规则⑦和规则①，我们可以得到：$k(S_1,S_2)$为良定义核函数。

四、模型核化

一个算法可以通过三步实现核化：
①证明解决方案位于训练点的范围内，即对于某些${\alpha }_i$：
$$w=\sum _{i=1}^n{\alpha }_i{x}_i$$
②重构算法与分类器，使得输入的特征向量仅用于内积的计算
③将内积替换为核函数：
$$x_i^T{x}_j\to \varphi (x_i{)}^T\varphi (x_j)$$

4.1 线性回归核化

我们回顾一下普通的最小二乘回归$OLS$：
$$\begin{gathered} l(w)=\sum _{i=1}^n(x_i^{T}w-y_i) \\ {\hat{w}}_{MLE}=\underset{w}{\mathrm{argmin}}\sum _{i=1}^n(x_i^{T}w-y_i) \\ h(x)=w^{T}x \end{gathered}$$
输入的训练集为$X$和$Y$，则其闭合形式为：
$$w=(X^{T}X{)}^{-1}{X}^{T}Y$$
我们对该模型进行核化：$X$为$n\times d$维矩阵，$Y$为$n\times 1$维矩阵，$w,x_i$为$d\times 1$维矩阵，$\alpha$为$n\times 1$维矩阵
①将$w$表示为$x_i$的线性组合：$\alpha =[{\alpha }_1,{\alpha }_2,...,{\alpha }_n{]}^T$
$$\begin{array}{rl}& w=\sum _{i=1}^n{\alpha }_i{x}_i=X^T\alpha \end{array}$$
②将模型修正为输入特征向量的内积：
$$h(x_i)=\sum _{j=1}^n{\alpha }_j{x}_j^T{x}_i=w^T{x}_i={\alpha }^{T}X{x}_i$$
③用核函数代替内积：
$$h(x_i)=\sum _{j=1}^n{\alpha }_{j}k(x_j,x_i)$$
求解$\alpha$的闭合形式：
$$\begin{array}{rl}& w=X^T\alpha =(X^{T}X{)}^{-1}{X}^{T}Y\to X^{T}X{X}^T\alpha =X^{T}Y\to X{X}^T\alpha =Y\\ & K_{ij}=k(x_i,x_j)\to K=X{X}^T\to K\alpha =Y\\ & \alpha =K^{-1}Y\end{array}$$
岭回归同理，我们也可以实现同样的核化并求解$\alpha$的闭合形式：

模型为：
$$\begin{gathered} l(w)=\sum _{i=1}^n(x_i^{T}w-y_i)+\lambda ||w|{|}_2^2 \\ {\hat{w}}_{MAP}=\underset{w}{\mathrm{argmin}}\sum _{i=1}^n(x_i^{T}w-y_i)+\lambda ||w|{|}_2^2 \\ h(x)=\sum _{j=1}^n{\alpha }_{j}k(x_j,x_i) \end{gathered}$$
$\alpha$的闭合形式为：
$$\begin{array}{rl}& w=X^T\alpha =(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y\to (X^{T}X+\lambda I)X^T\alpha =X^{T}Y\\ & \to (X^{T}X{X}^T+\lambda X^T)\alpha =X^{T}Y\to (X{X}^T+\lambda I)\alpha =Y\\ & \to \alpha =(K+\lambda I{)}^{-1}Y\end{array}$$

4.2 KNN核化

我们以欧拉距离的$KNN$模型为例：
$$\text{dist}(x_i,x_j)=(x_i-x_j{)}^T(x_i-x_j)=x_i^T{x}_i-2x_i^T{x}_j+x_j^T{x}_j=k(x_i,x_i)-2k(x_i,x_j)+k(x_j,x_j)$$
但是上述核化的意义并不大，因此我们一般不对$KNN$算法进行核化。

4.3 支持向量机核化

线性支持向量机结合核函数是一个很强大的模型，我们往往求解其对偶问题，所以我们需要先了解对偶问题的定义。

4.3.1 拉格朗日乘子法与KKT条件

在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。

我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值，支持向量机模型即为该类最优化为问题。

在求解最优化问题时一般会遇到三种情况：

（1）无约束条件：
这是最简单的情况，解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。

（2）等式约束条件：
设目标函数为$f(x)$，约束条件为$h_k(x)$，有$l$个约束条件，则等式约束条件的最优化问题可以表示为：
$$\begin{array}{rl}& 求解目标：\min f(x)\\ & 约束条件：h_k(x)=0,k=1,2,...l\end{array}$$
我们要用到拉格朗日乘子法处理该最优化问题：首先定义拉格朗日函数：
$$F(x.\lambda )=f(x)+\sum _{k=1}^l{\lambda }_k{h}_k(x)$$
然后解变量的偏导方程：
$$\begin{gathered} \frac{\partial F(x,\lambda )}{\partial x_1}=0,\frac{\partial F(x,\lambda )}{\partial x_2}=0,...,\frac{\partial F(x,\lambda )}{\partial x_d}=0 \\ \frac{\partial F(x,\lambda )}{\partial {\lambda }_1}=0,\frac{\partial F(x,\lambda )}{\partial {\lambda }_2}=0,...,\frac{\partial F(x,\lambda )}{\partial {\lambda }_k}=0 \end{gathered}$$
（3）不等式约束条件：
设目标函数为$f(x)$，不等式约束条件为$g_k(x)$，有$q$个不等式约束条件，等式约束条件为$h_j(k)$，有$p$个等式约束条件：
$$\begin{array}{rl}& 求解目标：\min f(x)\\ & 约束条件：h_j(x)=0,j=1,2,...,p\\ & g_k(x)\le 0,k=1,2,...,q\end{array}$$
则我们可以定义不等式约束条件下的拉格朗日函数为：
$$L(x,\lambda ,\mu )=f(x)+\sum _{j=1}^p{\lambda }_j{h}_j(x)+\sum _{k=1}^q{\mu }_k{g}_k(x)$$
常用的方法是$KKT$条件：即最优值（局部最小值）必须满足以下条件：
$$\begin{array}{rl}& ①\frac{\partial L(x,\lambda ,\mu )}{\partial x}{|}_{x=x^{\ast }}=0\\ & ②h_j(x^{\ast })=0\\ & ③{\mu }_k{g}_k(x^{\ast })=0\end{array}$$

4.3.2 对偶问题的核化

我们首先回顾支持向量机的模型：为了便于计算我们引入一个常系数$\frac{1}{2}$
$$\begin{array}{rl}& 求解目标：(w,b)=\underset{w,b}{\mathrm{argmin}}\frac{1}{2}||w|{|}_2^2\\ & 约束条件：\forall i,y_i(w^T{x}_i+b)\ge 1\end{array}$$
则拉格朗日函数为：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}_2^2+\sum _{i=1}^n{\alpha }_i(1-y_i(w^T{x}_i+b))$$
根据$KKT$条件可得：
$$\begin{array}{rl}& \frac{\partial L(w,b,\alpha )}{\partial w}=w-\sum _{i=1}^n{\alpha }_i{y}_i{x}_i=0\\ & \frac{\partial L(w,b,\alpha )}{\partial b}=-\sum _{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
我们同时也知道，在$w,b$取得最优值时有：$y_i(w^T{x}_i+b)=1$满足了$KKT$条件

综上，我们可得：
$$\begin{array}{rl}& w=\sum _{i=1}^n{\alpha }_i{y}_i{x}_i\\ & \sum _{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
我们上述条件代入原式可得：
$$\begin{array}{rl}& (w,b)=\underset{w,b}{\mathrm{argmin}}\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^n{\alpha }_i-\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{y}_i{y}_j{x}_i^T{x}_j-b\cdot \sum _{i=1}^n{\alpha }_i{y}_i\\ & \to (w,b)=\underset{w,b}{\mathrm{argmin}}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$
由此我们得到了支持向量机模型的对偶问题：
$$\begin{array}{rl}& 求解目标：\alpha =\underset{\alpha }{\mathrm{argmax}}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\\ & 约束条件：\sum _{i=1}^n{\alpha }_i{y}_i=0\end{array}$$
显然我们可以对该对偶问题进行核化：
$$\alpha =\underset{\alpha }{\mathrm{argmax}}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(x_i,x_j)$$
最终的模型为：
$$h(x)=\text{sign}(w^{T}x+b)=\text{sign}(\sum _{i=1}^n{\alpha }_i{y}_{i}k(x_i,x)+b)$$
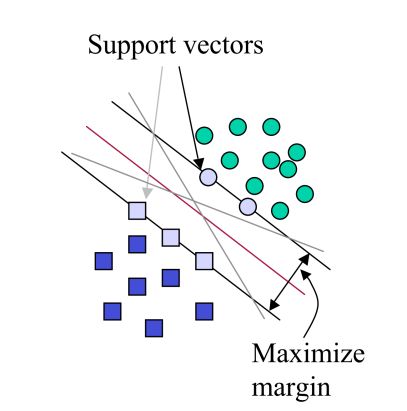
从支持向量的角度对对偶问题有一个很好的解释：对于原始公式，我们知道只有支持向量满足等式约束：
$$y_i(w^T\varphi (x_i)+b)=1$$
在对偶问题中我们可以使得支持向量所对应的${\alpha }_i>0$，而其他的输入向量对应的${\alpha }_i=0$，在测试时我们只需要计算支持向量上$h(x)$的和，并在训练后丢弃所有${\alpha }_i=0$的特征向量。

对偶有一个明显的问题，就是$b$不再是优化的一部分了，但是我们需要它来进行分类，在对偶中支持向量是那些${\alpha }_i>0$的向量，因此我们可以推导出$b$：
$$\begin{array}{rl}& y_i(w^T\varphi (x_i)+b)=1,y_i\in \{-1,+1\}\to b=y_i-w^T\varphi (x_i)\\ & \to b=y_i-\sum _{j=1}^n{\alpha }_j{y}_{j}k(x_j,x_i)\end{array}$$
同时如果使用软间隔模型，则仅需添加一个新的约束：
$$0\le {\alpha }_i\le C$$

由于正文字数限制，模型的实现原码和SMO算法就去掉了，可以查阅我的个人博客文章 核函数，这里有详细的原码与算法解析！