基于混合策略改进的鲸鱼优化算法

一、理论基础

1、鲸鱼优化算法

请参考这里。

2、改进的鲸鱼优化算法

（1）引入非线性递减收敛因子

原始的收敛因子$a$是按照固定速率下降，在算法迭代过程中不能很好的适应种群情况，一旦在探索阶段没有找到种群最优解，则在利用阶段很容易陷入局部最优，降低了算法的寻优精度。因此，本文采用两种非线性递减收敛因子结合随机参数的策略来控制算法执行过程中不同阶段的切换，具体的计算公式如下：$$a=\{\begin{array}{l}2-\frac{3}{2}\sqrt{e^{\frac{t}{T_{\max }}}-1},ran{d}_1\le P_a\\ 2{\left(\frac{t}{T_{\max }}\right)}^2-\frac{4t}{T_{\max }}+2,ran{d}_1>P_a\end{array}\text{\hspace{1em}(1)}$$$$A=2ar-a\text{\hspace{1em}(2)}$$其中，$t$为当前迭代数；$T_{\max }$为最大迭代次数；$P_a$代表收敛因子指数递减的概率，$P_a\in [0,1]$；$ran{d}_1$为$[0,1]$范围内的随机数，$ran{d}_1$的取值决定了收敛因子按不同的方式递减；$r$为$[0,1]$范围内的随机向量。设$T_{\max }=500$，则式(1)中两种曲线的变化趋势如图1所示。

图1 两种非线性递减收敛因子的变化趋势

由图1可知，在算法迭代的过程中，两种非线性收敛因子的递减情况具有不同的针对性。当以指数形式递减时，因子$a$的收敛速度会更加平缓，使算法能够在较长时间内进行全局搜索，降低了当前种群中最优个体对其他个体的影响，优化了下一代的种群质量。当收敛因子 a在多项式时间内递减时，算法会更快地进入到利用阶段，从而提高了局部收敛的速度，从整体上提升了算法的性能。为了使算法能够更好地平衡探索阶段和利用阶段，通过设置合适的$P_a$值来控制收敛因子的递减方式，以实现在最佳时机进行不同阶段间的切换。
设$P_a=0.6$，代表在算法执行初期，种群中的个体选择全局搜索的可能性更大，维护了种群的多样性，增强了算法的全局寻优能力。同时，在算法执行后期，也能随机地跳出局部最优，进一步扩大搜索范围，避免算法出现“早熟”现象。

（2）最优局部抖动

在捕食期间，鲸鱼容易受到种群中最优个体的影响，并逐渐靠近最优个体。但是，在算法的整个迭代过程中，只有出现比当前最优个体适应度更高的个体时，才会替换当前的最优个体。因此，最优个体一般保持不变，从而限制了算法的搜索范围。针对这种情况，将最优局部抖动思想融入鲸鱼优化算法中，在最优个体附近进行小范围的随机搜索，找到一个适应度值更高的个体，这样不仅有助于加快算法的全局收敛，还能避免算法过早地陷入局部最优。
最优个体在邻域内产生局部抖动的公式为：$$X^{\prime \ast }(t)=\{\begin{array}{l}{X}^{\ast }(t)+ran{d}_2\times X^{\ast }(t),ran{d}_2<0.5\\ X^{\ast }(t),ran{d}_2\ge 0.5\end{array}\text{\hspace{1em}(3)}$$其中，$ran{d}_2$为$[0,1]$区间上的随机数；$X^{\ast }(t)$是当前鲸鱼群中最佳鲸鱼的位置向量；$X^{\prime \ast }(t)$是优化后的新个体。
对于邻域内生成的新个体，采用贪心思想进行判断，具体模型如下：$$X^{\ast }(t)=\{\begin{array}{l}{X}^{\prime \ast }(t),f(X^{\prime \ast })<f(X^{\ast })\\ X^{\ast }(t),f(X^{\prime \ast })\ge f(X^{\ast })\end{array}\text{\hspace{1em}(4)}$$其中，$f(x)$为适应度函数。若新个体的适应度值优于原最优个体，则进行最优个体的替换；否则，继续保留原最优个体，不进行任何操作。

（3）动态位置更新

为了实现在迭代过程中鲸鱼能够依据外界情况动态地更新自身位置，引入自适应螺旋参数，将$b$设置成动态值，并依赖于迭代次数。随着迭代次数的增加，$b$值相应地进行变动，随机地改变螺旋路径，从而扩大鲸鱼的搜寻空间，进一步提升算法在种群范围内的搜索能力。动态螺旋位置更新公式如下：$$\{\begin{array}{l}X(t+1)=D^{\prime }\times e^{bl}\times \cos (2\pi l)+X^{\ast }(t)\\ b=1-\frac{5}{l}\cos \left(\frac{\pi t}{T_{\max }}\right)\end{array}\text{\hspace{1em}(5)}$$ D → ′ = ∣ X → ∗ ( t ) − X → ( t ) ∣ (6) \overrightarrow D'=\left|\overrightarrow X^*(t)-\overrightarrow X(t)\right|\tag{6} D ′= ​X ∗(t)−X (t) ​(6)其中，$X$是鲸鱼的当前位置向量；$D^{\prime }$表示当前鲸鱼与最佳鲸鱼之间的距离；$l$是$[-1,1]$区间上的随机数。
参数$b$的设计是在螺旋线方程的基础上引入了迭代次数，通过迭代次数的改变，螺线形状会动态地进行调整。在迭代初期，螺线形状偏大，鲸鱼能够在较大的范围内进行搜索，尽可能多地遍历种群中的个体，强化了算法全局寻优的能力；在迭代后期，螺线形状偏小，鲸鱼会在最优个体的附近进行搜索，从而加快了算法的收敛速度，同时保证算法具有良好的寻优精度。

（4）改进算法的执行流程

基于改进鲸鱼优化算法IWOA的流程如图2所示。

图2 基于改进鲸鱼优化算法的流程

二、仿真实验与结果分析

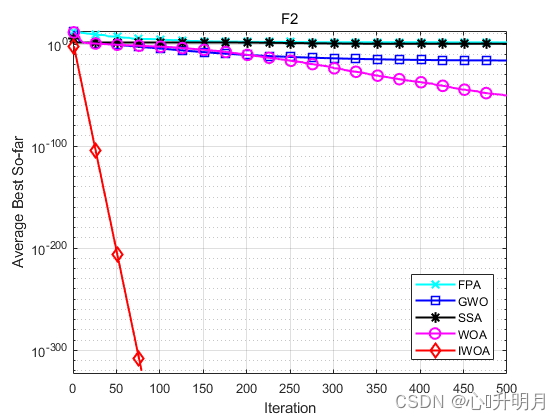
将IWOA与FPA、GWO、SSA和WOA进行对比，以常用23个测试函数中的F1、F2(单峰函数/30维)、F8、F9(多峰函数/30维)、F20、F21(固定维度多峰函数/6维、4维)为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

函数：F1
FPA：最差值: 3108.4371,最优值:868.6111,平均值:1756.2826,标准差:408.6132
GWO：最差值: 4.7674e-27,最优值:3.7363e-29,平均值:6.9861e-28,标准差:9.6087e-28
SSA：最差值: 2.5438e-06,最优值:2.4421e-08,平均值:2.0213e-07,标准差:4.6072e-07
WOA：最差值: 5.0954e-71,最优值:4.7616e-88,平均值:1.7267e-72,标准差:9.2987e-72
IWOA：最差值: 0,最优值:0,平均值:0,标准差:0
函数：F2
FPA：最差值: 76.6997,最优值:31.7315,平均值:54.7786,标准差:12.0864
GWO：最差值: 3.0641e-16,最优值:2.3872e-17,平均值:9.8735e-17,标准差:6.6335e-17
SSA：最差值: 7.7509,最优值:0.2084,平均值:1.9966,标准差:1.8455
WOA：最差值: 5.1065e-50,最优值:1.0124e-56,平均值:4.6679e-51,标准差:1.1581e-50
IWOA：最差值: 0,最优值:0,平均值:0,标准差:0
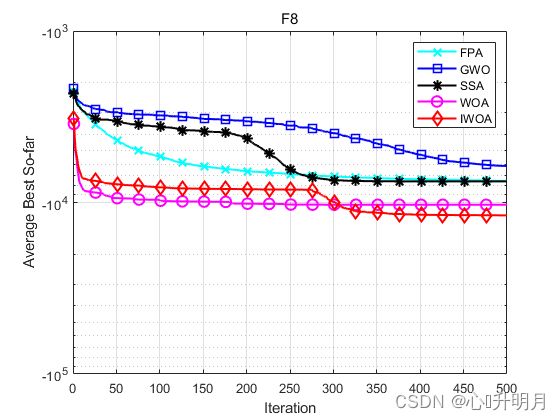
函数：F8
FPA：最差值: -7084.0801,最优值:-7984.9848,平均值:-7488.2818,标准差:221.1132
GWO：最差值: -4882.4057,最优值:-7444.8749,平均值:-6122.1715,标准差:722.1877
SSA：最差值: -6225.4352,最优值:-9049.4704,平均值:-7527.891,标准差:722.9383
WOA：最差值: -8091.5974,最优值:-12569.384,平均值:-10313.4192,标准差:1711.5483
IWOA：最差值: -6802.5895,最优值:-12569.4866,平均值:-11892.0026,标准差:1363.4078
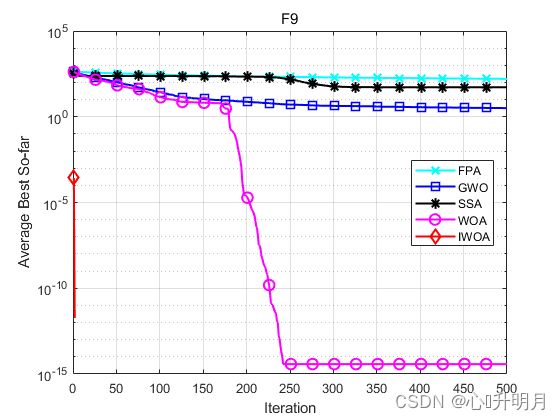
函数：F9
FPA：最差值: 197.7085,最优值:119.3235,平均值:162.4878,标准差:17.7884
GWO：最差值: 10.0776,最优值:5.6843e-14,平均值:3.2051,标准差:2.9298
SSA：最差值: 121.3845,最优值:19.8992,平均值:52.7659,标准差:23.1376
WOA：最差值: 5.6843e-14,最优值:0,平均值:3.7896e-15,标准差:1.4422e-14
IWOA：最差值: 0,最优值:0,平均值:0,标准差:0
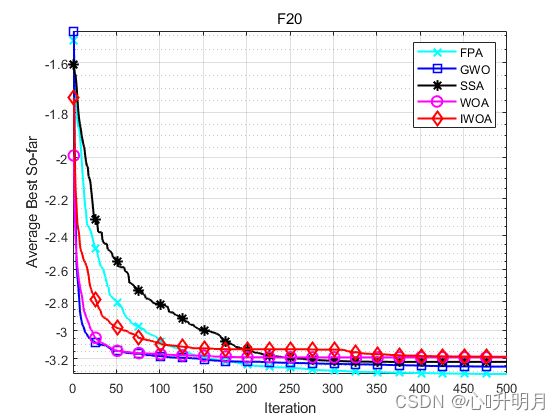
函数：F20
FPA：最差值: -3.2984,最优值:-3.3215,平均值:-3.3182,标准差:0.0044034
GWO：最差值: -3.1005,最优值:-3.322,平均值:-3.2618,标准差:0.079043
SSA：最差值: -3.1626,最优值:-3.322,平均值:-3.2254,标准差:0.060281
WOA：最差值: -2.4314,最优值:-3.3218,平均值:-3.1915,标准差:0.18075
IWOA：最差值: -2.4183,最优值:-3.3196,平均值:-3.1874,标准差:0.17652
函数：F21
FPA：最差值: -8.244,最优值:-10.116,平均值:-9.8115,标准差:0.37831
GWO：最差值: -2.6302,最优值:-10.1528,平均值:-8.6378,标准差:2.6132
SSA：最差值: -2.6305,最优值:-10.1532,平均值:-8.1487,标准差:3.1798
WOA：最差值: -2.6238,最优值:-10.1529,平均值:-8.1136,标准差:2.982
IWOA：最差值: -2.5896,最优值:-10.1531,平均值:-9.8386,标准差:1.3728

实验结果表明：改进算法比其他优化算法具有更高的寻优精度。

三、参考文献

[1] 蒋伟进, 张婉清, 陈萍萍, 等. 基于IWOA群智感知中数量敏感的任务分配方法[J]. 电子学报, 2022, 50(10): 2489-2502.