视觉slam基础知识
三维空间中刚体的运动描述方式
旋转矩阵、变换矩阵、欧拉角、四元数
旋转矩阵
空间中两个坐标系之间的旋转运动可由一个正交矩阵(行列式为1)表示,该矩阵称为旋转矩阵R。旋转矩阵的转置(=逆)表示了相反的旋转。
变换矩阵
空间中任意两个坐标系位置变换可分解为旋转+平移,因此有![]()
其中,R12:坐标系2到坐标系1的变换;t12:坐标系1的原点指向坐标系2的原点的向量。
变换矩阵T:
根据分块矩阵的转置计算T-1
欧拉角
用3个分离的转角表示一个旋转。一般用ZYX轴的旋转,偏航-俯仰-滚转,yaw-pitch-roll。用欧拉角描述旋转会出现万向锁问题,即当俯仰角pitch=90°时,第一次和第三次旋转使用的是同一轴,这将导致一个总旋转可以有多种欧拉角表示。
四元数
用纯虚四元数表示空间中的点p,旋转后的p’表示为
![]()
Eigen库的矩阵、几何模块的使用
C++学习笔记——Eigen模块(用于矩阵运算)_starvapour的博客-CSDN博客_eigen矩阵置零
注:如果要将一个大的Eigen矩阵的左上角3×3的块取出,然后赋值,可以使用.block()函数。
视觉SLAM十四讲第三章习题5_Uncertainty!!的博客-CSDN博客
- 李群和李代数
slam的核心问题是“什么样的相机位姿最符合当前观测数据”,这是一个优化问题,需要求解R和t,使误差最小化。
如果以旋转矩阵作为优化变量,则要求求解出来的矩阵必须是正交矩阵,这是一个带约束的优化问题。为将位姿估计变为无约束的优化问题,引入李群和李代数的概念。
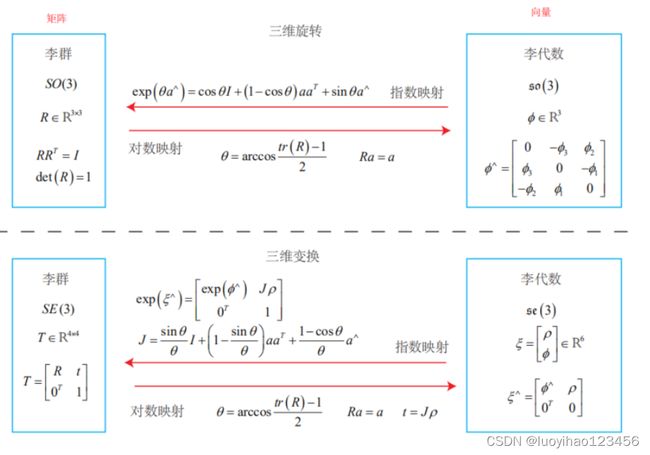
旋转矩阵SO(3)是特殊正交群,变换矩阵SE(3)是特殊欧式群,他们都是李群。
每一个李群都有一个李代数与之对应,李代数需要满足被称为李括号的二元运算。
![]()
R为李群,φ为李代数,也表示旋转向量。
注:当旋转角度固定在±π之间时,李群和李代数是一一对应的。
旋转矩阵和变换矩阵的导数由旋转向量(李代数)指定。
BCH公式建立起了李群乘法和李代数加法之间的桥梁。T为李群,![]() 为李代数,^指代从向量到矩阵的变换(6维向量变4维矩阵),ρ不直接是平移,满足
为李代数,^指代从向量到矩阵的变换(6维向量变4维矩阵),ρ不直接是平移,满足
t=J·ρ。
优化过程往往需要计算位姿关于变换矩阵的导数。
目前有两种思路:
1. 用李代数表示位姿,根据李代数的加法对李代数求导
2. 李群左乘微小扰动,然后对扰动求导(结果简单,更为实用)
绝对轨迹误差等于每个位姿李代数的均方根误差。
使用Sophus对李代数进行运算
Sophus在源码中自动将李群以李代数的形式输出。
参考:sophus库的一些使用_robinhjwy的博客-CSDN博客_sophus使用
相机与图像
针孔相机模型、内参和径向畸变参数
Z是深度,u、v是像素坐标,fx等于焦距乘以像素坐标在u轴上缩放的倍率α,cx等于像素坐标系下的原点与相机坐标系下原点在u轴方向上的距离。
单目相机的成像过程:
1. 世界坐标系下有一个固定点P,世界坐标系下为Pw;
2. 变换到相机坐标系下Pc=RPw+t;
3. 将相机坐标投影到归一化平面Z=1上,得到归一化坐标;
4. 有畸变时根据畸变参数计算畸变后的坐标;
5. 经过内参后,归一化坐标变为像素坐标
掌握OpenCV的图像存储与表达方式
参考:OpenCV基本操作 - Mister_HY - 博客园
非线性优化
持有当前时刻的估计状态,用新的数据进行更新,这种增量/渐进的方法称为滤波器。
将所有数据攒起来批量处理的方法称为批量的方法。
左侧表示在已知所有时刻的观测数据和输入时,机器人位姿和路标点坐标分别为x,y的概率,为后验概率(已知结果,求原因)。右侧第一项表示似然,即在已知机器人位姿和路标点坐标分别为x,y时,观测数据为z的概率,右侧第二项表示先验概率(已知原因,求结果)。
![]()
最大似然可理解为:若已知机器人位姿和路标点,求观测数据为多少时使得位姿和路标点的可能性最大。
最小二乘的含义和处理方法:
1. 给定某个初始值x0
2. 对于第k次迭代,寻找一个增量Δxk,使得函数达到极小值。
3. 若Δxk足够小,则停止。否则,令xk+1=xk+Δxk,返回第二步。
将求解导数为0的问题变为不断寻找下降增量Δxk的问题。
牛顿法
![]()
高斯牛顿法
![]()
列文伯格-马夸尔特方法
在高斯牛顿法中添加信赖区域,避免x过大使得二阶泰勒展开与原函数相差较大。
Ceres和g2o的使用
Ceres入门——Ceres的基本使用方法_Andy是个男子名的博客-CSDN博客_ceres
协方差矩阵
https://www.csdn.net/tags/MtjaIgysNjY1MjYtYmxvZwO0O0OO0O0O.html