数字图像处理（第三章 图像增强—灰度变换与空间滤波）
数字图像处理 知识总结
- 前言
- 第三章 图像增强—灰度变换与空间滤波
-
- 1 引言
-
- 图像增强的目的
- 空间域方法
- 变换域方法
- 2 灰度变换与空间滤波基础
- 3 基于灰度变换的图像增强
-
- 基本灰度变换函数
-
- 图像反转
- 对数变换
- 幂律(伽马)变换
- 分段线性变换函数
-
- 对比度拉伸
- 灰度级分层
- 直方图处理
-
- 直方图均衡化
-
- 连续函数均衡化;
- 离散函数的均衡化
- 直方 图规定化
- 局部直方图处理
- 4 基于空间滤波的图像增强
-
- 空间滤波基础
- 平滑空间滤波器（均值滤波器）
- 锐化空间滤波器
-
- 使用二阶微分图像锐化——拉普拉斯算子
- 使用一节微分图像锐化——梯度法
前言
参考书籍《数字图像处理》第四版 电子工业出版社。
第三章 图像增强—灰度变换与空间滤波
1 引言
图像增强的目的
对图像进行加工，使其结果比原始图像更适用于特定应用；是面向问题的。不同的问题增强方式不一定相同。
空间域方法
定义：这种方法对图像像素的直接处理，是相对于变换域图像处理而言；
空间域方法主要分为灰度变换和空间滤波两类
灰度变换在图像的单个像素上操作
主要以对比度和阈值处理为目的；
空间滤波在输入图像的邻域内进行一些涉及改善性能的操作。
例如，通过对图像中每一个像素的邻域处理来锐化图像
变换域方法
将一幅图像变换到变换域中(如频域)，在变换域进行处理，然后通过反变换把处理结果返回到空间域。
2 灰度变换与空间滤波基础
空间域处理可由下式定义：
g(x,y)=T [ f(x,y) ]
f(x,y) — 输入图像
g(x,y) — 处理后图像
T — 在点(x,y)的邻域上定义的关于 f 的一种算子。
领域的定义：中心点在(x,y)的正方形子图像（如3x3邻域）
最小邻域的大小是1x1，即单个像素
这种情况下，g仅取决于输入图像f (x,y)在点(x,y)处的值；
此时T操作成为如下式的灰度变换函数：
s = T®
当我们使用r和s这两个符号时，其分别表示
f(x,y)和g(x,y)在任意点(对应位置)的灰度值；
这种结果取决于某一个点处的灰度的方法也称为点处理技术；
模板也叫（滤波器 核 掩模 窗口）
邻域中执行的操作类型决定了滤波处理的特性。
如：模板的系数决定了处理的性质是锐化，还是模糊。
3 基于灰度变换的图像增强
基本灰度变换函数
关键在于设计合适的映射函数（曲线）
映射设计的两类方法：
**灰度变换：**根据图像特点和处理工作需求，人为设计映射函数，试探处理效果。
**直方图修正：**从改变图像整体的灰度分布出发，设计一种映射函数。
图像反转
s=L-1-r；
这种处理得到的图像，与原图视觉内容相同。
适用于增强嵌入于图像暗色区域的白色或灰色细节，特别是当黑色面积占主导地位时。
对数变换
s= c⋅ log(1+r ) c 为常数，并假设r ≥ 0
其特点：
对数变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值，同时，对输入中范围较宽的高灰度值映射为输出中较窄范围的灰度值
作用：一般用于扩展图像的低灰度范围，同时压缩高灰度范围，使得图像灰度均匀分布。
重要特征：可以压缩像素值变化较大的图像的动态范围。
特点：对数变换与人类视觉特性相匹配。
幂律(伽马)变换
当c=r=1 时，将简化为正比变换。
用于扩展灰度级；在磁共振(MRI)图像中的应用
用于图像获取、打印和显示的各种设备是根据幂律来产生响应，校正这种幂律响应现象的处理称为伽马校正，
精确再现彩色图像，也需要伽马校正，因为改变伽马值不仅改变亮度，而且会改变彩色图像中的红绿蓝三色的比率；
幂律变换也可以用于扩展灰度级
可与对数变换配合使用构成复合滤波操作
随着伽马值从0.6减小到0.4，更多的细节变得可见，当减小到0.3时，背景中的细节得到进一步的增强，但对比度下降到图像有轻微的“冲淡”的效果
要处理的图像有“冲淡”的效果，表明需要进行灰度级的压缩，可令伽马值大于1进行处理；
分段线性变换函数
对比度拉伸
提高图像灰度级的动态范围。
灰度级分层
灰度级分层可用于突出特定灰度范围的亮度，可用于增强特征，主要包括两种基本方法：
1.将感兴趣范围内的所有灰度值显示为一个值（比如白色），而将其他灰度值显示为另一个值（比如黑色），该变换产生一个二值图像；
2.使感兴趣范围的灰度变亮（或变暗），而保持图像中其他灰度级不变。
直方图处理
横轴表示灰度级，纵轴表示图像中改灰度级出现的个数。
灰度直方图的性质：位置缺失性、一对多特性、可叠加性
直方图分布对图片的影响。
直方图分布较窄的图像，对比度低，图像看起来不清晰。
偏暗的图像，其直方图成分集中于左边一侧，即灰度值较小的一边
偏亮的图像，其直方图成分集中于右边一侧，即灰度值较大的一边。
直方图均匀分布时，图像灰度级丰富，且动态范围大，此时图像最清晰，
直方图均衡化
作用：图像的灰度趋向均匀，图像所占有的像素灰度间距拉开。直观体验是提高了图像对比度，改善视觉效果。
连续函数均衡化;
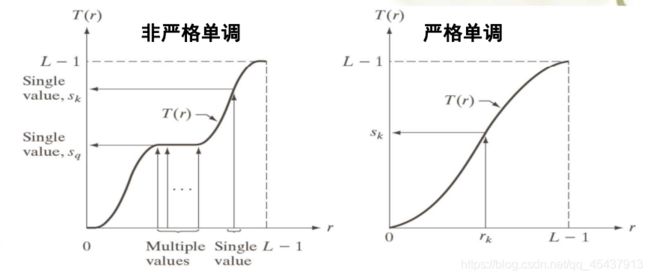
条件(a)保证通过灰度变换，原始图像的每个灰度级r都会产生一个灰度级s，且灰度变换前后不倒置；
条件(b)保证输出灰度级与输入有同样的范围。
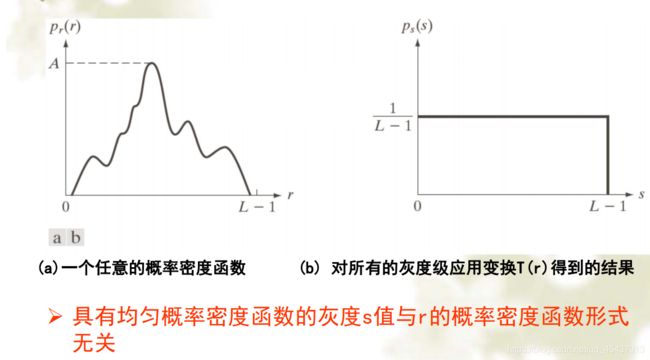
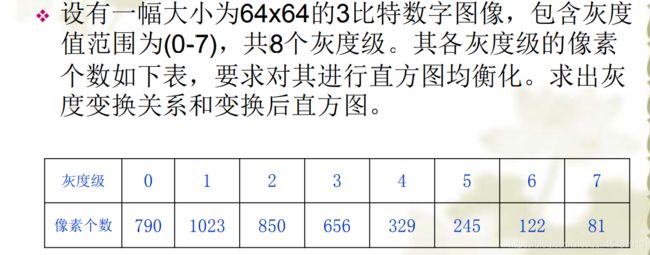
离散函数的均衡化
***计算的过程：
- 列出原始图像和变换后图像的灰度级L。
- 统计原始图像的直方图。
- 计算原始图像的累积直方图 。
- 根据计算得到的累积分布函数，建立输入图像与输出图像灰度级之间的对应关系。
- 根据对应关系得到变换后图像
- 计算变换后图像的直方图。***
直方图均衡化的特点：
能自动增强图像的对比度。
得到了全局均衡化的直方图，即均匀分布
效果不易控制
该处理完全是自动的，仅涉及到累积直方图的计算，可直接从已知图像提取的信息为基础，不需要更多的参数说明
直方 图规定化
一种用于产生具有特殊直方图分布的图像的方法，叫做直方图匹配或直方图规定化方法。
一般来说正确的选择规定化的函数有可能获得比直方图均衡化更好的效果。
对原图像与期望图像都做一次直方图均衡化
**直方图均衡化是直方图规定化的一种特例
直方图规定化的实现方法：
- 对原图像进行直方图均衡化，得到其累积直方图Pi ;
- 对规定直方图进行均衡化，得到其累积直方图Pj ;
- 按照Pj →Pi 最靠近的原则进行i→j的变换。
- 求出i→j的变换函数，对原图像进行灰度变换。**
直方图均衡化和直方图匹配的比较：
直方图均衡化：是增强该图像的一个好办法，以便使暗区 域的细节更清楚。输出的结果是具有明亮的“冲淡”外观的图像
直方图匹配：原始直方图的细小改变也会使图像的外观改变明显
局部直方图处理
4 基于空间滤波的图像增强
空间滤波基础
空间滤波：直接对图像像素进行处理。
空间滤波和频域滤波的联系和区别：
线性空间滤波与频域滤波之间存在着一一对应关系
但空间滤波可提供相当多的功能，还可以用于非线性滤波。这一点是频域滤波做不到的；
对于线性空间滤波器，其响应由滤波器系数与滤波掩模扫过区域的相应像素值的乘积之和给出。
如果没给出掩模大小就要使用m=2a+1，n=2b+1来自己设计掩模。
非线性空间滤波也基于邻域处理。不能直接用前述的乘积求和公式中的系数
平滑空间滤波器（均值滤波器）
目的：
用于模糊处理和减小噪声。
应用：
模糊处理经常用于预处理，如在提取大的目标之前去除图像的一些琐碎细节、桥接直线或曲线的缝隙；
平滑由灰度级数量不足引起的伪轮廓效应。
分类：
线性滤波
非线性滤波
平滑滤波器的输出是：待处理图像在滤波器掩模邻域内的像素的简单平均值。
属于低通滤波器
主要应用于去除图像中的不相干细节，这里“不相干”指的是与滤波掩模尺寸相比，较小的像素区域。
优点：减小了图像灰度的“尖锐”变化，常用于图像降噪。典型的随机噪声由灰度级的尖锐变化组成。
缺点：模糊了图像的边缘，因为边缘也是有图像灰度的尖锐变化造成的。
随着掩模尺寸的变大，模糊程度加大
空间均值处理的重要应用是，为了对感兴的物体得到一个粗略的描述而模糊一幅图像
掩模的大小由哪些即将融入背景的物体尺寸来决定。
应用：去除椒盐噪声。
锐化空间滤波器
二阶导数会在斜坡开始结束处产生双线现象。
使用二阶微分图像锐化——拉普拉斯算子
任意阶的微分都是线性操作，所以拉普拉斯变换也是线性操作。 最简单的各向同性的微分算子。
使用一节微分图像锐化——梯度法
拉普拉斯操作在增强细节方面有利，但会导致更多的噪声。梯度变换在灰度变换区域的响应更强烈，但其对噪声和小细节的响应相对拉普拉斯操作要弱一些；
可将梯度图像平滑处理，并用拉普拉斯图像相乘，乘积会保留灰度变化强烈区域的细节，同时减低灰度变化相对平坦区域的噪声，这种操作课粗略的看做是结合拉普拉斯操作与梯度操作的优点。