控制图简明原理及Plotly实现控制图Python实践

1. 控制图简明原理

1.1. 关于控制图概述

控制图（Control Chart）又叫管制图，图上有三条平行于横轴的直线：中心线（CL，Central Line）、上控制限（UCL，Upper Control Limit）和下控制限（LCL，Lower Control Limit），并有按时间顺序抽取的样本统计量数值的描点序列。UCL、CL、LCL统称为控制限

关于控制图的形成是通过把正态分布图旋转，就得到如下所示的控制图。

控制图是用于分析和判断过程是否处于稳定状态所使用的带有控制界限的图，是具有区分正常波动和异常波动的功能图表，是现场质量管理中重要的统计工具。 常规控制图包括计量值控制图 （包括单值控制图、平均数和极差控制图、中位数和极差控制图） 和计数值控制图（包括不合格品数控制图、不合格品率控制图、缺陷数控制图、单位缺陷数控制图等）两类。

1.2. 控制限的计算

1.2.1. 基本计算

如果数据基于正态分布，$X(\mu ,{\sigma }^2)$的前提，则控制界限为：$\mu \pm 3\sigma$，这个控制界限基于过程。

• $UCL=\mu +3\sigma$
• $CL=\mu$
• $LCL=\mu －3\sigma$

其中，$\mu$是均值，$\sigma$是标准差。

这里，所使用的均值和标准差是指所有数据，不是抽样的样本，样本的均值为$\bar{X}$，标准差表示为$s$。

1.2.2. SPC工程计算

工程上常见根据控制图类型，通过基于查表发计算获取控制限，详见GB∕T 17989.2-2020 常规控制图，国家标准。

SPC：
统计过程控制（Statistical Process Control）是一种借助数理统计方法的过程控制工具。它对生产过程进行分析评价，根据反馈信息及时发现系统性因素出现的征兆，并采取措施消除其影响，使过程维持在仅受随机性因素影响的受控状态，以达到控制质量的目的。

1.3. 控制图分类

控制图在众多现代化工厂中得到了普遍应用，并凭借其强大的分析功能，为工厂带来丰厚的实时收益。最初的控制图分为计量型与计数型两大类，包含七种基本图表。

计量型控制图包括：

• IX-MR（单值移动极差图）
• Xbar-R（均值极差图）
• Xbar-s（均值标准差图）

I-MR 控制图 Individual and Moving Range Charts
当数据作为单个观测值收集时，将无法计算每个子组的标准差。移动极差作为一种替代方式，通过计算两个或多个连续观测值的极差来计算过程变异（一组抽样n个数据中，最大值与最小值的差值）。
Xbar-R均值极差控制图
用于控制对象为长度、重量、强度、纯度、时间、收率和生产量等计量值的场合。Xbar控制图主要用于观察正态分布的均值的变化，R控制图主要用于观察正态分布分散或变异情况的变化，而Xbar-R控制图则将二者联合运用，用于观察正态分布的变化。
Xbar-s均值标准差控制图
与Xbar-R图相似，只是用标准差（s）图代替极差（R）图而已。
Xbar-s或Xbar-R控制图
多用于对每一个产品都进行检验，并且每一次有多次检验的情况，采用自动化检查和测量的场合。

计数型控制图包括：

• P（用于可变样本量的不合格品率）
• Np（用于固定样本量的不合格品数）
• u（用于可变样本量的单位缺陷数）
• c（用于固定样本量的缺陷数）

而随着科技的发展，控制图的种类也不断丰富。目前，已有数百种控制图可供企业选择。只需根据企业实际情况选择合适的控制图，您的企业就可以完美、精确地对生产过程进行分析。

关于极差计算，国标中B.24样子，为时间序列值间的差分计算。

1.4. 如何选择一个控制图

SPC（Statistical Process Control）统计过程控制，是六西格玛工业管理理论的其中一个重要模块。SPC 的控制图（control chart）是数据可视化的一个重要手段。而控制图的选择应该根据实际需求来，这里用决策树简单介绍选择控制图的原则，不作展开。

1.5. 关于控制图使用简述

1.5.1. 使用控制图视角定义控制图

控制图是旨在判别过程是否处于稳定状态，并通过改进过程获得更佳的稳定状态。

1.5.2. 国标中关于SPC过程异常判断准则8条

• 准则1：1个点子落在A区以外（点子越出控制界限）
• 准则2：连续9点落在中心线同一侧
• 准则3：连续6点递增或递减
• 准则4：连续14点中相邻点子总是上下交替
• 准则5：连续3点中有2点落在中心线同一侧B区以外
• 准则6：连续5点中有4点子落在中心线同一侧C区以外
• 准则7：连续15点落在中心线同两侧C区之内
• 准则8：连续8点落在中心线两侧且无1点在C区中
  

八种可查明原因的检验模式——《GB/T 17989.2-2020 控制图 第2部分：常规控制图》

2. Plotly实现控制图

2.1. 关于Plotly

Plotly是另一个免费进行数据分析和绘制图表的python开源库，建立在d3.js上。 Plotly图可下载为SVG，EPS或PNG格式，并简单地导入到Illustrator或者Photoshop中。

https://plotly.com/python/

2.2. 绘制控制图

随意给定义一组数据，a列为x，b列为y，如下图所示：

import pandas as pd
import numpy as np
import plotly.express as px
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import plotly as py
import plotly.offline as py

df = pd.read_excel("control.xlsx") # 加载数据
y = df['b']
x = df['a']
mean = df['b'].mean()
std = df['b'].std()
# 定义期望值为4，标准差为1
mean = 4
std = 1

LCL_mean = mean - 3*std
UCL_mean =  mean + 3*std

# 画控制限
def hline_annotation_dict(text):
  return dict(font=dict(color="black",size=12), showarrow=False, text=text)

fig = go.Figure()
# 画路径
fig.add_trace(go.Scatter(x=x, y=y, line=dict(color='black', width=1)))
fig.add_hline(y=LCL_mean, line_color='red', annotation = hline_annotation_dict('LCL = {0:.2f}'.format(LCL_mean)), annotation_position = 'right')
fig.add_hline(y=UCL_mean, line_color='red', annotation = hline_annotation_dict('UCL = {0:.2f}'.format(UCL_mean)), annotation_position = 'right')
fig.add_hline(y=df_mean.mean(), line_color='green', annotation = hline_annotation_dict('mean = {0:.2f}'.format(df_mean.mean())), annotation_position = 'right')
fig.update_yaxes(title_text='Average(Weight)', dtick=0.5)

fig.update_xaxes(title_text = '控制图')
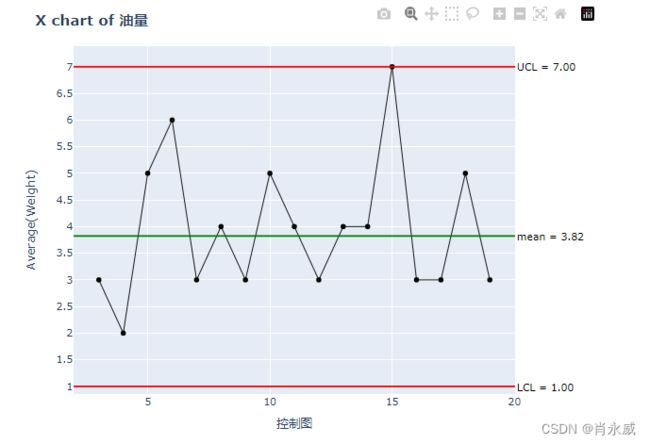
fig.update_layout(showlegend=False, title_text='X chart of 油量', margin=dict(t=50, r=100), width=700, height=540)

#py.plot(fig, filename='control chart')
fig.show()

输出控制图所示如下：

运行环境python3.8，plotly==5.11.0。

3. 其他

3.1. 常规控制图常数表

3.2. 适用场合

• 当你希望对过程输出的变化范围进行预测时；
• 当你判断一个过程是否稳定（处于统计受控状态）时；
• 当你分析过程变异来源是随机性还是非随机性时；
• 当你决定怎样完成一个质量改进项目时——防止特殊问题的出现，或对过程进行基础性的改变；
• 当你希望控制当前过程，问题出现时能觉察并对其采取补救措施时。

3.3. SPC控制图建立的步骤

• 选择质量特性
• 决定管制图之种类
• .决定样本大小,抽样频率和抽样方式
• 收集数据
• 计算管制参数(上,下管制界线等)
• 持续收集数据,利用管制图监视制程

3.4. 计数控制图的控制限计算公式

3.5. 本文的期望

使用控制图对量化分析结果的评价，例如一年12个月内油品销售波动情况描述，是不是平稳。
可以参考国标《GB∕T 17989.2-2020 控制图国家标准 第2部分:常规控制图》中“波动可查明原因的检验模式的注意事项”内容等。

参考：
肖永威. Python数据分析师使用低代码Streamlit实现Web数据可视化方法——Plotly可视化基础篇. CSDN博客. 2022.01
张宇. Python 实现 I-MR 控制图及 Plotly 可视化. 知乎. 2020.12
百度百科. 控制图
灰灰. Plotly实现12个常用的JMP图表. 知乎. 2021.10
GB∕T 17989.2-2020 控制图国家标准 第2部分:常规控制图