DIDL笔记(pytorch版)(六)
文章目录
- 前言
- 卷积运算和互相关运算
- 卷积之后输入输出大小问题
-
- 填充
- 步幅
- 通道问题
-
- 多输入通道
- 多输出通道
- 1 × \times × 1的卷积核
- 池化层
-
- 最大池化层和平均池化
- 填充和步幅
- 多通道
前言
只记录感兴趣的知识点。卷积是网络中的一个操作。
卷积运算和互相关运算
互相关运算就是输入子数组与核数组按照元素相乘并且求和得到。
但是卷积运算其实是数学中比较重要的运算,是一种特殊的加权求和。卷积运算与互相关运算的不同体现在"卷",意思是核数组需要在原来的基础上翻折或者旋转(180度)再和输入按位相乘并求和。
但其实没有关系,在深度学习领域里面,我们一般把互相关运算就叫做卷积运算,因为核数组旋转与否不影响最终结果。
参考:
https://zhuanlan.zhihu.com/p/345681510#:~:text=卷积,又称褶积,,微繁琐复杂一些%E3%80%82
https://www.zhihu.com/question/339496491
卷积之后输入输出大小问题
填充
n − 输 入 尺 寸 ; k − 卷 积 核 尺 寸 ; p − 填 充 行 ( 列 ) 数 n-输入尺寸;k-卷积核尺寸;p-填充行(列)数 n−输入尺寸;k−卷积核尺寸;p−填充行(列)数
非填充输出:![]()
填充输出:![]()
通常,为了保证输入输出大小一致设置: p = k − 1 p=k-1 p=k−1。当然填充肯定是均匀的填充的,如果k为奇数,设置 ( k − 1 ) / 2 (k-1)/2 (k−1)/2行(列)分别填充数据矩阵左右;如果k为偶数,可以设置顶(左)端添加 ⌈ ( k − 1 ) / 2 ⌉ \lceil(k-1)/2 \rceil ⌈(k−1)/2⌉行(列),设置 ⌊ ( k − 1 ) / 2 ⌋ \lfloor(k-1)/2 \rfloor ⌊(k−1)/2⌋行(列)填充数据矩阵底(右)端。因为偶数减一不好处理,所以我们经常看到是3,5,7大小的核。
而且这边的描述 p p p与代码的padding有所不同,padding=1意味着 p = 2 p=2 p=2,我个人的理解就是padding代表数据矩阵外围再包上一圈数据。
步幅
简单来说,就是核数组在输入数组上滑动时,需要动几格进行下一次运算。
填充步幅输出:

在实际设计网络时,一般会让输入的高和宽能分别被高和宽上的步幅整除。
通道问题
实际真实的数据可能是多通道的,比如彩色图像就是RGB三通道。多通道个人简单理解,就是一个图片由多个相关的数据矩阵组成。
多输入通道
一张彩色图片是有3个通道,也就是三个相关的数据矩阵。做卷积需要与矩阵做互相关运算。请记住:图有多少输入通道,一个卷积核就有多少通道。
输入通道与卷积核通道,一一对应做完互相关运算之后,得到的多个矩阵最后再把相同位置的加起来,形成一个特征图。所以如果不指定有多少输出通道,那么最后得到的特征图结果都为1通道。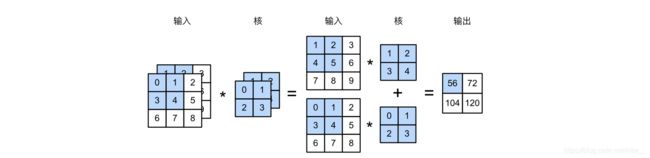
多输出通道
想要多通道输出,那么我们就需要多设置几个卷积核。请记住:希望有多少输出通道,卷积核就有多少个。
举个例子:一张3(通道) × \times ×h × \times ×w的输入与n × \times × 3 × \times ×k × \times ×k的卷积核做卷积,最后形成n × \times ×h × \times ×w的输出。(假设设置填充步幅使输入输出尺寸一致)
1 × \times × 1的卷积核
1 × \times × 1的卷积核没有再扩大感受野,只是通道之间是数据加了起来。
VGG中它主要用于增加网络的非线性,因为卷积之后跟上ReLU激活函数,它在没有改感受野的情况下就至0了一些元素保留其他元素。而且增加的网络的深度提高网络性能。
假设将通道维当作特征维,将高和宽维度上的元素当成数据样本,那么1×1卷积层的作用与全连接层等价。例如下图,有9个样本,每个样本是个3维的特征向量。(回头看看3.1.2更好理解)

# 等价演示代码
import torch
import d2l as d2l
def corr2d_multi_in(X, K):
# 沿着X和K的第0维(通道维)分别计算再相加
res = d2l.corr2d(X[0, :, :], K[0, :, :])
for i in range(1, X.shape[0]):
res += d2l.corr2d(X[i, :, :], K[i, :, :])
return res
def corr2d_multi_in_out(X, K):
# 对K的第0维遍历,每次同输入X做互相关计算。所有结果使用stack函数合并在一起
return torch.stack([corr2d_multi_in(X, k) for k in K])
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.view(c_i, h * w)
K = K.view(c_o, c_i)
Y = torch.mm(K, X) # 全连接层的矩阵乘法
return Y.view(c_o, h, w) # 数据形状调整
X = torch.rand(3, 3, 3)
K = torch.rand(2, 3, 1, 1)
Y1 = corr2d_multi_in_out_1x1(X, K) # 全连接层
Y2 = corr2d_multi_in_out(X, K) # 卷积层
print((Y1 - Y2).norm().item() < 1e-6)
池化层
卷积可以精准的找到像素变化的位置,但是我们不希望它对位置过度敏感。因为也许图像会有小小的改的,比如目标物体轻微的移动了位置,卷积可以精准的找出来,但其实会影响之后的识别,我们不需要这样的精准。
池化层缓解卷积层对位置的过度敏感。
池化层的作用:
- 特征不变性(feature invariant)
使模型更关注是否存在某些特征而不是特征具体的位置。可看作是一种很强的先验,使特征学习包含某种程度自由度,能容忍一些特征微小的位移。 - 特征降维。
- 在一定程度上能防止过拟合的发生。
参考:https://zhuanlan.zhihu.com/p/103350961
最大池化层和平均池化
填充和步幅
池化层和卷积层一样有填充和步幅,而且机制也一样。
多通道
在处理多通道输入数据时,池化层对每个输入通道分别池化,而不是像卷积层那样将各通道的输入按通道相加。这意味着池化层的输出通道数与输入通道数相等。
