《金融数据分析导论:基于R语言》习题答案(第一章)
《金融数据分析导论:基于R语言》是芝加哥大学的教授Ruey S.Tsay所著,李洪成、尚秀芬、郝瑞丽翻译,机械工业出版社出版,是一本学习R语言和金融数据分析的很好的参考书籍。
注:这些答案都是本人自己做出的结果,可能有错,仅供参考,发现有错的地方欢迎大家指出。
第一章
1.
首先,将数据包放在当前工作目录下
library(fBasics)
da = read.table("d-axp3dx-0111.txt",header=T) %读出数据
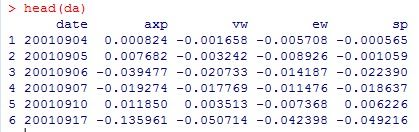
head(da) %显示数据的前6行,可以观察数据格式
mmm = da[,2:5] %取出简单收益率的数据,即把日期去掉
basicStats(mmm)
对mmm中的数据做基础分析,就可得到各列简单收益率序列的样本均值(Mean)、标准差(Stdev)、偏度(Skewness)、超额峰度(Kurtosis)、最大值(Maximum)、最小值(Minimum)
rs = log(mmm+1) %根据简单收益率求出对数收益率,公式为r=In(R+1)
basicStats(rs) %基础分析求出一系列统计值
ss = rs[,1]%取出AXP股票的对数收益率
t.test(ss)
p值大于0.05,接受原假设,即AXP对数收益率的均值为0
2.
首先,将数据包放在当前工作目录下
library(fBasics)
da = read.table("m-ge3dx-4011.txt",header=T) %读出数据
head(da) %显示数据的前6行,可以观察数据格式
mmm = da[,2:5] %取出简单收益率的数据,即把日期去掉
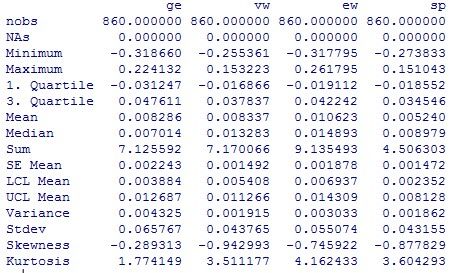
basicStats(mmm)
提示错误如下:
经检查发现在数据的第58行(不包括标题)19441031的sp数据为”.”(非数值数据),因此系统报错。通过上网查阅资料,只查到如何删除含有”NA”的行数据:na.omit(mmm)或mmm[complete.cases(mmm), ] [1],所以手工删除第58行:
mmm = mmm[-58,]%x = x[-m,]表示删除x矩阵中的第m行
然而删除了还是报同样的错误,于是我手工去txt文件里删除了第58行,就ok了,不知道程序怎么改才可以= =
然后继续
对mmm中的数据做基础分析,就可得到各列简单收益率序列的样本均值(Mean)、标准差(Stdev)、偏度(Skewness)、超额峰度(Kurtosis)、最大值(Maximum)、最小值(Minimum)
rs = log(mmm+1) %根据简单收益率求出对数收益率,公式为r=In(R+1)
basicStats(rs) %基础分析求出一系列统计值
ss = rs[,1]%取出AXP股票的对数收益率
t.test(ss)
p值小于0.05,拒绝原假设,即AXP对数收益率的均值不为0
3.
首先,将数据包放在当前工作目录下
library(fBasics)
da = read.table("m-ge3dx-4011.txt",header=T) %读出数据
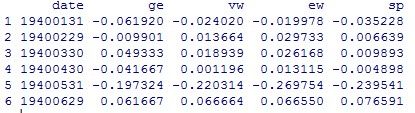
head(da) %显示数据的前6行,可以观察数据格式
mmm = da[,5] %取出S&P月收益率的数据
t.test(mmm) %做t检验
因为p值为2.436e-05<0.05,拒绝原假设,即S&P综合指数的月股票收益率均值不为0.
s3 = skewness(mmm)
T = length(mmm)
t3= s3/sqrt(6/T)
t3
t3为-7.057059,绝对值大于1.96,故拒绝原假设,即S&P综合指数的月股票收益率偏度不为0.
s4 = kurtosis(mmm) %计算出超额峰度
t4 = s4/sqrt(24/T)
t4
t4>1.96,故拒绝原假设,即S&P综合指数的月股票收益率的峰度不为3.
4.
首先,将数据包放在当前工作目录下
library(fBasics)
da = read.table("d-axp3dx-0111.txt",header=T) %读出数据
head(da) %显示数据的前6行,可以观察数据格式
mmm = da[,2] %取出第2列axp的日简单收益率的数据
rs = log(mmm+1) %求出对数收益率
s3 = skewness(rs)
T = length(rs)
t3= s3/sqrt(6/T)
t3
t3的绝对值小于1.96,故接受原假设,即axp日对数收益率的偏度度量等于0.
s4 = kurtosis(rs) %计算出超额峰度
t4 = s4/sqrt(24/T)
t4
t4>1.96,故拒绝原假设,即axp日对数收益率的月股票收益率的超额峰度不为0.
5.
首先,将数据包放在当前工作目录下
library(fBasics)
da = read.table("d-fx-ukus-0711.txt",header=T) %读出英镑对美元汇率数据
head(da) %显示数据的前6行,可以观察数据格式
发现最后一列是英镑对美元的汇率,取出最后一列数
mmm = da[,4]
将其转换为美元兑英镑的汇率
mmm = 1/mmm
根据每天的汇率值求出每天的日对数收益率,rt = In(pt/p(t-1)),rt是第t期的日对数收益率,pt是第t期的汇率值,设第1期r1 = In(pt/p(t-1)) = In1 = 0,循环计算从第2期到第length(mmm)期的日对数收益率。
r1 = 1:length(mmm) %定义一个数组表示日对数收益率
r1[1] = 0 %设定第1天的日对数收益率为0
for (i in 2:length(r1)) {
r1[i]=log(mmm[i]/mmm[i-1])
}
r1即为美元对英镑的汇率从20070102-20111130的日对数收益率。
同样的办法求出美元对日元的汇率从20070102-20111130的日对数收益率。
da = read.table("d-fx-usjp-0711.txt",header=T)
head(da)
r2= 1:length(mmm)
r2[1] = 0
for (i in 2:length(r2)) {
r2[i]=log(mmm[i]/mmm[i-1])
}
r2即为美元对日元的汇率从20070102-20111130的日对数收益率。
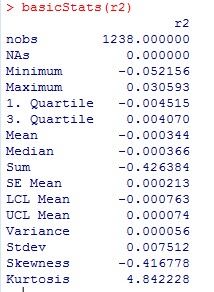
对r1和r2分别作基础分析,即可得到它们的样本均值(Mean)、标准差(Stdev)、偏度(Skewness)、超额峰度(Kurtosis)、最大值(Maximum)和最小值(Minimum)。
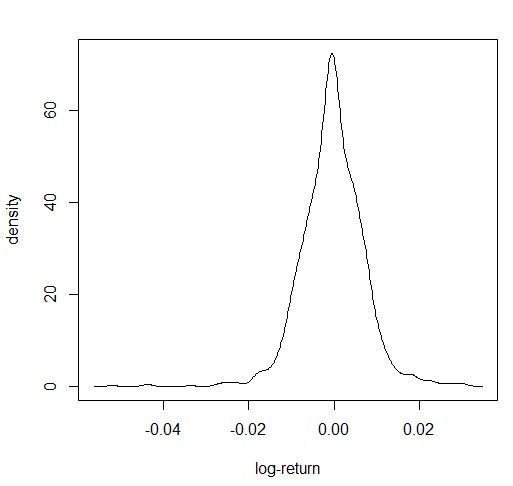
对于数据集r2,求其密度分布的公式是d = density(r2),画图函数为plot(d$x, d$y, xlab=’log-return’, ylab=’density’, type=’l’)(这两个公式见书中第35页的代码)
d = density(r2)
plot(d$x,d$y,xlab='log-return',ylab='density',type='l')
得到密度图如下:
假设检验(t检验):
t.test(r2)
p值大于0.05,接受原假设,即美元/日元汇率的日对数收益率的均值为0.
[1]人大经济论坛http://bbs.pinggu.org/thread-2331183-1-1.html
吐槽:R的矩阵定义好复杂啊