阵列信号处理仿真二——波束方向图的绘制
均匀加权线阵的频率响应和波束方向图
-
- 导入
- 频率波束响应 Υ ( ψ ) \Upsilon(\psi) Υ(ψ)
- 波数方向图
- 波束方向图的幅值在不同方向上的对应关系
- 阵元间距对波束方向图的影响
- matlab的绘图代码
导入
假设存在一个均匀线阵,我们把阵列的中心放在了坐标系的原点,线阵共有N个阵元,接下来我们将介绍该线阵不同的性质及其对应的图形,介于下方用到的关系换算,我们现在这里声明一下
ψ = − k z d = 2 π λ c o s ( θ ) ⋅ d = 2 π λ u z d \psi = -k_zd = \frac{2\pi}{\lambda}cos(\theta)·d = \frac{2\pi}{\lambda}u_zd ψ=−kzd=λ2πcos(θ)⋅d=λ2πuzd
频率波束响应 Υ ( ψ ) \Upsilon(\psi) Υ(ψ)
Υ ψ ( ψ ) = 1 N s i n ( N ψ 2 ) s i n ( ψ 2 ) \Upsilon_\psi(\psi) = \frac{1}{N}\frac{sin(N\frac{\psi}{2})}{sin(\frac{\psi}{2})} Υψ(ψ)=N1sin(2ψ)sin(N2ψ)
对于普遍情况,频率波数响应函数的定义如下:
Υ ( ω , k ) = H T ( ω ) v k ( k ) \Upsilon(\omega,k) = H^T(\omega)v_k(k) Υ(ω,k)=HT(ω)vk(k)
其中 v k ( k ) v_k(k) vk(k)称为阵列流形矢量,包含了阵列所有的空间特征
v k ( k ) = [ e − j k T p 0 e − j k T p 1 ⋮ e − j k T p N − 1 ] v_k(k)= \begin{bmatrix} e^{-jk^Tp_0} \\ e^{-jk^Tp_1} \\ \vdots\\ e^{-jk^Tp_{N-1}}\\ \end{bmatrix} vk(k)=⎣ ⎡e−jkTp0e−jkTp1⋮e−jkTpN−1⎦ ⎤
对于窄带信号而言,具有以下特点
ω H = H T ( ω c ) \omega^H = H^T(\omega_c) ωH=HT(ωc)
现在我们关注均匀加权的情况
ω ( n ) = 1 N , n = 0 , 1 , 2 ⋯ N − 1. \omega(n) = \frac{1}{N},n=0,1,2\cdots N-1. ω(n)=N1,n=0,1,2⋯N−1.
我们可以把上式改写成
ω = 1 N 1 \omega = \frac{1}{N}1 ω=N11
通过上述的声明和对公式的化简之后,我们可以得到 ψ \psi ψ空间的频率—波数函数
Υ ψ ( ψ ) = 1 N e − j ( N − 1 2 ) ψ [ 1 − e j N ψ 1 − e ψ ] \Upsilon_\psi(\psi) = \frac{1}{N}e^{-j(\frac{N-1}{2})\psi}[\frac{1-e^{jN\psi}}{1-e^\psi}] Υψ(ψ)=N1e−j(2N−1)ψ[1−eψ1−ejNψ]
或者
Υ ψ ( ψ ) = 1 N s i n ( N ψ 2 ) s i n ( ψ 2 ) , − ∞ < ψ < ∞ \Upsilon_\psi(\psi) = \frac{1}{N}\frac{sin(N\frac{\psi}{2})}{sin(\frac{\psi}{2})},-\infty <\psi<\infty Υψ(ψ)=N1sin(2ψ)sin(N2ψ),−∞<ψ<∞
下面我们给出N = 11的频率波数响应图

Υ ( ψ ) : ψ = 2 π λ d c o s θ , N = 11 \Upsilon(\psi):\psi=\frac{2\pi}{\lambda}dcos\theta,N=11 Υ(ψ):ψ=λ2πdcosθ,N=11
用dB表示
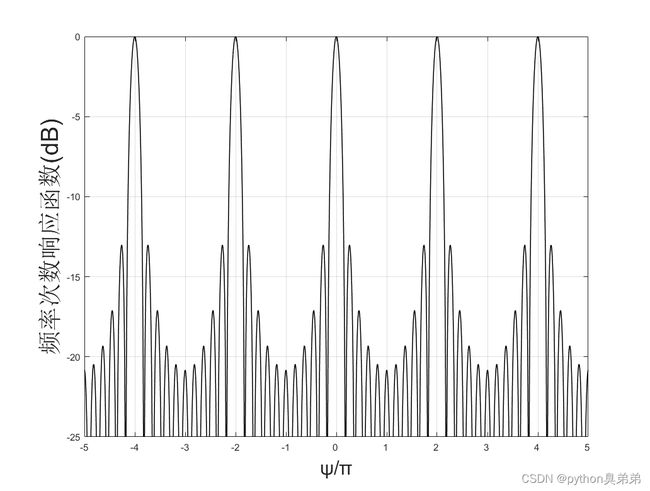
波数方向图
θ \theta θ 空间的波数方向图为
B θ ( θ ) = 1 N s i n ( N 2 ⋅ 2 π λ c o s θ ⋅ d ) s i n ( 1 2 ⋅ 2 π λ c o s θ ⋅ d ) , 0 ≤ θ ≤ π B_\theta(\theta) = \frac{1}{N}\frac{sin(\frac{N}{2}\cdot\frac{2\pi}{\lambda}cos\theta\cdot d)}{sin(\frac{1}{2}\cdot\frac{2\pi}{\lambda}cos\theta\cdot d)},0\le \theta \le \pi Bθ(θ)=N1sin(21⋅λ2πcosθ⋅d)sin(2N⋅λ2πcosθ⋅d),0≤θ≤π
在极坐标下画出 B θ ( θ ) B_\theta(\theta) Bθ(θ)

波束方向图的幅值在不同方向上的对应关系
k z k_z kz空间的函数如下
Υ ( ω : k z ) = 1 N s i n ( N k z d 2 ) s i n ( k z d 2 ) \Upsilon(\omega:k_z) = \frac{1}{N}\frac{sin(Nk_z\frac{d}{2})}{sin(k_z\frac{d}{2})} Υ(ω:kz)=N1sin(kz2d)sin(Nkz2d)
根据 Υ ( ψ ) \Upsilon(\psi) Υ(ψ)以及 ψ \psi ψ和其他变量的对应关系,可以的到不同空间的函数,对其取模即可的到幅值,各空间对应如下
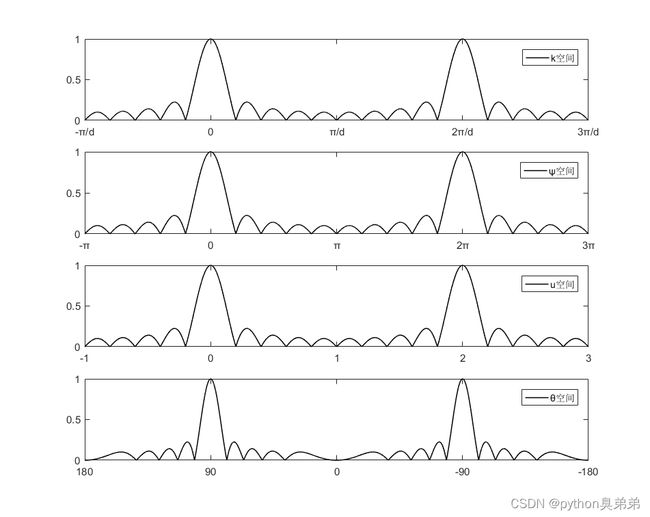
阵元间距对波束方向图的影响
u u u的可视区域及实际中的到的响应的范围在-1到1之间,下图展示了不同的d对波束方向图的影响

matlab的绘图代码
注意设置不同的坐标刻度和显示内容以达到预期效果
psi = -5*pi:0.001:5*pi;
N = 11;
Upsilon_psi= 1/N* sin(N*psi/2)./sin(psi/2);
figure(1)
set(gcf,'Position',[100,100,900,680])
plot(psi,Upsilon_psi,'LineWidth',1,'Color','k');
xlim([-5*pi,5*pi])
ylim([-0.4,1])
set(gca,'xTick',[-5*pi,-4*pi,-3*pi,-2*pi,-1*pi,0,pi,2*pi,3*pi,4*pi,5*pi]);
set(gca,'xticklabel',[-5,-4,-3,-2,-1,0,1,2,3,4,5]);
xlabel('ψ/π','FontSize',20)
ylabel('频率次数响应函数','FontSize',25)
grid on
Upsilon_dB_psi = 10*log10(abs(Upsilon_psi).^2);
figure(2)
set(gcf,'Position',[100,100,900,680])
plot(psi,Upsilon_dB_psi,'LineWidth',1,'Color','k');
xlim([-5*pi,5*pi])
ylim([-25,0])
set(gca,'xTick',[-5*pi,-4*pi,-3*pi,-2*pi,-1*pi,0,pi,2*pi,3*pi,4*pi,5*pi]);
set(gca,'xticklabel',[-5,-4,-3,-2,-1,0,1,2,3,4,5]);
xlabel('ψ/π','FontSize',20)
ylabel('频率次数响应函数(dB)','FontSize',25)
grid on
theta = -pi:0.000001:pi;
B_theta = 1/11*(sin(5.5*pi*cos(theta))./sin(0.5*pi*cos(theta)));
B_theta = 10*log10(abs(B_theta));
B_theta(B_theta<-35) = -35;
polarplot(theta,B_theta,'linewidth',1,'color','k')
pax = gca;
pax.ThetaZeroLocation = 'top';
pax.ThetaDir = 'clockwise';
thetalim([-180 180])
rlim([-35 0])
theta = -pi:0.001:pi;
psi = -pi:0.001:3*pi;
k = -pi:0.001:3*pi;
u = -1:0.001:3;
N = 10;
Upsilon_theta = 1/N*((sin(5*pi*cos(theta)))./sin(0.5*pi*cos(theta)));
Upsilon_psi = 1/N*((sin(5*psi))./(sin(0.5*psi)));
Upsilon_u_z = 1/N*((sin(5*pi*u))./sin(0.5*pi*u));
figure
set(gcf,'Position',[50,50,830,660])
subplot(4,1,4)
plot(theta,abs(Upsilon_theta),'LineWidth',1,'Color','k')
ylim([0,1])
xlim([-pi,pi])
set(gca, 'XTick', [-pi -pi/2 0 pi/2 pi])
set(gca,'xtickLabel',{180, 90, 0 -90 -180})
legend('θ空间')
subplot(4,1,1)
plot(psi,abs(Upsilon_psi),'LineWidth',1,'Color','k')
ylim([0,1])
xlim([-pi,3*pi])
set(gca, 'XTick', [-pi 0 pi 2*pi 3*pi])
set(gca,'xtickLabel',{'-π/d',0,'π/d','2π/d','3π/d'})
legend('k空间')
subplot(4,1,2)
plot(psi,abs(Upsilon_psi),'LineWidth',1,'Color','k')
ylim([0,1])
xlim([-pi,3*pi])
set(gca, 'XTick', [-pi 0 pi 2*pi 3*pi])
set(gca,'xtickLabel',{'-π',0,'π','2π','3π'})
legend('ψ空间')
subplot(4,1,3)
plot(u,abs(Upsilon_u_z),'LineWidth',1,'Color','k')
ylim([0,1])
xlim([-1 3])
set(gca, 'XTick', [-1 0 1 2 3])
legend('u空间')
u = -3:0.001:3;
N = 10;
Upsilon_u_z1 = 1/N*((sin(2.5*pi*u))./sin(0.25*pi*u));
Upsilon_u_z2 = 1/N*((sin(5*pi*u))./sin(0.5*pi*u));
Upsilon_u_z3 = 1/N*((sin(10*pi*u))./sin(pi*u));
Upsilon_dB_u1 = 10*log10(abs(Upsilon_u_z1).^2);
Upsilon_dB_u2 = 10*log10(abs(Upsilon_u_z2).^2);
Upsilon_dB_u3 = 10*log10(abs(Upsilon_u_z3).^2);
figure
set(gcf,'Position',[50,50,830,730])
subplot(3,1,1)
plot(u,Upsilon_dB_u1,'LineWidth',1,'Color','k')
ylim([-25,5])
xlim([-3,3])
set(gca, 'XTick', [-3 -2 -1 0 1 2 3])
legend('d=λ/4')
grid on
subplot(3,1,2)
plot(u,Upsilon_dB_u2,'LineWidth',1,'Color','k')
ylim([-25,5])
xlim([-3,3])
set(gca, 'XTick', [-3 -2 -1 0 1 2 3])
legend('d=λ/2')
grid on
subplot(3,1,3)
plot(u,Upsilon_dB_u3,'LineWidth',1,'Color','k')
ylim([-25,5])
xlim([-3,3])
set(gca, 'XTick', [-3 -2 -1 0 1 2 3])
legend('d=λ')
grid on
有关阵列的详细知识点可参考书目:最优阵列信号处理 汤俊译 清华大学出版社