滤波估计理论（一）——贝叶斯滤波

参考文献： Särkkä S. Bayesian filtering and smoothing[M]. Cambridge University Press, 2013.

从定义上来说，贝叶斯滤波是通过假设系统状态和观测都服从一定的概率分布，从而利用贝叶斯法则求解最优估计的问题的一类算法。这是因为在绝大部分问题中，我们都会假设我们需要估计的变量服从一定真值和噪声的分布。如果我们能估计出噪声的统计特征，从而将噪声去除，我们就可以得到真实的系统状态和观测量。为了更好的理解这里概念，我们先从一个常见问题的不同数学模型入手。

估计问题的建模

状态空间模型

假设我们现在有一个遥控小机器人，我们可以通过机器人上安装的GPS等跟踪设备获得机器人当前位置的量测信息，记为${\mathbf{z}}_k$；同时，我们根据遥控器输出的控制信息${\mathbf{u}}_k$和上一时刻机器人的位置，也可以估计出机器人当前位置的预测信息，记为${\mathbf{x}}_k$。用数学模型来描述上述两个量有：
$$\{\begin{array}{rl}& {\mathbf{x}}_k=f({\mathbf{x}}_{k-1},{\mathbf{u}}_k)+{\mathbf{w}}_k\\ & {\mathbf{z}}_k=h({\mathbf{x}}_k)+{\mathbf{v}}_k\end{array}\text{\hspace{1em}(1)}$$
该模型是一个典型的状态空间模型，上下两式分别成为状态空间的状态方程和量测方程。

概率模型

现在再让我们从概率的角度来重新思考上面的问题，由于跟踪设备获得的量测信息和我们根据控制信息得到的预测信息都不是完全准确的（否则也就没有进行估计的必要了），但其一定在真值附近的一定范围内，因此我们可以假设这两个信息服从一定的概率分布来表征二者在真值附近的不确定性。同时，我们现在可以拥有的信息包括前$k-1$时刻的预测和量测，因此$k$时刻的预测信息和量测信息本质上是一个条件概率模型：
$$\{\begin{array}{rl}& {\mathbf{x}}_k\sim p(x_k|x_{0:k-1},z_{1:k-1})\\ & {\mathbf{z}}_k\sim p(y_k|x_{0:k},z_{1:k-1})\end{array}\text{\hspace{1em}(2)}$$
上式与状态空间模型十分类似但又有所不同，这是因为上式是更为一般的估计模型，需要对其进行一定简化。最优状态估计的过程，其实是通过一组已知观测量反向估计出未知系统状态的过程，即概率反演过程。而这种状态量隐含且按照时序排列的模型称为隐马尔科夫模型（Hidden Markov Model，HMM）。

HMM模型

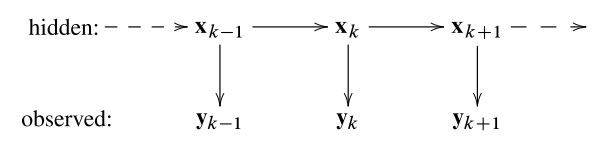
而HMM模型具有两个重要性质：
性质1：状态量具有马尔科夫性
在HMM模型中，状态${\mathbf{x}}_k$在给定前一时刻状态${\mathbf{x}}_{k-1}$的条件下和$k-1$之前的任意量测和状态均无关，同时和之后的状态以及量测也无关。
性质2：量测量具有条件独立性
在给定当前状态${\mathbf{x}}_k$的条件下，当前量测${\mathbf{z}}_k$和所有的历史状态以及量测均无关。

利用这两个性质，式(2)可以简化为：
$$\{\begin{array}{rl}& {\mathbf{x}}_k\sim p(x_k|x_{k-1})\\ & {\mathbf{z}}_k\sim p(z_k|x_k)\end{array}\text{\hspace{1em}(3)}$$
至此，我们得到了和之前的状态空间模型基本一致，但使用条件概率表示的模型，该模型称为概率状态空间模型。

贝叶斯估计方法

批处理贝叶斯估计

在建立了概率状态空间模型之后，我们可以得到全状态$\mathcal{X}=\{{\mathbf{x}}_0,\cdots ,{\mathbf{x}}_k\}$的联合先验分布$p({\mathbf{x}}_{0:k})$和所有量测量的似然$p({\mathbf{z}}_{0:k}|{\mathbf{x}}_{0:k})$为：
$$\{\begin{array}{rl}& {\mathbf{x}}_k\sim p(x_k|x_{k-1})\\ & {\mathbf{z}}_k\sim p(z_k|x_k)\end{array}\text{\hspace{1em}(4)}$$
因此对于$0\sim k$时刻的所有状态量和量测量，根据贝叶斯法则我们可以获得全状态的后验分布为：
$$p({\mathbf{x}}_{0:k}|{\mathbf{z}}_{1:k})=\frac{p({\mathbf{z}}_{1:k}|{\mathbf{x}}_{0:k})p({\mathbf{x}}_{0:k})}{p({\mathbf{z}}_{1:k})}\propto p({\mathbf{z}}_{1:k}|{\mathbf{x}}_{0:k})p({\mathbf{x}}_{0:k})\text{\hspace{1em}(5)}$$
对于全状态${\mathbf{x}}_{0:k}$来说，使得上述后验分布最大的值即为其最优估计。

预测，滤波还是平滑？

在进一步讨论贝叶斯滤波的相关问题之前，我们先来讨论一下几个状态估计领域常见三个名词：预测（prediction），滤波（filtering）和平滑（smoothing）。

批处理贝叶斯估计给出了全状态${\mathbf{x}}_{0:k}$的最大后验分布，但毫无疑问并非在所有的实际应用中我们都需要对所有的状态量和量测量进行同步估计，而是选择估计如下的边缘分布：

• 滤波分布(filtering distribution):在给定当前和之前量测信息${\mathbf{z}}_{1:k}$条件下，当前状态${\mathbf{x}}_k$的边缘分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})$。
• 预测分布(prediction distribution):在给定当前和之前量测信息${\mathbf{z}}_{1:k}$条件下，未来状态${\mathbf{x}}_{k+n}$的边缘分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})$。
• 平滑分布(smoothing distribution):在给定量测区间${\mathbf{z}}_{1:T}$的条件下，当前状态${\mathbf{x}}_k$的边缘分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:T})$，其中$T>k$。
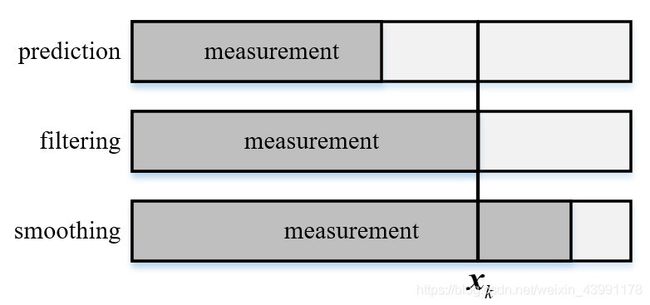
  预测、滤波与平滑

贝叶斯滤波

在明确了预测、滤波和平滑的概念之后，我们再回到贝叶斯估计中。贝叶斯滤波，本质上是一种递归贝叶斯估计，即通过贝叶斯估计计算滤波分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})$。

在推导贝叶斯滤波的具体公式之前，我们先整理一下手里已有的信息和需要求解的分布：

• 已知信息：上一时刻分布$p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})$和当前时刻量测$p({\mathbf{z}}_k|{\mathbf{x}}_k)$
• 位置信息：当前时刻分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})$

状态预测

假设现在我们尚未获得$k$时刻的量测量，只有$k-1$时刻对系统状态的预测$p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})$，那么此时我们可以获得其和$k$时刻的状态分布$p({\mathbf{x}}_k)$的联合概率分布$p({\mathbf{x}}_k,{\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})$为：
$$\begin{array}{rl}p({\mathbf{x}}_k,{\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})=& \frac{p({\mathbf{x}}_k,{\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1})}{p({\mathbf{z}}_{1:k-1})}\\ =& \frac{p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1})p({\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1})}{p({\mathbf{z}}_{1:k-1})}\\ =& \frac{p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1})p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})p({\mathbf{z}}_{1:k-1})}{p({\mathbf{z}}_{1:k-1})}\\ =& p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1})p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})\\ =& p({\mathbf{x}}_k|{\mathbf{x}}_{k-1})p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})\end{array}\text{\hspace{1em}(6)}$$
在最后一步化简中，我们利用了HMM的Markov性（${\mathbf{x}}_k$只和${\mathbf{x}}_{k-1}$相关）。将式（6）对${\mathbf{x}}_{k-1}$进行积分，即可得到${\mathbf{x}}_k$在只有量测${\mathbf{z}}_{1:k-1}$下的边缘条件概率：
$$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})=\int p({\mathbf{x}}_k|{\mathbf{x}}_{k-1})p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})d{\mathbf{x}}_{k-1}\text{\hspace{1em}(7)}$$
式（7）即表征了贝叶斯滤波中的一步预测过程，而其离散形式便是Markov链中经典的CK方程（Chapman-Kolmogorov Equation）。

量测更新

在完成对于状态的一步预测之后，此时我们有获取了$k$时刻的量测信息，那么我们很容易利用贝叶斯法则从已知分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})$和$p({\mathbf{z}}_k|{\mathbf{x}}_k)$求解条件分布$p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})$：
$$\begin{array}{r}p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})=\frac{p({\mathbf{x}}_k,{\mathbf{z}}_{1:k})}{p({\mathbf{z}}_{1:k})}\end{array}\text{\hspace{1em}(8)}$$
我们首先来看分子所表示的联合概率分布，根据概率链式法则有：
$$\begin{array}{rl}p({\mathbf{x}}_k,{\mathbf{z}}_{1:k})=& p({\mathbf{z}}_k|{\mathbf{x}}_k,{\mathbf{z}}_{1:k-1})p({\mathbf{x}}_k,{\mathbf{z}}_{1:k-1})\\ =& p({\mathbf{z}}_k|{\mathbf{x}}_k,{\mathbf{z}}_{1:k-1})p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})p({\mathbf{z}}_{1:k-1})\\ =& p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})p({\mathbf{z}}_{1:k-1})\end{array}\text{\hspace{1em}(9)}$$
其中第三部化简中利用了量测独立性$p({\mathbf{z}}_k|{\mathbf{x}}_k,{\mathbf{z}}_{1:k-1})=p({\mathbf{z}}_k|{\mathbf{x}}_k)$。 而对于分母$p({\mathbf{z}}_{1:k})$来说，虽然我们没有任何直接信息，但我们可以通过对上式所示的联合分布积分的方式来获取对应的边缘分布：
$$p({\mathbf{z}}_{1:k})=\int p({\mathbf{x}}_k,{\mathbf{z}}_{1:k})d{\mathbf{x}}_k=p({\mathbf{z}}_{1:k-1})\int p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})\text{\hspace{1em}(10)}$$
将式（9）和式（10）一起带入式（8）有：
$$\begin{array}{rl}p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})& =\frac{p({\mathbf{x}}_k,{\mathbf{z}}_{1:k})}{p({\mathbf{z}}_{1:k})}\\ & =\frac{p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})p({\mathbf{z}}_{1:k-1})}{p({\mathbf{z}}_{1:k-1})\int p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})}\\ & =\frac{p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})}{\underset{Z_k}{\int p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})}}\end{array}\text{\hspace{1em}(11)}$$
式（11）即为贝叶斯滤波的量测更新公式，式中$Z_k$称为归一化常数。

总结

至此，我们推导出了一个具有如式（12）所示的递推贝叶斯估计——贝叶斯滤波，贝叶斯滤波的每次估计都由状态预测和量测更新两步组成，循环往复，周而复始。
$$\{\begin{array}{rl}& p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})=\int p({\mathbf{x}}_k|{\mathbf{x}}_{k-1})p({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1})d{\mathbf{x}}_{k-1}\\ & p({\mathbf{x}}_k|{\mathbf{z}}_{1:k})=\frac{p({\mathbf{z}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1})}{Z_k}\end{array}\text{\hspace{1em}(12)}$$
虽然贝叶斯滤波从形式上看非常的简单易懂，但其各项分布的选取和积分的计算仍然不是一个简单的问题，需要根据不同的应用环境做不同的假设。而在不同假设下诞生了KF、EKF、UKF等广为人知的滤波方法，在后续章节中，我们将进一步从贝叶斯估计出发，逐一推导这些经典滤波方法。