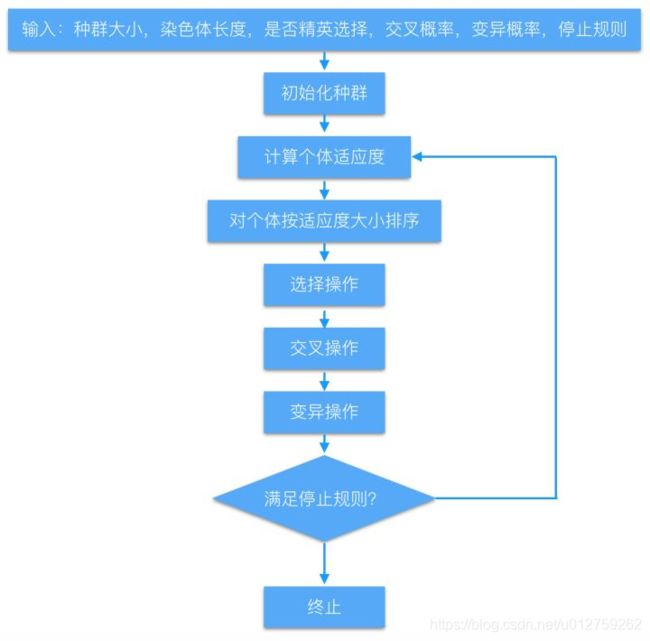
遗传算法
0. 研究问题
在区间[-4,4]的这个区间内找6个数,使得 f ( x ) = ∑ i = 1 6 w i x i f(x) = \sum_{i=1}^{6}w_ix_i f(x)=∑i=16wixi最大 。
事实上,不管一个函数的形状多么奇怪,遗传算法都能在很短的时间内找到它在一个区间内的(近似)最大值。
1. 介绍
遗传算法(Genetic Algorithm)遵循『适者生存』、『优胜劣汰』的原则,是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
主要步骤:
- 选择(Selection)
- 交叉(Crossover)
- 变异(Mutation)
2. 基本概念与名词解释
-
编码 -> 创造染色体
-
个体 -> 种群
-
适应度函数
-
遗传算子
- 选择
- 交叉
- 变异
-
运行参数
- 是否选择精英操作
- 种群大小
- 染色体长度
- 最大迭代次数
- 交叉概率
- 变异概率
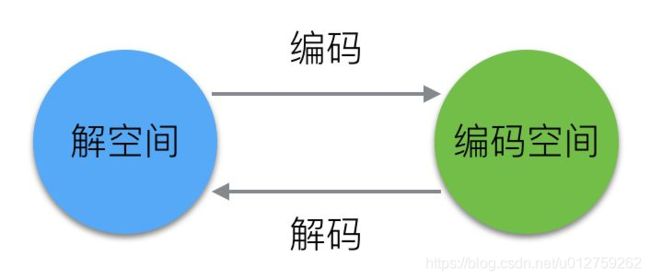
2.1 编码与解码
实现遗传算法的第一步就是明确对求解问题的编码和解码方式。一般来说,有两种编码方式:
- 实数编码:直接用实数表示基因,容易理解且不需要解码过程,但容易过早收敛,从而陷入局部最优。
- 二进制编码:稳定性高,种群多样性大,但需要的存储空间大,需要解码且难以理解。
哈哈哈,所以一般来说,大家选用的都是二进制编码喽?
目标函数: f ( x ) = x + 10 ∗ s i n ( 5 ∗ x ) + 7 ∗ c o s ( 4 ∗ x ) , x ∈ [ 0 , 9 ] f(x) = x + 10*sin(5*x) + 7*cos(4*x), x∈[0,9] f(x)=x+10∗sin(5∗x)+7∗cos(4∗x),x∈[0,9]
1. 编码方式:确定表示解所需要的染色体位数。
假如设定求解的精度为小数点后4位,可以将x的解空间划分为 (9-0)×(1e+4)=90000个等分。
这里作者这么划分的原因是:每一个等分代表小数点的一位,故而有90000个等分。
要表示这些串: 2 16 < 90000 < 2 17 2^{16}<90000<2^{17} 216<90000<217,需要17位二进制数来表示这些解。换句话说,一个解的编码就是一个17位的二进制串。
这个17位的二进制串就称为:染色体。
2. 解码方式
解码方式所需要的公式为:
f(x), x∈[lower_bound, upper_bound]
x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)
- lower_bound: 函数定义域的下限
- upper_bound: 函数定义域的上限
- chromosome_size: 染色体的长度
则在本例中,解码方式为:
x = 0 + d e c i m a l ( c h r o m o s o m e ) × ( 9 − 0 ) / ( 2 17 − 1 ) x = 0 + decimal(chromosome)×(9-0)/(2^{17}-1) x=0+decimal(chromosome)×(9−0)/(217−1)
decimal( ): 将二进制数转化为十进制数
2.2 个体与种群
『个体』:『染色体』表达了某种特征,这种特征的载体,称为『个体』。
『种群』:『个体』的集合。
Question: 染色体不是代表解吗?个体是啥玩意?
在本章中,个体就是目标函数的解,这个函数的所有解就称为种群。我们的目标就是要找到一个最佳的个体。
2.3 适应度函数
遗传算法中,一个个体(解)的好坏用适应度函数值来评价,在本问题中,f(x)就是适应度函数。
适应度函数值越大,解的质量越高。
适应度函数是遗传算法进化的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。
2.4 遗传算子
希望有这样一个种群,它所包含的个体所对应的函数值都很接近于 f ( x ) f(x) f(x)在 [ 0 , 9 ] [0,9] [0,9]上的最大值。
Question: 我曹?从找最优的个体变成了找种群?
如何让种群变得优秀呢?
不断的进化。
每一次进化都尽可能保留种群中的优秀个体,淘汰掉不理想的个体,并且在优秀个体之间进行染色体交叉,有些个体还可能出现变异。
种群的每一次进化,都会产生一个最优个体。种群所有世代的最优个体,可能就是函数f(x)最大值对应的定义域中的点。
如果种群无休止地进化,那总能找到最好的解。但实际上,我们的时间有限,通常在得到一个看上去不错的解时,便终止了进化。
Question: 保留最优的进化个体,你有啥办法保证它不退化呢?
2.5 进化方法
2.5.1 基本流程
-
选择(selection):
- 从前代种群中选择多对较优个体,一对较优个体称之为一对父母,让父母们将它们的基因传递到下一代,直到下一代个体数量达到种群数量上限。
- 在选择操作前,将种群中个体按照适应度从小到大进行排列(按照评估方法从小到大排列)
- 采用轮盘赌选择方法(当然还有很多别的选择方法),各个个体被选中的概率与其适应度函数值大小成正比。轮盘赌选择方法具有随机性,在选择的过程中可能会丢掉较好的个体,所以可以使用精英机制,将前代最优个体直接选择。
-
交叉(crossover):
- 两个待交叉的不同的染色体(父母)根据**交叉概率(cross_rate)**按某种方式交换其部分基因
- 采用单点交叉法,也可以使用其他交叉方法
-
变异(mutation)
- 染色体按照变异概率(mutate_rate)进行染色体的变异
- 采用单点变异法,也可以使用其他变异方法
-
复制
- 每次进化中,为了保留上一代优良的染色体,需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。
假设每次进化都需生成N条染色体,那么每次进化中,通过交叉方式需要生成N-M条染色体,剩余的M条染色体通过复制上一代适应度最高的M条染色体而来。
交叉概率(cross_rate)比较大,变异概率(mutate_rate)极低。像求解函数最大值这类问题,我设置的交叉概率(cross_rate)是0.6,变异概率(mutate_rate)是0.01。
因为遗传算法相信2条优秀的父母染色体交叉更有可能产生优秀的后代,而变异的话产生优秀后代的可能性极低,不过也有存在可能一下就变异出非常优秀的后代。这也是符合自然界生物进化的特征的。
举个栗子:
交叉的过程需要从上一代的染色体中寻找两条染色体,一条是爸爸,一条是妈妈。然后将这两条染色体的某一个位置切断,并拼接在一起,从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因,也包含了一定数量的妈妈的基因。
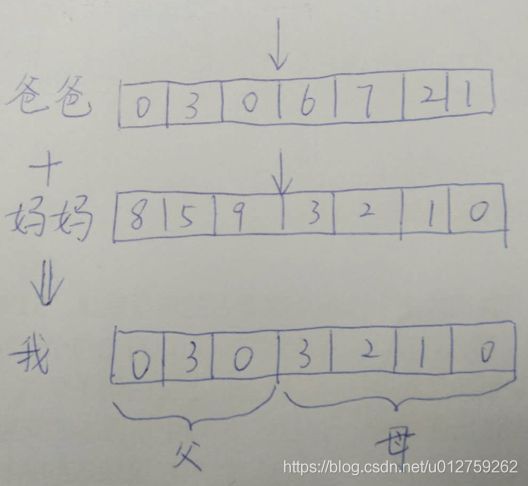
如何从上一代染色体中选出爸爸和妈妈的基因呢?这不是随机选择的,一般是通过轮盘赌算法完成。
在每完成一次进化后,都要计算每一条染色体的适应度,然后采用如下公式计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。
染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和
3.遗传算法流程
4 pytorch版本
import numpy as np
import matplotlib.pyplot as plt
import torch
"""
The y=target is to maximize this equation ASAP:
y = w1x1+w2x2+w3x3+w4x4+w5x5+w6x6
where (x1,x2,x3,x4,x5,x6)=(4,-2,3.5,5,-11,-4.7)
What are the best values for the 6 weights w1 to w6?
We are going to use the genetic algorithm for the best possible values after a number of generations.
"""
def cal_pop_fitness(equation_inputs, population):
'''
# Calculating the fitness value of each solution in the current population.
# The fitness function calulates the sum of products between each input and its corresponding weight.
:param equation_inputs: 输入值
:param population: 代表种群的矩阵
:return:
'''
# fitness = ((population.sub(equation_inputs)) ** 2).mean(dim=1)
fitness = torch.mm(population, equation_inputs.t())
return fitness
def select_mating_pool(population, fitness, num_parents):
'''
选择最佳的父母双亲
:param population: 代表种群的矩阵
:param fitness: 每个个体根据适应度函数计算的结果
:param num_parents: 需要保留双亲的数量
:return:
'''
fitness = fitness.numpy()
population = population.numpy()
# Selecting the best individuals in the current generation as parents for producing the offspring of the next generation.
parents = np.empty((num_parents, population.shape[1]))
for parent_num in range(num_parents):
max_fitness_idx = np.where(fitness == np.max(fitness))
max_fitness_idx = max_fitness_idx[0][0]
parents[parent_num, :] = population[max_fitness_idx, :]
return torch.Tensor(parents)
def crossover(parents, offspring_size):
'''
杂交
:param parents: 代表双亲的矩阵
:param offspring_size: 需要产生后代的数量
:return:
'''
parents = parents.numpy()
offspring = np.empty(offspring_size)
crossover_point = np.uint8(offspring_size[1] / 2)
for k in range(offspring_size[0]):
print(k)
# Index of the first parent to mate.
parent1_idx = k % parents.shape[0]
# Index of the second parent to mate.
parent2_idx = (k + 1) % parents.shape[0]
# The new offspring will have its first half of its genes taken from the first parent.
offspring[k, 0:crossover_point] = parents[parent1_idx, 0:crossover_point]
offspring[k, crossover_point:] = parents[parent2_idx, crossover_point:]
return torch.Tensor(offspring)
def mutation(offspring_crossover, num_mutations):
'''
变异操作
:param offspring_crossover: 代表变异后孩子的数量
:param num_mutations: 发生变异的特征的数量
:return:
'''
offspring_crossover = offspring_crossover.numpy()
mutations_counter = np.uint8(offspring_crossover.shape[1] / num_mutations)
# Mutation changes a number of genes as defined by the num_mutations argument. The changes are random.
for idx in range(offspring_crossover.shape[0]):
gene_idx = mutations_counter - 1
for mutation_num in range(num_mutations):
# The random value to be added to the gene.
random_value = np.random.uniform(-1.0, 1.0, 1)
offspring_crossover[idx, gene_idx] = offspring_crossover[idx, gene_idx] + random_value
gene_idx = gene_idx + mutations_counter
return torch.Tensor(offspring_crossover)
def oneStep(equation_inputs, features, population, num_parents, num_children, num_mutations):
'''
运行一次的结果
:param equation_inputs: 输入值
:param features: 特征值
:param population: 代表种群的矩阵
:param num_parents: 双亲的数量
:param num_children: 产生孩子的数量
:param num_mutations: 变异的数量
:return:
'''
# 3. 确定适应度函数
fitness = cal_pop_fitness(equation_inputs, population)
# 4. 选出最好的 num_parents 双亲
parents = select_mating_pool(
population, fitness, num_parents
)
# print("Parents")
# print(parents)
# 5. Generating next generation using crossover.
offspring_crossover = crossover(
parents,
offspring_size=(
num_children,
features
)
)
# print("Crossover")
# print(offspring_crossover)
# 6. Adding some variations to the offspring using mutation.
offspring_mutation = mutation(offspring_crossover, num_mutations)
# print("Mutation")
# print(offspring_mutation)
# 7. Creating the new population based on the parents and offspring.
new_population = torch.cat((parents, offspring_mutation), 0)
print("new_population")
print(new_population)
return new_population, fitness
主函数
def main():
equation_inputs = np.array([[4, -2, 3.5, 5, -11, -4.7]])
# 猜测数据的上下限
upper_limit = 9
low_limit = 0
# 数据精度
precision = 4
# 种群数量
# pop_size = (upper_limit - low_limit) * pow(10, precision)
pop_size = 8
# 特征数量
features = equation_inputs.shape[1]
# 父母保留下来的数量
selection = 0.5
# 迭代次数
generations = 1000
# num_mutations = int(1. / pop_size * features)
num_mutations = 1
num_parents = int(pop_size * selection)
num_children = pop_size - num_parents
# 2. 初始化种群
population = np.random.uniform(low=-4.0, high=4.0, size=(pop_size, features))
equation_inputs = torch.Tensor(equation_inputs)
population = torch.Tensor(population)
best_outputs = []
for generation in range(generations):
population, fitness = oneStep(
equation_inputs, features, population,
num_parents, num_children, num_mutations
)
best_outputs.append(np.max(np.sum(population.numpy() * equation_inputs.numpy(), axis=1)))
print('population')
print(population)
fitness = cal_pop_fitness(equation_inputs, population)
print(fitness)
print("GA's output")
print(best_outputs)
5. 参考资料
- 如何通俗易懂地解释遗传算法?有什么例子?
- 10分钟搞懂遗传算法(含源码)