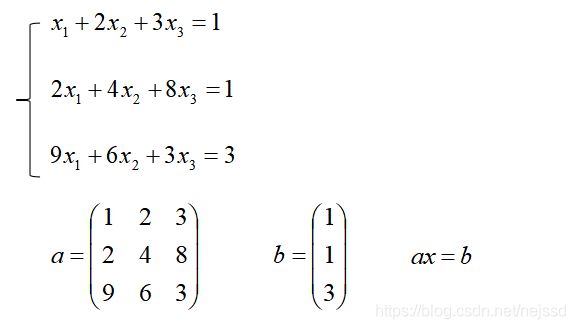python求解各种复杂的线性/非线性方程组

Python求解各种复杂的线性/非线性方程组

本文将要介绍几种方法去求解各种复杂的方程组，包括实数域和复数域的线性、非线性方程组，并对比这几种方法的优缺点。本文用到了numpy、scipy、sympy这三个科学计算包。

一、线性方程组。

线性方程组可以用numpy去求解。
1.实数域。

import numpy as np
a=np.mat('1,2,3;2,4,8;9,6,3')
b=np.mat('1;1;3')
c=np.linalg.solve(a,b)

输出如下：

2.复数域。

import numpy as np
a=np.mat('1,-1j;1j,-1')
b=np.mat('1;1')
c=np.linalg.solve(a,b)

输出如下：

二、非线性方程组。

scipy和sympy不但可以解线性方程(组)，还可以求解非线性方程(组)，但是也有各自的优缺点。

1.scipy求解

scipy.optimize里面有两个函数可以数值求解方程组，分别是root和solve，这两个函数会找到方程组的一个近似解。下面通过例子介绍这两个函数的使用。

(1).root
scipy.optimize.root(fun, x0, args=(), method=‘hybr’, jac=None, tol=None, callback=None, options=None)
其中参数fun是一个函数，你需要定义这个函数，并且你定义的这个函数返回一个方程组。 参数x0是方程组解的初始猜测值，是必须要指定的参数，root函数将找到最靠近x0的一个解。参数args是函数fun的额外参数。参数method默认是‘hybr’，此参数还可以取 ‘lm’ ‘broyden1’ ‘broyden2’ ‘anderson’ ‘linearmixing’ ‘diagbroyden’ ‘excitingmixing’ ‘krylov’ ‘df-sane’，代表采用不同的算法去求解。参数tol可以认为是精度。

先来看看实数域的例子

from scipy.optimize import root

def f1(x):
   return [x[0]+x[0]*x[1]-2,x[0]-x[1]-2]
   
print(root(f1,[0,-1]).x)#初始猜测值[0,-1]
print(root(f1,[0,0]).x)#初始猜测值[0,0]

输出如下：

求出的近似解与真解相差非常小。设置不同的初始猜测值可能得到不同的解，这是因为有的方程组的解不一定只有一个，可能有多个解，root函数会得到最接近初始猜测值的一个解。

此外，在上面的基础上我们可以设置参数jac来提高运算速度（尤其是计算量很大时效果很明显）。
我们需要再定义一个函数，这个函数返回值是方程组对应的雅可比矩阵，通过下面的例子说明。

from numpy import array,mat,sin,cos,exp
from scipy.optimize import root

def f(x):
    eqs=[]
    eqs.append(x[0]*x[1]+x[1]*x[2]+sin(x[0])*exp(x[1])+x[1])
    eqs.append(x[0]*x[1]-exp(x[0])*x[1]+1)
    eqs.append(x[1]*x[2]+exp(x[1])*x[2]+1) 
    return eqs

def jac1(x):#方程组对应的雅可比矩阵
    return mat([[x[1]+cos(x[0])*exp(x[1]), x[0]+x[2]+sin(x[0])*exp(x[1])+1, x[1]],
                [x[1]-exp(x[0])*x[1], x[0]-exp(x[0]), 0],
                [0 ,x[2]+exp(x[1])*x[2], x[1]+exp(x[1])]])

print(root(f,[0,0,0]).x)
print(root(f,[0,0,0],jac=jac1).x)#加上参数jac加快运算速度

输出如下：

再来看一个复数域的例子

如果不设置参数method，它默认是‘hybr’，即用改进的Powell hybrid算法求解，它不适用于复数域。此时我们不能再用上面的办法，我们可以设置参数method=‘krylov’ (此算法牺牲精度换取速度，有利有弊)

from scipy.optimize import root

def f1(x):
    return [x[0]*(1j)+x[0]*x[1]+1,x[0]+x[1]-1j]

print(root(f1,[1,1],method='krylov').x)
print(root(f1,[1,1],method='krylov',tol=1e-10).x)#设置能够允许的误差为10的-10次方

输出如下：

第一行输出没有设置参数tol，得到的解与真解的差别还是有一点的。
第二行输出我们设置了参数tol是10的-10次方，得到的解与真解的差别就相当小了。
另外method参数也可以设为别的，解复数域的非线性方程组建议用method=‘krylov’，它不需要雅可比矩阵，它在处理很庞大、变量很多的方程组时比较好用。

(2).fslove
fsolve的用法和root很类似，但是它的功能不如root全面，fsolve其实就是用hybr算法求解, 因此它不能解复数域的方程组。下图可以看出fsolve和root的差别：

可见，fsolve只是root的一小部分。

scipy.optimize.fsolve(func, x0, args=(), fprime=None, full_output=0, col_deriv=0, xtol=1.49012e-08, maxfev=0, band=None, epsfcn=None, factor=100, diag=None)
（其中参数fprime对应雅可比矩阵，其余参数和root函数基本一样。）

from scipy.optimize import fsolve
from numpy import array,mat

def f1(x):
  return [x[0]+x[0]*x[1]-2,x[0]-x[1]-2]

def jac1(x):#方程组对应的雅可比矩阵
  return mat([[1+x[1],x[0]],[1,-1]])

print(fsolve(f1,[0,-1]))#初始猜测值[0,-1]
print(fsolve(f1,[0,-1],fprime=jac1))#初始猜测值[0,-1],并设置参数prime
print(fsolve(f1,[0,0]))#初始猜测值[0,0]
print(fsolve(f1,[0,0],fprime=jac1))#初始猜测值[0,0],并设置参数prime

2.sympy求解

sympy中的solve函数可以严格求解某些方程组，nsolve可以数值求近似解。
(1).solve
直接看一个复数域的例子：

from sympy import symbols,Eq,solve
x0,x1=symbols('x0 x1')
eqs=[Eq(x0*(1j)+x0*x1,-5),Eq(x0+x1,1j)]
print(solve(eqs,[x0,x1]))

输出如下：

solve函数就会找到所有的解。但是像超越方程之类的不存在求根公式的方程，solve函数是不能求解的，只能数值求解，要用nsolve函数。
(2).nsolve
nsolve函数需要指定一个初始猜测解。

from sympy import symbols,Eq,nsolve
x0,x1=symbols('x0 x1')
eqs=[Eq(x0*(1j)+x0*x1,-5),Eq(x0+x1,1j)]
print(nsolve(eqs,[x0,x1],[1,1]))#初始猜测解设为[1，1]

输出如下：
nsolve有时候并不是很好使，初始猜测解设的不好，它有可能找不到解。

三、scipy和sympy的优缺点分析。

1.scipy.optimize.root求解方程组速度很快，尤其是加上参数jac或参数method='krylov’时，求解大型方程组速度会很明显的比其它办法快，即使是1000个变量的方程组，它也能很快解完。但是有的方程组有多解(比如二次方程有俩根)，而scipy.optimize.root只能得到靠近初始猜测值的那个解。
2.对一些形式比较简单的、有求根公式的方程，sympy.solve虽然能得到它所有的严格解，但是当方程组变量较多时，它求起来会很慢。而且对于不存在求根公式的复杂方程，sympy.solve是求不了的，这时要用sympy.nsolve的求数值解，速度也比scipy.optimize.root慢很多。

四、总结

1.线性方程组用numpy.linalg.solve足矣。（实数域复数域都可以）
2.求解非线性方程组，如果存在求根公式的且未知量数目较少的方程组，可以用sympy求。如果是很庞大且形式较复杂的方程组，用scipy.optimize.root数值求解，最好写出雅可比矩阵以提高运算速度。(如果你懒得写雅可比矩阵，就设置参数method=‘krylov’，解起来速度也很快，只不过精度不高)。

最后展示一段代码，测试一下scipy.optimize.root的求解速度，这里是求解含有400个未知量的非线性方程组，求解20次。

from numpy import array,arange,sin,cos,sqrt,exp,pi,meshgrid,dtype,linalg,zeros
from scipy.optimize import root,fsolve
from matplotlib.pyplot import figure,xlabel,ylabel,show,text
from mpl_toolkits.mplot3d import Axes3D
from time import time

def run(m,n,marker=None):
  v=1
  L,T=pi,1
  h,tao=L/m,T/n
  mlist=arange(0,m+1)
  nlist=arange(0,n+1)
  f=lambda x,t:exp(-2*t)*sin(x)*cos(x)
  phi=lambda x:sin(x)
  realsolve=lambda x,t:exp(-t)*sin(x)
  mysolves=[phi(mlist*h)]
  
  def u(x,ii,j):
      if j==1:
          return x[ii]
      elif j==1/2:
          return (x[ii]+x_former[ii])/2
      elif j==0:
          return x_former[ii]
      else:
          print("error")

  def jac(x):#雅可比矩阵
      a=zeros((m+1,m+1))
      a[0][0]=1
      a[-1][-1]=1
      for i in range(1,m):
        a[i][i-1]=1/6/h*((x[i+1]+x_former[i+1])/2-(x[i-1]+x_former[i-1])/2-((x[i-1]+x_former[i-1])/2+(x[i]+x_former[i])/2+(x[i+1]+x_former[i+1])/2))-v/(2*h*h)
        a[i][i]=1/tao+1/6/h*((x[i+1]+x_former[i+1])/2-(x[i-1]+x_former[i-1])/2)+v/(h*h)
        a[i][i+1]=1/6/h*((x[i+1]+x_former[i+1])/2-(x[i-1]+x_former[i-1])/2+((x[i-1]+x_former[i-1])/2+(x[i]+x_former[i])/2+(x[i+1]+x_former[i+1])/2))-v/(2*h*h)
      
      return a
    
  def eqsgroup(x):
      eqs=[x[0]]
      for i in range(1,m):
         eqs.append(1/tao*(u(x,i,1)-u(x,i,0))+1/(6*h)*(u(x,i-1,1/2)+u(x,i,1/2)+u(x,i+1,1/2))*(u(x,i+1,1/2)-u(x,i-1,1/2))-v/h/h*(u(x,i-1,1/2)-2*u(x,i,1/2)+u(x,i+1,1/2))-f(i*h,k*tao) )#
      eqs.append(x[m])
      return array(eqs)

  x_former=phi(mlist*h)
  start=time()
  for k in arange(0,n):
      #x_former=fsolve(eqsgroup,x_former,fprime=jac)
      x_former=root(eqsgroup,x_former,jac=jac).x
      mysolves.append(list(x_former))
  print('scipy计算时间为',time()-start,'秒')
  
  x,y=mlist*h,nlist*tao
  x,y=meshgrid(x, y)
  z=array(mysolves,dtype=dtype('float32'))
  z2=array(realsolve(x,y))
  dz=z-z2
  ekmax=array(linalg.norm(dz,axis=1)*sqrt(h)).max()
  
  fig = figure(figsize=(15, 10),dpi=80)
  axes3d = Axes3D(fig)
  axes3d.set_title(r'$h=\pi/$'+str(m)+r'  $\tau=1/$'+str(n),color = 'black',size = 30)  
  axes3d.plot_surface(x,y,z)
  axes3d.plot_surface(x,y,z2)
  xlabel('x',color = 'black',size = 30)
  ylabel('t',color = 'black',size = 30)
  axes3d.set_xlim(0,pi)
  axes3d.set_xticks([0,pi/4,pi/2,0.75*pi,pi])
  axes3d.set_xticklabels([0, r'$\frac{\pi}{4}$', r'$\frac{\pi}{2}$', r'$\frac{3\pi}{4}$', r'$\pi$'],size=20)
  axes3d.set_zlabel(r'$U(x,t)$',color = 'black',size=30)
  axes3d.set_zticks(arange(0,1,0.1))
  axes3d.set_zticklabels([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9],size=13)
  show()


run(400,20)

scipy只需2秒就解完，而如果用sympy去解，会非常慢。