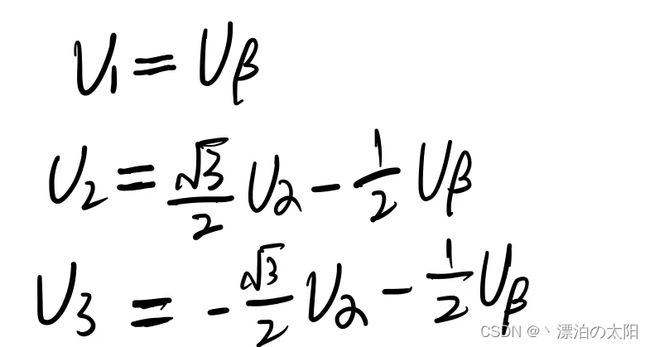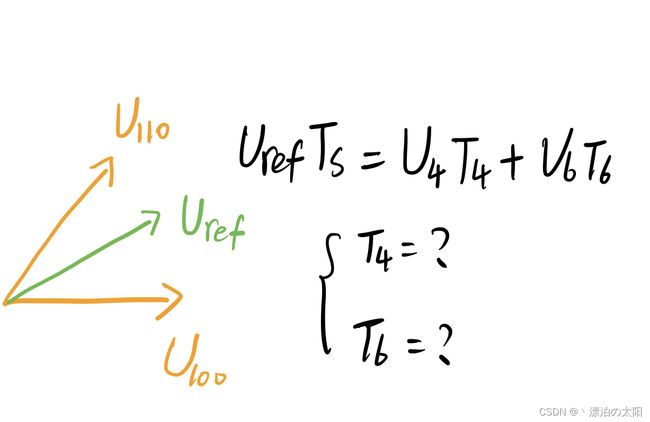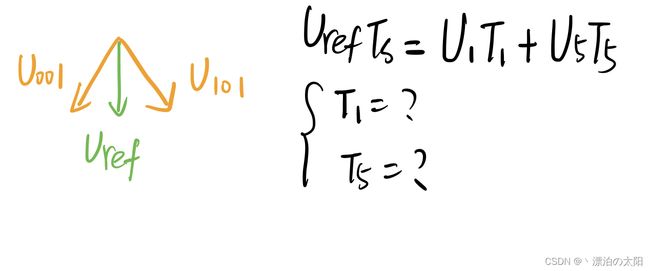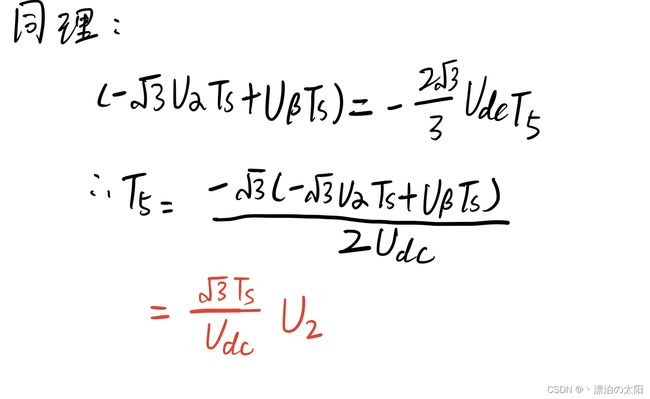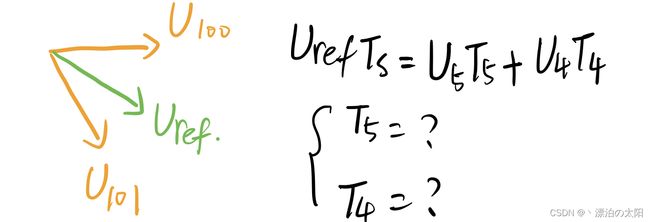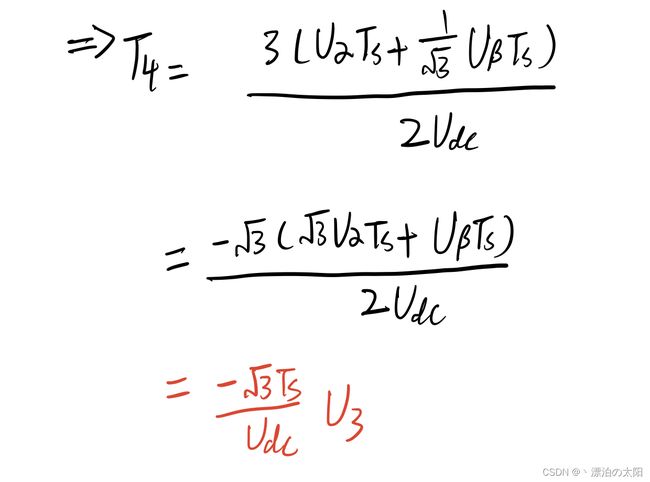【电机控制算法】SVPWM算法的应用(基于Simulink与STM32外设场景的仿真)
文章目录
- 前言
- 一、扇区判断
- 二、各扇区基础矢量作用时间的计算
-
- 1.若处于扇区I
- 2.若处于扇区II
- 3.若处于扇区III
- 4.若处于扇区IV
- 5.若处于扇区V
- 6.若处于扇区VI
- 7.In a word
- 三、STM32的外设场景
-
- 1. TIMx的计数器CNT
- 2. TIMx的输入捕获寄存器CCRx
- 3. TIMx的两种PWM模式
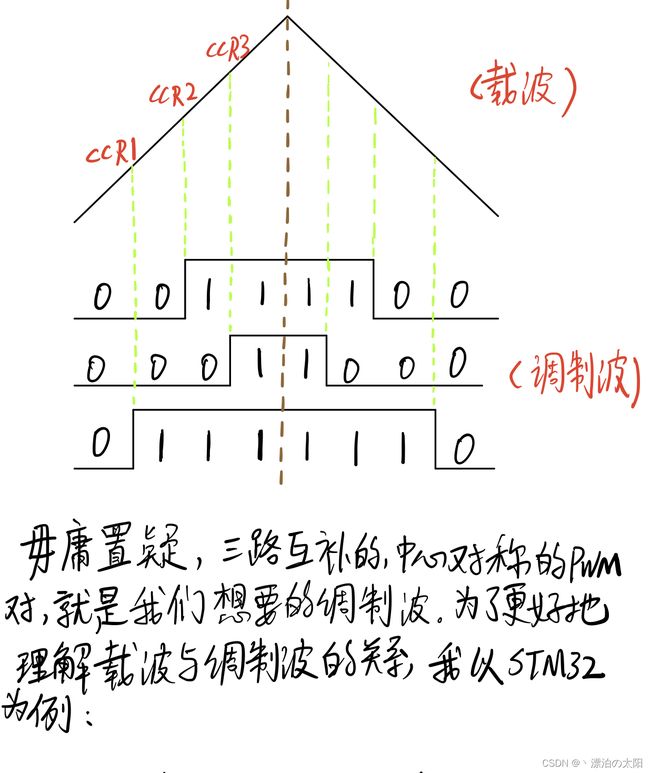
- 四、互补输出且呈中心对称的PWM对
- 五、载波和调制波
- 六、观察相应扇区的3对PWM波形
-
- 1.扇区I
- 2.扇区II
- 3.扇区III
- 4.扇区IV
- 5.扇区V
- 6.扇区VI
- 7.In a word
- 七、Simulink编程仿真
-
- 1. 输入与输出
- 2. MATLAB编程
- 3. 利用SVPWM算法的输出搭建中心对称且互补的PWM生成器
- 4.仿真结果与波形
前言
笔者写下此文的目的,是为了记录在MCU中实现七段式SVPWM最简单最高效率的计算方法,所以本文并不会把重点放在理解SVPWM上,而是适当推导,利用最终结论,并结合STM32的硬件场景,去编写SVPWM算法。
若您的重点是在于理解SVPWM的由来和始末,相信其他文章能够讲得比笔者更好。

一、扇区判断
我们需要知道电机转子当前所在的扇区,下一步才能生成与转子形成一定相位差的定子磁场,吸引转子以最大的力矩旋转。这时候需要利用到两相静止坐标轴(2s)的电压值 Vα和Vβ.
我们定义:
不难发现,U1+U2+U3=0。在芯片中编程时,可以使用这个关系对U2或者U3的表达式进行简化,从而避免更多的乘除法运算(因为更耗时)。
再定义:
若U1>0,A=1;否则A=0;
若U2>0,B=1;否则B=0;
若U3>0,C=1;否则C=0;
存在关系式: N=4C+2B+A
真值表:
| N | 3 | 1 | 5 | 4 | 6 | 2 |
|---|---|---|---|---|---|---|
| 扇区sector | I | II | III | IV | V | VI |
二、各扇区基础矢量作用时间的计算
对于矢量,都是可以合成的。定义Uref为合成矢量,Ts为一个作用周期(也就是一个中心对称的互补PWM对的周期):
1.若处于扇区I
2.若处于扇区II
3.若处于扇区III
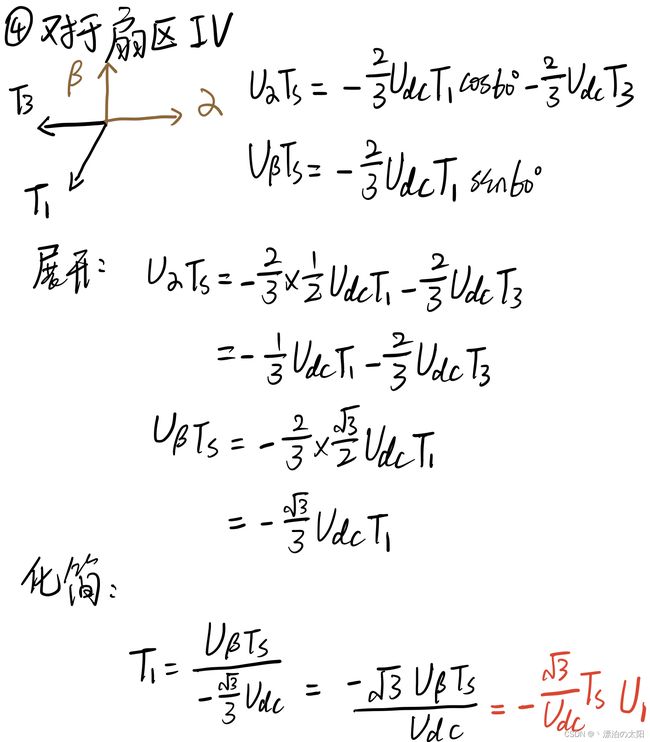
4.若处于扇区IV
5.若处于扇区V
6.若处于扇区VI
7.In a word
| 扇区sector | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| 作用时间1 | T4=K*U2 | T2=-K*U2 | T2=K*U1 | T1=-K*U1 | T1=K*U3 | T4=-K*U3 |
| 作用时间2 | T6=K*U1 | T6=-K*U3 | T3=K*U3 | T3=-K*U2 | T5=K*U2 | T5=-K*U1 |
若Ts>作用时间1+作用时间2,那么,剩下的作用时间都平均分配给了两个零矢量。T(000)=T(111)=0.5 *(Ts-作用时间1-作用时间2)。
当Ts=作用时间1+作用时间2,T(000)=T(111)=0;
三、STM32的外设场景
关于定时器PWM输出机制的理解上,还请翻阅:STM32定时器的单路PWM输出。
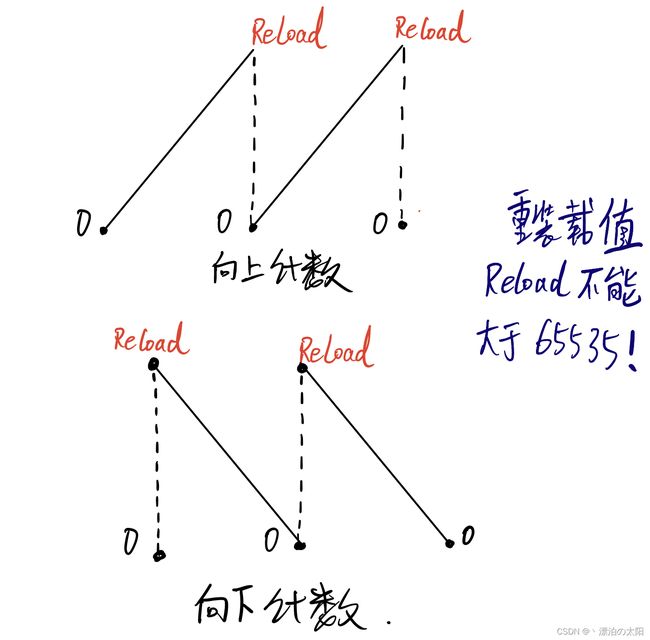
1. TIMx的计数器CNT
2. TIMx的输入捕获寄存器CCRx
CCRx是指:当CNT计数到CCRx寄存器存储的计数值时,CHx的电平发生转换,有个图更形象:
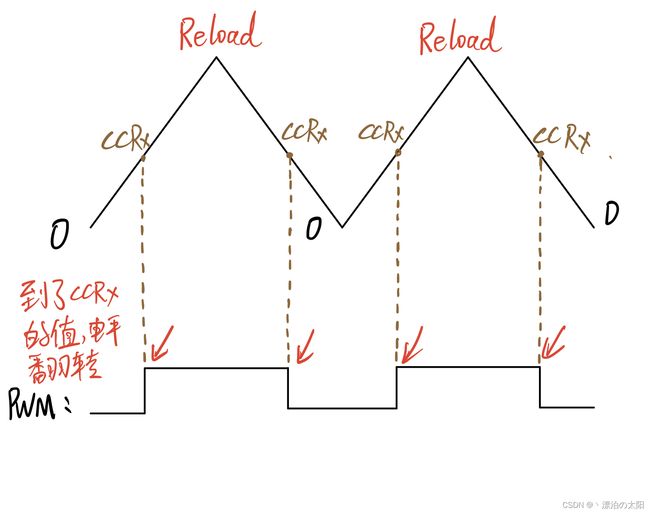
3. TIMx的两种PWM模式
STM32主要有两种PWM发波模式。
PWM模式1:
CNT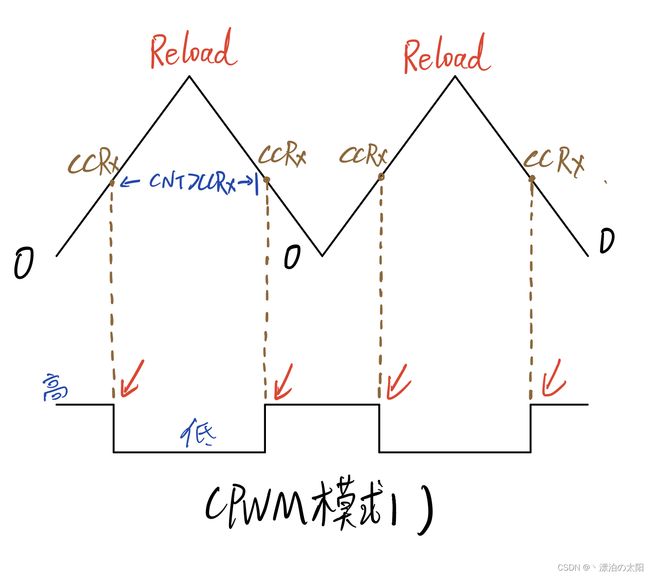
PWM模式2:
CNT>CCR,CHx高电平,否则CHx低电平

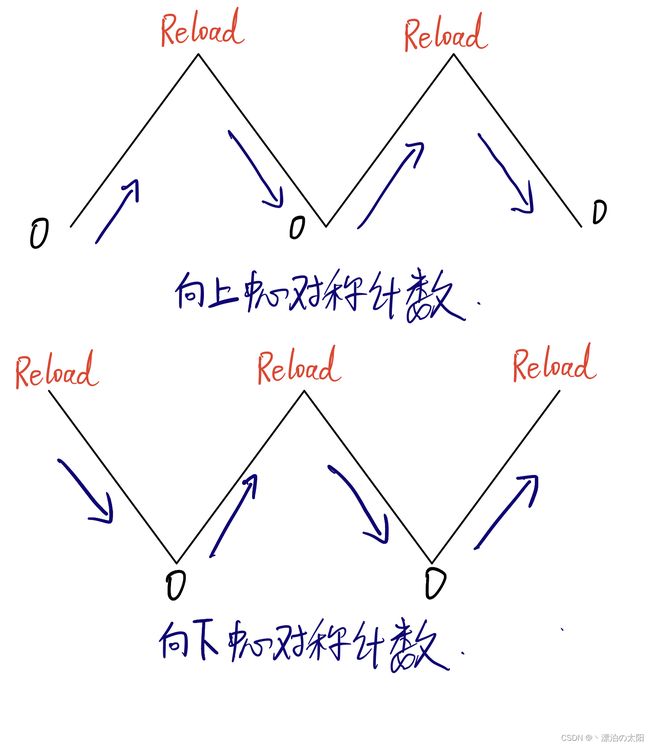
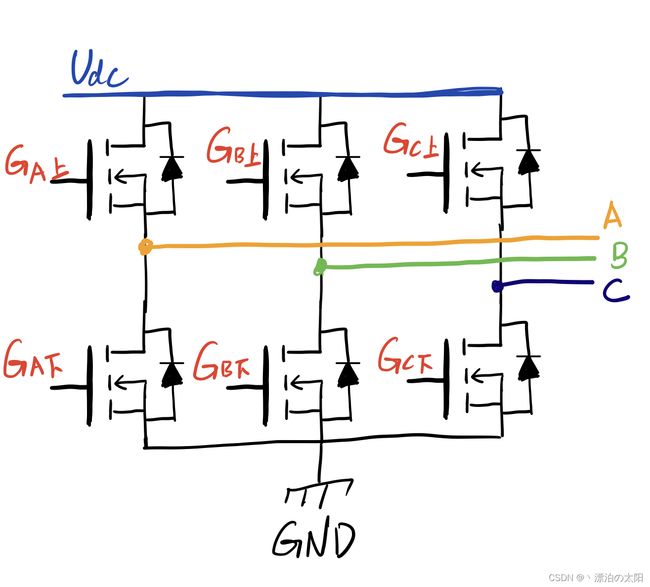
四、互补输出且呈中心对称的PWM对
以CNT向上计数,PWM2模式为例。我们看看外设的应用场景。
单路非中心对称的PWM输出:

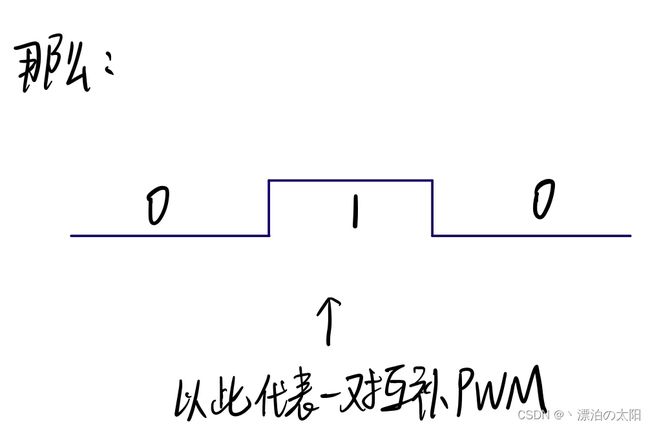
而互补输出且呈中心对称的PWM:

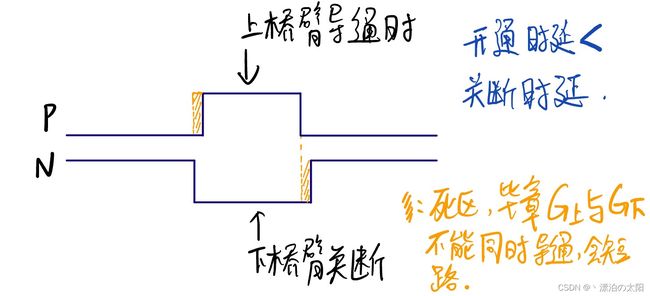
一般的MOS管,它的关断时间大于开通时间很多,反向恢复时间则更长,编程时往往选最大的时延考虑。
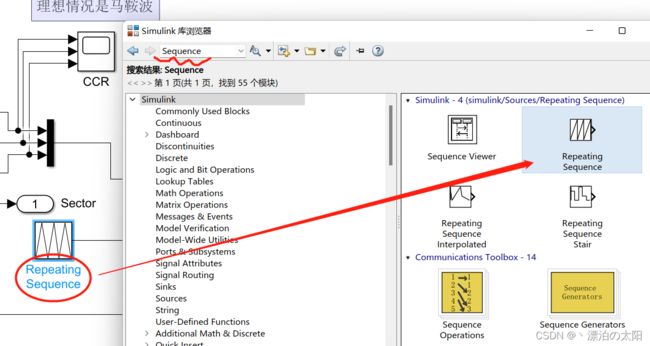
五、载波和调制波
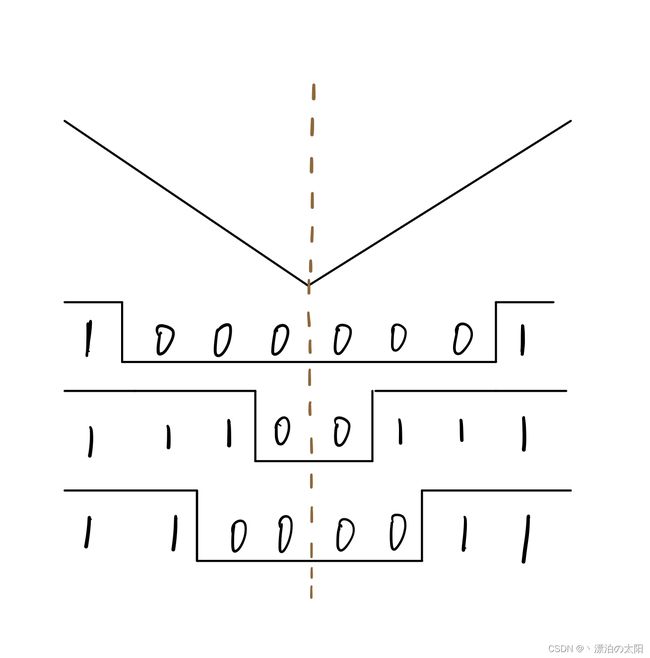
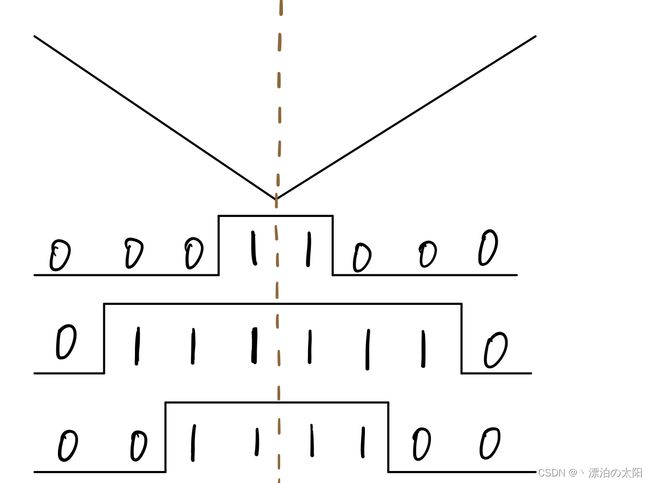
六、观察相应扇区的3对PWM波形
波形由上到下依次是A,B,C三相。
1.扇区I

更正:Tx定义为零矢量后先发送的矢量的作用时间,Ty定义为其后发生的矢量的作用时间.
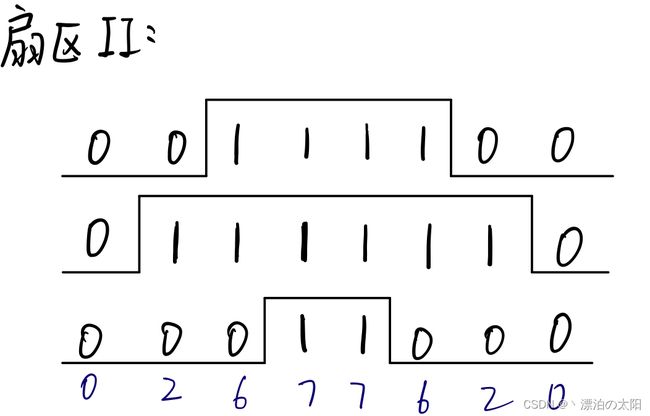
2.扇区II
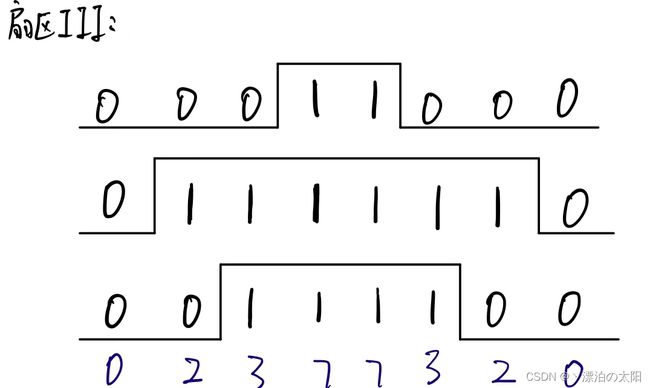
3.扇区III
4.扇区IV
5.扇区V
6.扇区VI
7.In a word
| 扇区sector | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| CCR1 | Ta | Tb | Tc | Tc | Tb | Ta |
| CCR2 | Tb | Ta | Ta | Tb | Tc | Tc |
| CCR3 | Tc | Tc | Tb | Ta | Ta | Tb |
这里留给读者自行推理,只要明白了例子,很快就能理解CCRx在不同模式下正确的赋值
七、Simulink编程仿真
1. 输入与输出
【需要的输入】
SVPWM的输入是反Park变换中得到的 Vα和Vβ,这两个是最关键的。
次之从我们的公共乘积因子K可知,我们需要输入母线的电压 Udc .
最后,输入我们希望生成的调制波频率 f_PWM .
【我们得到的输出】
① 三路输出比较寄存器CCRx的值
② 扇区
这样,Simulink中Svpwm模组中的函数function就已经确定了:
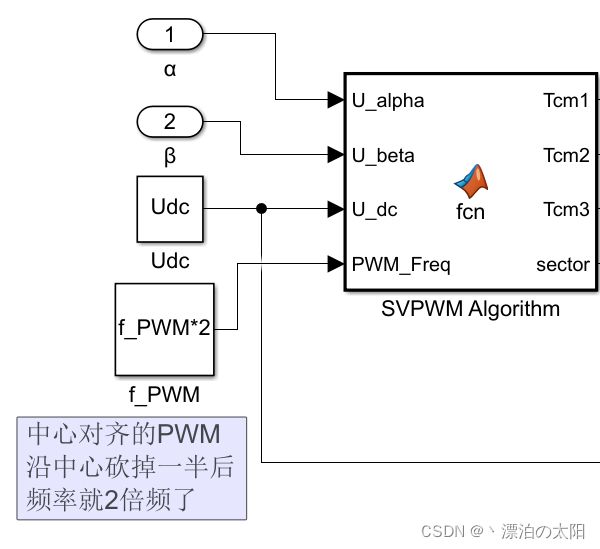
假如我们要求中心对称PWM对的频率是8K,那么他非中心对称的PWM(单路PWM)的频率就是2 * f_PWM,那么,中心对称的PWM到达中点的时间周期就是1/(2 * f_PWM);
2. MATLAB编程
采用载波向上计数,PWM模式2的思想进行搭建,编程。
%4个输入,4个输出
function [Tcm1,Tcm2,Tcm3,sector] = fcn( U_alpha,U_beta,U_dc,PWM_Freq)
%输出参数初始化
sector=0;
Tcm1=0;
Tcm2=0;
Tcm3=0;
%PWM采用中心对齐
%为了避免值过小,默认使用PWM频率的两倍作为载波值
%假如我们希望中心对称PWM的频率是8K,那么他对应的单路PWM频率应该是16K
%所以我们载波CNT的计数最大值是16K
Ts=PWM_Freq;
sqrt_3=sqrt(3);
%判断扇区部分(需要强制类型转换为浮点型)
U1=double(U_beta);
U2=double(sqrt_3*0.5*U_alpha-U_beta*0.5);
U3=double(-sqrt_3*0.5*U_alpha-U_beta*0.5);
%获得对应布尔值
if U1>0
A=1;
else
A=0;
end
if U2>0
B=1;
else
B=0;
end
if U3>0
C=1;
else
C=0;
end
N=4*C+2*B+A;
%根据N的公式结果判断扇区
switch N
case 3
sector=1;
case 1
sector=2;
case 5
sector=3;
case 4
sector=4;
case 6
sector=5;
case 2
sector=6;
end
%不同扇区不同矢量的作用时间计算
K=sqrt_3*Ts/U_dc;%公共乘积因子
switch (sector)
case 1
Tx=K*U2;
Ty=K*U1;
case 2
Tx=-K*U2;
Ty=-K*U3;
case 3
Tx=K*U1;
Ty=K*U3;
case 4
Tx=-K*U1;
Ty=-K*U2;
case 5
Tx=K*U3;
Ty=K*U2;
case 6
Tx=-K*U3;
Ty=-K*U1;
otherwise
Tx=0;
Ty=0;
end
%过调制算法
if (Tx+Ty)>Ts
Tx=Ts*Tx/(Tx+Ty);
Ty=Ts*Ty/(Tx+Ty);
else
Tx=Tx;
Ty=Ty;
end
%零矢量总作用时间的二分之一,也就是T0和T7的值
T0=(Ts-Tx-Ty)*0.5;
%见六中的总结
Ta=T0*0.5; %先跳转的PWM对的输出比较值
Tb=Ta+0.5*Tx; %后跳转的PWM对的输出比较值
Tc=Tb+0.5*Ty; %最后跳转的PWM对的输出比较值
%根据六中的扇区情况,赋值三路PWM对的输出比较值
switch sector
case 1
Tcm1=Ta;
Tcm2=Tb;
Tcm3=Tc;
case 2
Tcm1=Tb;
Tcm2=Ta;
Tcm3=Tc;
case 3
Tcm1=Tc;
Tcm2=Ta;
Tcm3=Tb;
case 4
Tcm1=Tc;
Tcm2=Tb;
Tcm3=Ta;
case 5
Tcm1=Tb;
Tcm2=Tc;
Tcm3=Ta;
case 6
Tcm1=Ta;
Tcm2=Tc;
Tcm3=Tb;
end
end
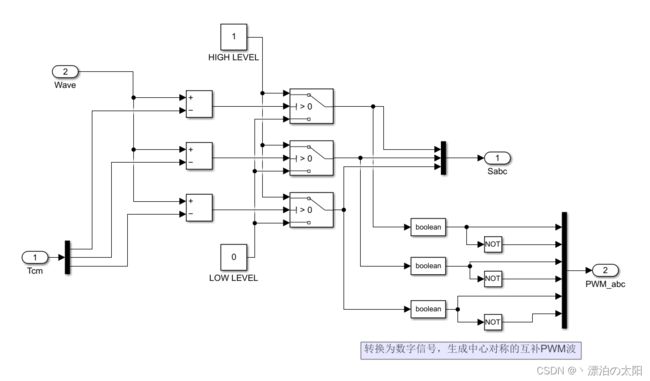
3. 利用SVPWM算法的输出搭建中心对称且互补的PWM生成器
总图:
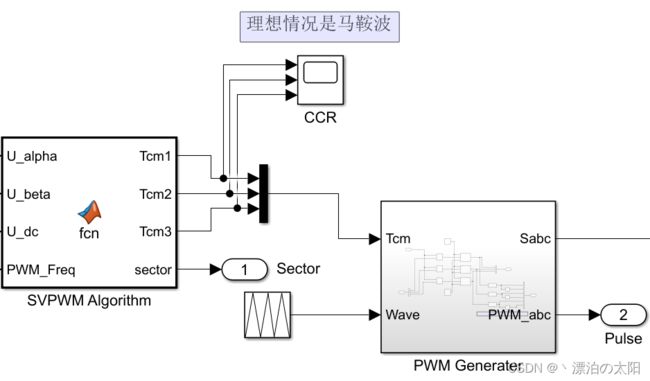
【需要的输入】
① 三路输出比较寄存器CCRx的值
② 模拟CNT计数的三角波作为载波
【获得的输出】
三路互补且中心对称的PWM波,用于控制开关管
载波从0到1/(2 * f_PWM)时间,到达最大的计数值f_PWM。对应的是中心对称PWM周期的时间中点,即0.5Ts。
笔者这里使用数字量去代表时间,数字量拟用PWM频率代替,比如8K的PWM频率,它的Ts=2PWM_Freq,那么它的时间中点就是f_PWM,这个也类似STM32的重装载值(最大65535);
4.仿真结果与波形
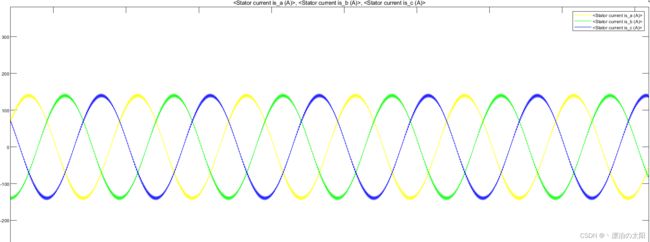
黄色表示A相
绿色表示B相
蓝色表示C相
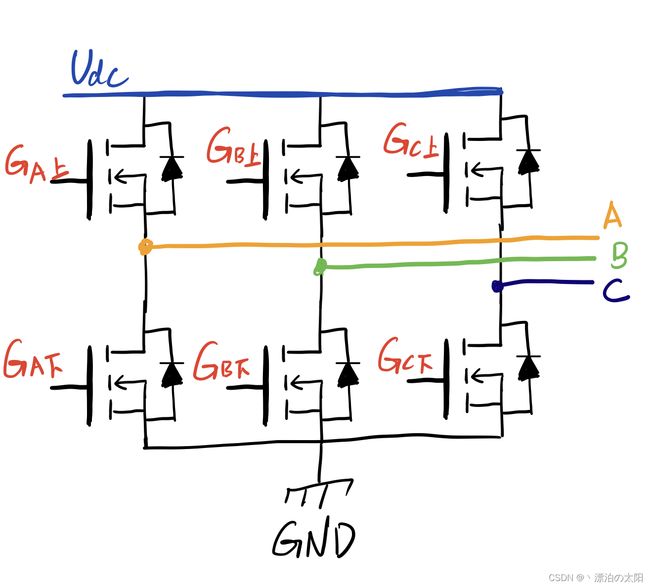
CCRx的波形是马鞍波,而调制波直接输出到PMSM电机的三端上,所以端电压(端对地GND的电压,不是相电压)也是马鞍波!
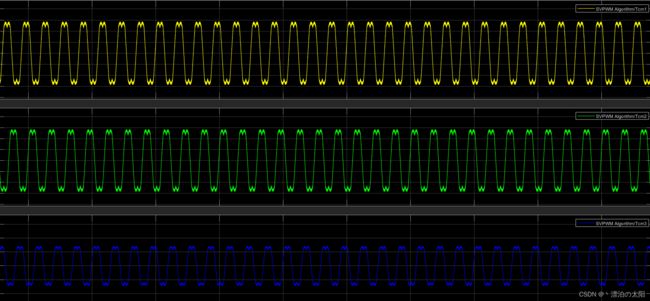
中心对称的PWM对,作用在相上,会使用数字正弦波来等效模拟正弦波;
当然这个仿真可以通过CCRx的值作处理来获得,使用以下公式:
Un_A=double(Udc/3*(2*PWM_a-PWM_b-PWM_c));
Un_B=double(Udc/3*(2*PWM_b-PWM_a-PWM_c));
Un_C=double(Udc/3*(2*PWM_c-PWM_a-PWM_b));
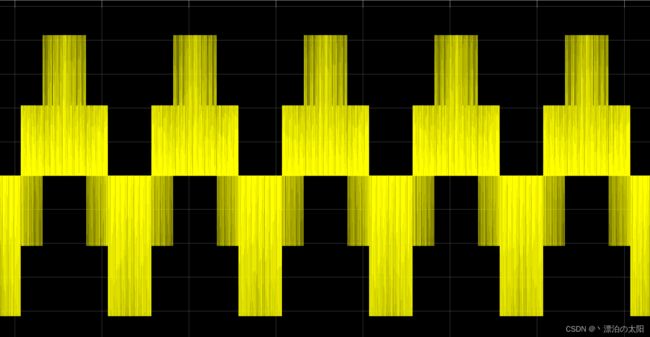

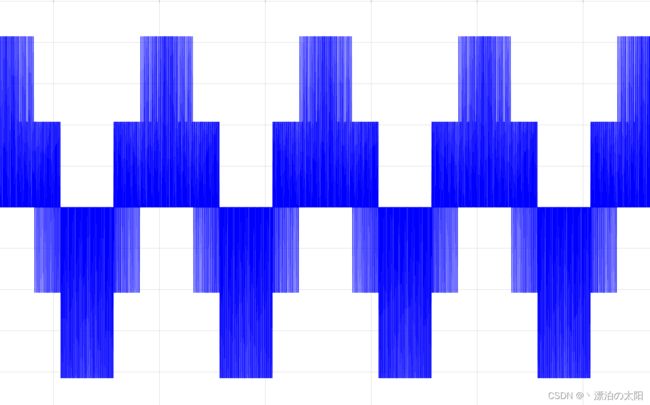
这种数字正弦波,作用在电机上,感性负载的电流惯性,使电机产生与数字正弦波电压有一定相角差的正弦电流,同时三相的电流也是120°对称的。因为是数字正弦波,在正弦电流上我们可以看到一丝丝纹波,这是正常的。
作用在电机上的相电流: