统计基础：3.3_假设检验之t检验（Student‘s t test）

一、参数检验：T检验介绍

  t检验，亦称student t检验（Student’s t test），主要用于样本含量较小（例如n < 30），总体标准差σ未知的正态分布。 [1] t检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。

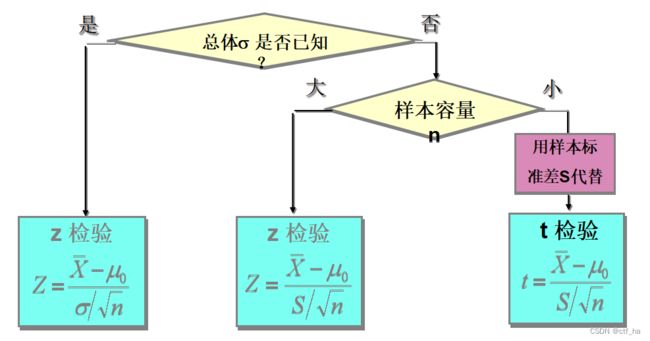
1.1、单样本T检验(one sample t test)

  单样本T检验又称单样本均数t检验,适用于样本均数与已知总体均数μ0的比较,目的是检验样本均数所代表的总体均数μ是否与已知总体均数μ0有差别。

前提条件：总体标准α未知的小样本,且服从正态分布

  单样本t检验统计量为：
$$t=\frac{\bar{X}-u}{S/\sqrt{n}}$$
  其中$\bar{X}$ 为样本平均数， $S=\sqrt{\frac{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}{n}}$为样本标准偏差，n为样本数。该统计量t在零假说：μ=μ0为真的条件下服从自由度为n的t分布。

eg:大规模调查已知某地新生儿出生体重为3.30kg。从该地难产儿中随机抽取35名新生儿,平均出生体重为3.42kg,标准差为0.40kg,问该地难产儿出生体重是否与一般新生儿体重不同?
step1：建立假设H0：u=u0,H1:u≠0
step2:计算统计量 $t=\frac{\bar{X}-u_0}{S/\sqrt{n}}=\frac{3.42-3.30}{0.40/\sqrt{3}5}=1.77$
step3：在显著性水平$\alpha =0.05$，本例自由度v=n-1=34下，查表得$t_{0.05/2}(34)=2.032$
step4:统计决策,因t < $t_{0.05/2}(34)$，故P>0.05，按 α=0.05水准，没有发现充足的证据拒绝H0，故差别无统计学意义，尚不能认为该地难产儿与一般新生儿平均出生体重不同。

1.2、独立样本T检验(independent sample t-test)

  独立样本T检验是用于分析定类数据与定量数据之间的关系情况，适合对比两组数据的差异性（如不同性别的两类人群,他们网购满意度是否有差异?），需要特别注意的是，该定类变量为二分类变量（三分类及以上使用方差分析），各分类频数可以不相等。

前提条件：两组数据来自正态分布的群体，数据的方差齐，满足独立性。

• 其统计量为：
  $$t=\frac{{\bar{X}}_1-{\bar{X}}_2}{\sqrt{\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2})}}$$
  其中$S_1^2$和$S_2^2$为两样本方差；

1.3、配对样本T检验(paired t test)

  配对t检验,又称非独立两样本均数t检验, 用来看一组样本在处理前后的平均值有无差异，同时要求配对变量差值呈现正态性分布。其基本步骤为：

• step1提出假设：两种处理的效应相同$H_0:u_d=0$;
• step2:计算各对数据间的差值d，将d作为变量计算均数;
• step3:差值样本均数与已知总体均数μd（μd = 0）比较的单样本t检验,其检验统计量为：
  $$t=\frac{\bar{d}-u_d}{S_{\bar{d}}}=\frac{\bar{d}-0}{S_{\bar{d}}}=\frac{\bar{d}}{S_d/\sqrt{n}}$$
  其中$$S_d=\sqrt{\frac{\sum d^2-\frac{(\sum d{)}^2}{n}}{n-1}}$$
• step4:确定p值，作出推断；

eg:有12名接种卡介苗的儿童，8周后用两批不同的结核菌素，一批是标准结核菌素，一批是新制结核菌素，分别注射在儿童的前臂，两种结核菌素的皮肤浸润反应平均直径(mm)如表所示，问两种结核菌素的反应性有无差别
X1 = [12,14.5,15.5,12,13,12,10.5,7.5,9,15,13,10.5]
X2 = [10,10, 12.5,13,10,5.5,8.5,6.5,5.5,8,6.5,9.5]
d = [2,4,3,-1,3,6.5,2,1,3.5,7,6.5,1]=39

• step1:建立假设检验以及检验水准：$H_0:u_d=0;H_1:u_d\ne 0。\alpha =0.05$
• step2:计算统计量t:$\sum d=39、\sum d^2=195$
  $$t=\frac{\bar{d}}{S_d/\sqrt{n}}=\frac{39/12}{\sqrt{\frac{195-(39{)}^2/12}{12-1}}/\sqrt{1}2}=\frac{3.25}{2.4909/3.464}=4.5195$$
• step3:查表得$t_{0.05/2,11}=2.201$,由于t>$t_{0.05/2,11}$,拒绝H0,则认为结果有显著性差异。

----------扩展------------

1.4、两独立样本T检验(two independent sample t-test)

  两独立样本t 检验，又称成组 t 检验,适用于完全随机设计的两样本均数的比较,其目的是检验两样本所来自总体的均数是否相等。

完全随机设计是将受试对象随机地分配到两组中，每组患者分别接受不同的处理，分析比较处理的效应。

前提条件：两独立样本t检验要求两样本所代表的总体服从正态分布N(μ1，$\sigma 1^2$)和N(μ2，$\sigma 2^2$)，且两总体方差$\sigma 1^2$,$\sigma 2^2$相等,即方差齐性。若两总体方差不等需要先进行变换。

  两独立样本t检验的检验假设是两总体均数相等,即H0：μ1=μ2, 统计量计算公式为：

$$t(v=n_1+n_2-2)=\frac{|{\bar{X}}_1-{\bar{X}}_2|}{S_{{\bar{X}}_1-{\bar{X}}_2}}$$

$$S_{{\bar{X}}_1-{\bar{X}}_2}=\sqrt{S_c^2(\frac{1}{n_1}+\frac{1}{n_2})}$$

$$S_c^2=\frac{\sum X_1^2-\frac{(\sum X_1{)}^2}{n_1}+\sum X_2^2-\frac{(\sum X_2{)}^2}{n_2}}{n_1+n_2-2}$$

$S_c^2$称为合并方差（combined/pooled variance）

eg:25例糖尿病患者随机分成两组，甲组X1单纯用药物治疗，乙组X2采用药物治疗合并饮食疗法，二个月后测空腹血糖(mmol/L)如表所示，问两种疗法治疗后患者血糖值是否相同？
X1 = [8.4,10.5,12.12,13.9,15.3,16.7,18,18.7,20.7,21.1,15.2]
X2 = [5.4,6.4,6.4,7.5,7.6,8.1,11.6,12,13.4,13.5,14.8,15.6,18.7]

• step1建立假设：$H_0:u_1=u_2$ $H_1:u_1\ne u_2$
• step2确定显著性水平$\alpha =0.05$
• step3计算统计量：
    由原始数据得：$n_1=12,\sum X_1=182.5,\sum X_1^2=2953.43,n_2=13,\sum X_2=141.0,\sum X_2^2=1743.16,{\bar{X}}_1=\sum X_1/n_1=182.5/12=15.21,{\bar{X}}_2=\sum X_2/n_2=141/13=10.85$
  代入公式得：
  $$S_c^2=\frac{2953.43-\frac{(182.5{)}^2}{12}+1743.16-\frac{(141.0{)}^2}{13}}{12+13-2}=17.03$$
  $$S_{{\bar{X}}_1-{\bar{X}}_2}=\sqrt{17.03(1/12+1/13)}=1.652$$
  $$t=\frac{15.21-10.85}{1.652}=2.639,v=n_1+n_2-2=23$$
  查t界值表，$t_{0.05/2,23}=2.069$,由于t>$t_{0.05/2,23}$，p<0.05,拒绝H0,故认为两种疗法效果不同。