回归、分类问题----线性模型解决方案(LinearRegression、岭回归、Lasso、Logistic回归、LinearSVC等含图)
文章目录
- 线性模型
-
- 回归问题的线性模型
-
- 线性回归(LinearRegression)
- 岭回归(Ridge)
- Lasso回归
- 分类问题的线性模型
-
- LogisticRegression
- LinearSVC -- 线性支持向量机
- 总结
线性模型
线性模型被广泛应用于实践中,线性模型利用输入特征的 线性函数(linear function) 进行预测。
回归问题的线性模型
线性模型预测的一般公式为:
y = w [ 0 ] ∗ x [ 0 ] + w [ 1 ] ∗ x [ 1 ] + w [ 2 ] ∗ x [ 2 ] + . . . + w [ p ] ∗ x [ p ] + b y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[p]*x[p] + b y=w[0]∗x[0]+w[1]∗x[1]+w[2]∗x[2]+...+w[p]∗x[p]+b
其中 x[0]~x[p]表示单个数据点的特征, w[0]~w[p]表示每个特征所对照的斜率,b为对y轴的偏移。
以下代码可在一维wave数据集上学习参数w[0]和b:
import mglearn
# 训练集的data均为随机生成,线性回归模型通过训练 获得 斜率 w[0]、 偏移量b
mglearn.plots.plot_linear_regression_wave()
运行结果
w[0]: 0.393906 b: -0.031804
许多不同线性回归模型,区别在于如何从训练数据中学习参数w和b,及控制模型复杂度。
线性回归(LinearRegression)
线性回归,又称普通最小二乘法OLS,是回归问题中最简单也最经典的方法。
核心思想:通过寻找参数w和参数b,使得训练集的预测值与真实值y的均方误差最小。
均方误差:训练集的预测值与y真实值的差的平方和再除以样本大小。注意多个样本就有多个差的平方。
sklearn.linear_model库中的 LinearRegression 类实现了该模型。
如下代码涉及了该模型的使用方法、数据可视化、精确度测试:
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成包含60个数据的数据集
X, y = mglearn.datasets.make_wave(n_samples=60)
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#图片画出所有的训练数据点
plt.plot(X_train, y_train, 'o')
# 得到斜率w和偏置量b
lr = LinearRegression().fit(X_train, y_train)
#输出斜率和偏移量
print('lr.coef_: {}'.format(lr.coef_))
print('lr.intercept_: {}'.format(lr.intercept_))
#图片画出线性回归的预测线段
x = np.arange(-3,3)
function_x = lr.coef_[0] * x + lr.intercept_
plt.plot(x, function_x)
#输出该模型对训练集和测试集的预测准确度
print('train score: {}'.format(lr.score(X_train, y_train))) #测试训练集的预测准确度
print('test score: {}'.format(lr.score(X_test, y_test))) #测试测试集的预测准确度
运行结果
lr.coef_: [0.38335783]
lr.intercept_: -0.019271513699491025
train score: 0.6413322464165713
test score: 0.6935781092109214
可见预测结果无论是训练集结果还是测试集结果均不是很好,这是因为该数据集仅有一个特征,出现了欠拟合(即特征量较少无法准确预测)的状态。
接下来,尝试使用更高维的数据集来进行测试,即波士顿房价数据集,包含506个样本和105个导出特征。
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#图片画出所有的训练数据点
plt.plot(X_train, y_train, 'o')
# 得到斜率w和偏置量b
lr = LinearRegression().fit(X_train, y_train)
#输出斜率和偏移量
print('lr.coef_: {}'.format(lr.coef_))
print('lr.intercept_: {}'.format(lr.intercept_))
#由于维度过高,故无法画出其线段
# x = np.arange()
# function_x = lr.coef_[0] * + .......... + lr.intercept_
# plt.plot(x, function_x)
#输出该模型对训练集和测试集的预测准确度
print('train score: {}'.format(lr.score(X_train, y_train))) #测试训练集的预测准确度
print('test score: {}'.format(lr.score(X_test, y_test))) #测试测试集的预测准确度
运行结果
lr.coef_: [-3.71808346e+02 -4.08461267e+01 -9.37633125e+01 -1.70308027e+00
-1.46544003e+01 8.55857260e+01 4.02415779e+01 -6.56057443e+01
2.32423499e+01 2.64870802e+01 2.40635635e+01 2.57962658e+01
7.05095128e+00 1.06046030e+01 2.11046368e+03 1.70960722e+03
1.71040813e+02 -1.20967959e+01 6.66487652e+01 -7.07109856e+00
1.52422392e+01 1.31143774e+03 -2.65114015e+03 3.81919659e+02
-6.04410661e+00 6.30938965e+01 -1.09126785e+01 -3.37705778e+01
-4.85810802e+00 -5.41941690e+01 5.99852178e+00 -1.37968337e+00
-8.70099619e+00 2.86548369e+00 3.56652934e+01 -7.08435449e+00
5.80143510e+01 -1.34335827e+01 4.35450712e+01 1.33121159e+01
-3.53336365e+00 4.24899566e+01 1.52684774e+01 4.59087571e+01
4.82992465e+01 -9.63107615e-01 2.83285925e+00 2.06912891e+01
-2.12035813e+01 -1.70308027e+00 -6.16423766e+00 -2.38588145e+01
5.34418260e+00 3.23314934e+01 1.08011626e+01 -2.16509342e+01
-5.37812177e+00 1.21369092e+01 -1.17281484e+01 1.17692529e+01
7.08138359e+00 -1.25140592e+01 1.33808083e+02 -1.68052136e+01
4.46494172e+01 -5.81364228e+01 8.68875452e-01 1.62005315e+01
2.41691781e+00 -3.49805121e+01 1.56170814e+00 -7.29919268e-01
-5.41743107e+01 -3.31308691e+01 -6.57341451e+00 -3.75952052e+01
2.44180780e-01 -5.91878307e+00 3.86396613e+01 -4.20007555e+01
3.89391775e+00 -2.32674399e+01 -2.70317840e+01 8.32953465e+01
-3.16392277e+01 -4.41416628e+01 -2.84143543e+01 -1.67040303e+01
5.63683861e+01 -1.07091694e+02 9.12885401e+01 -4.45115580e+00
-6.91774176e+00 -3.12052426e+01 -1.93089210e+01 3.01300804e+01
-7.01220172e+00 8.33336850e+00 -5.07060135e+00 1.13641907e+01
-2.14350684e+00 -6.01727670e+00 -4.31583395e+00 2.60989039e+01]
lr.intercept_: -16.554636706891607
train score: 0.9284932305183793
test score: 0.8737520463341264
这次预测训练集和测试集的结果较好,可见,当特征较多时,使用线性回归方法可行。
若出现,训练集预测结果和测试集预测结果差异较大,即出现了过拟合的情况,需要以下两种新的模型解决。
岭回归(Ridge)
岭回归Ridge,该模型的核心是通过正则化的方法,促使每个特征的系数 w 趋向于 0 ,从而避免出现过拟合的情况,即训练集预测结果与测试集预测结果相差较大,考虑了过多或夸大的特征影响,导致了测试集的预测不精确,影响训练集向测试集的泛化。
岭回归Ridge使用参数 alpha 用来控制正则化的强弱。alpha越大,特征系数w就越趋向于0,反之亦然。此种方式被称为L2正则化,Lasso回归被称为L1正则化,我也不懂,有兴趣的朋友可以多做查阅。
sklearn.linear_model 中的 Ridge 类实现了该模型,以下是对该模型的应用测试。
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的房价信息数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#使用Ridge模型训练波士顿房价信息数据集
ridge = Ridge().fit(X_train, y_train)
print('train score: {}'.format(ridge.score(X_train, y_train))) #预测训练集的准确度
print('test score: {}'.format(ridge.score(X_test, y_test))) #预测测试集的准确度
运行结果
train score: 0.8556248260287591
test score: 0.8605931411425929
此时发现,训练集与测试集的预测结果相近,属于欠拟合的情况,即特征数较少的情况,即特征系数w接近0的情况,属于过度正则。我们可以适当缩减alpha,从而减少正则,增加特征的影响,再次测试。
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的房价信息数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#默认alpha为1,调整为0.1,减少正则影响
ridge = Ridge(alpha=0.1).fit(X_train, y_train)
print('train score: {}'.format(ridge.score(X_train, y_train))) #预测训练集的准确度
print('test score: {}'.format(ridge.score(X_test, y_test))) #预测测试集的准确度
运行结果
train score: 0.8953944927234415
test score: 0.9204136280805639
可见,训练集与测试集的预测准确度有所提升,但是再对alpha进行调小,可能会由于特征系数变大、斜率变大造成过拟合,从而造成训练集的预测结果高,测试集的预测结果低,出现不泛化的现象。
Lasso回归
Lasso回归与Ridge回归较为相似,也是采用正则化的方式,控制特征系数w,从而达到泛化稳定效果,不过Lasso采用正则化L1的方法。
与Ridge不同的是,应用情景若仅有几条重要特征时,使用Lasso较为可能更好,更容易理解。
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的房价信息数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#默认alpha为1
lasso = Lasso().fit(X_train, y_train)
print('train score: {}'.format(lasso.score(X_train, y_train))) #预测训练集的准确度
print('test score: {}'.format(lasso.score(X_test, y_test))) #预测测试集的准确度
print('feature num: {}'.format(np.sum(lasso.coef_ != 0))) #Lasso模型特征系数不为0个数
运行结果
train score: 0.2609501463003341
test score: 0.22914497616007956
feature num: 3
可以看出,Lasso在训练集与测试集的预测结果都比较差劲,105个特征仅用到了3个,正则化过于严重,对alpha参数进行调整,减少约束,可得
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的房价信息数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#默认alpha为1,调整为0.001,减少正则影响,并增大迭代最大次数
lasso = Lasso(alpha=0.001, max_iter=100000).fit(X_train, y_train)
print('train score: {}'.format(lasso.score(X_train, y_train))) #预测训练集的准确度
print('test score: {}'.format(lasso.score(X_test, y_test))) #预测测试集的准确度
print('feature num: {}'.format(np.sum(lasso.coef_ != 0))) #Lasso模型特征系数不为0个数
运行结果
train score: 0.9126076194281942
test score: 0.9174465452887482
feature num: 73
训练集和测试集的预测结果均有了明显提升,且用到的特征系数也有73个。
假设再次缩减正则的影响:
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
#生成506个样本和105个导出特征的房价信息数据集
X, y = mglearn.datasets.load_extended_boston()
#将数据集拆分为 训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
#默认alpha为1,调整为0.0001,减少正则影响,并增大迭代最大次数
lasso = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print('train score: {}'.format(lasso.score(X_train, y_train))) #预测训练集的准确度
print('test score: {}'.format(lasso.score(X_test, y_test))) #预测测试集的准确度
print('feature num: {}'.format(np.sum(lasso.coef_ != 0))) #Lasso模型特征系数不为0个数
运行结果
train score: 0.9439155470053099
test score: 0.8116708246332489
feature num: 91
可见,训练集与测试集的预测结果有了明显差异,是过拟合的特征,表示特征系数影响较大,需要再次调高alpha值加强正则化,减少特征系数影响,缩小训练集与测试集的预测结果差异,增强泛化效果。
分类问题的线性模型
线性模型也可以用于分类问题,可以使用以下的公式进行预测:
y = w [ 0 ] ∗ x [ 0 ] + w [ 1 ] ∗ x [ 1 ] + w [ 2 ] ∗ x [ 2 ] + . . . + w [ p ] ∗ x [ p ] + b > 0 y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[p]*x[p] + b > 0 y=w[0]∗x[0]+w[1]∗x[1]+w[2]∗x[2]+...+w[p]∗x[p]+b>0
该公式看起来与线性回归公式十分类似,但并未返回特征的加权求和,而是为预测设置了阈值(0)。
对于回归的线性模型,输出的y是特征的线性函数,是直线、平面、超平面等。
对于分类的线性模型,决策边界是输入的线性函数。换句话说,线性分类器是利用直线、平面、超平面来分开两个或多个类别的分类器。
目前较为常见的两种线性分类算法是 Logistic回归(logistic regression) 和 线性支持向量机(linear support vector machine, 线性SVM)。
LogisticRegression
将 Logistic回归 应用到 forge 数据集上, 并将线性模型找到的决策边界可视化。
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
import mglearn
# 生成 forge 数据集
X, y = mglearn.datasets.make_forge()
#Logistic 回归模型,训练数据,默认参数 C取值为 1
logistic_regression = LogisticRegression(C=1).fit(X, y)
#绘制分界线
mglearn.plots.plot_2d_separator(logistic_regression, X, fill=False, eps=0.5)
#画出所有的数据点及类型
mglearn.discrete_scatter(X[:,0], X[:,1], y)
plt.xlabel('feature01')
plt.ylabel('feature02')
plt.legend()
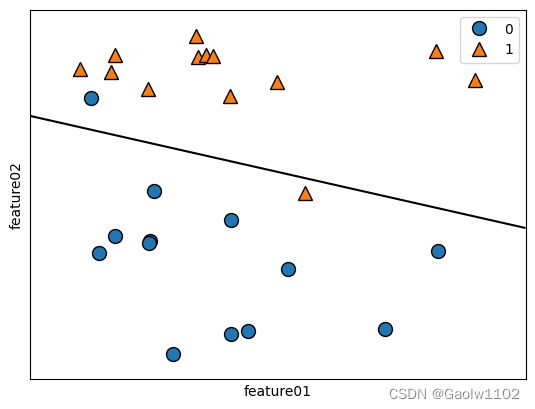
由上图可知,在该线段上方的数据将被预测为 1, 线段下方数据将被预测为 0。
当我们修改 LogisticRegression 的参数C时,该模型会做正则化调整,类似于线性回归模型Ridge和Lasso。
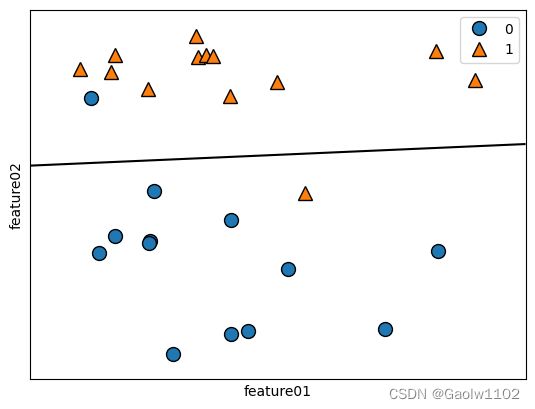
- C = 0.1时
可以观测得出,当C越小时, 正则化越强,该模型越稳定,泛化能力也越强。
看到的朋友可以根据具体场景具体分析,从而敲定参数C的取值。
LinearSVC – 线性支持向量机
将 LinearSVC 与 Logistic回归类似,同样可以用于分类的线性模型,将其应用到 forge 数据集上, 并将线性模型找到的决策边界可视化。
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import numpy as np
import mglearn
# 生成 forge 数据集
X, y = mglearn.datasets.make_forge()
#LinearSVC 回归模型,训练数据,默认参数 C取值为 1
linear_svc = LinearSVC(C=1).fit(X, y)
#绘制分界线
mglearn.plots.plot_2d_separator(linear_svc, X, fill=False, eps=0.5)
#画出所有的数据点及类型
mglearn.discrete_scatter(X[:,0], X[:,1], y)
plt.xlabel('feature01')
plt.ylabel('feature02')
plt.legend()
同理,在该线段上方的数据将被预测为 1, 线段下方数据将被预测为 0。
当我们修改 LinearSVC 的参数C时,该模型也会做正则化调整,Logistic回归 与 LinearSVC 模型均使用L2进行正则化,类似于线性回归模型Ridge和Lasso。
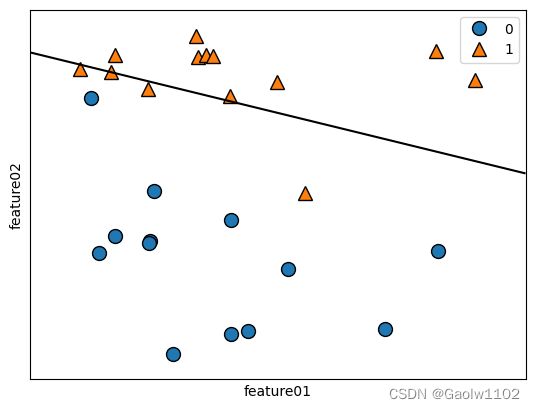
- C = 100 时
- C = 1 时
同样的,对于 LinearSVC 模型,不同参数C的设定同样对预测结果存在影响,在实际应用中,具体的情景可根据测试集最优预测结果来敲定参数C。
总结
线性模型训练速度非常快,预测速度也非常快。
在具体应用中,根据业务场景选择使用 L1正则化的模型(Lasso) 或者 L2正则化的模型(Ridge、Logistic回归、LinearSVC)。