深度学习理论篇
目录
- 传统神经网络nn整体
-
- nn总结
- 前向传播
-
- 像素点参数预处理(input)
- 权重参数初始化
- 得分函数(W * x)
- 激活函数(f(x))
- 分类问题
- 反向传播(更新W)
-
- 损失函数(output和target比较)
- 卷积神经网络CNN
-
- CNN总结
- 卷积层
- 非线性激活
-
- 常用激活函数
-
- Sigmoid
- tanh
- relu
- ELU
- 池化层
- 全连接层
- VGG卷积神经网络
- 残差网络Resnet
-
- 原理
- 注意
- 网络结构
传统神经网络nn整体
nn总结
第一列是图片的三维(列)原始特征,第二列和第三列为特征提取(乘权重、激活等)后,计算机可以看的懂得四维特征。

圆圈: 表示的是特征,是像素点,也是神经元,有几个圈,就证明输入数据有几个特征。
线: 表示乘上权重w、非线性激活等特征提取的工作。乘完权重后,后面紧跟着非线性激活函数。我们希望更新权重时,权重值的波动是比较稳定的,而不是大起大落。
神经元的个数越多(权重参数越多),过拟合风险越大,可通过 dropout机制 和 正则化 来解决:
对于 正则化,其中λ称为正则化参数,当参数越大,则对其惩罚(规范)的力度也就越大,越能起到规范的作用。但是要注意, 并不是越大越好,如果选择的正则化参数过大,则会把所有的参数都最小化了,造成欠拟合。因此,我们对λ的选取需要合理即可。
对于 drop_out,训练时,每层随机杀死部分神经元
前向传播

前向传播的过程:一堆像素点 * 每个像素点的权重+偏差 得到这个分类的得分,再通过得分值和损失函数计算损失,神经元的个数越多,效果越好,但是会有 过拟合 的风险,所以要适当选择神经元个数,可以采用drop-out机制或者加上正则化。
像素点参数预处理(input)
将输入图片的像素点进行预处理
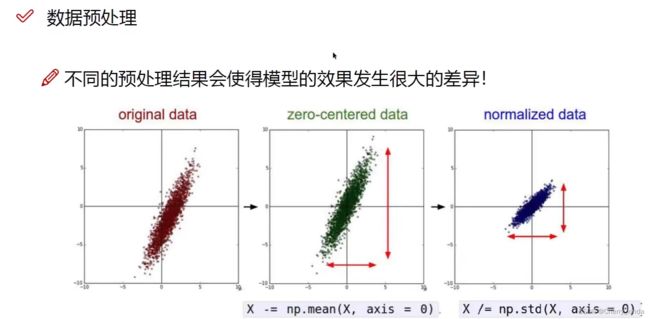
预处理之后,得到输入层 input layer
权重参数初始化
为神经网络分配初始权重,通常采用随机策略(或者训练好的其他模型的权重参数)
得分函数(W * x)

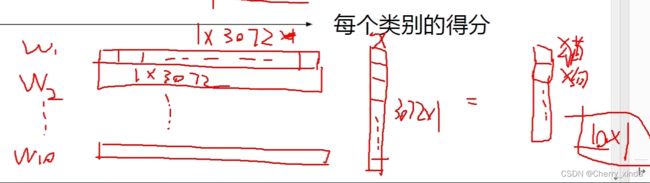
猫的图片共有 32 * 32 * 3=3072 个像素点,每个像素点为一个神经元。
x:代表图片中的像素参数,为 3072 行1列 的矩阵,它是固定不变的。
W:为权重参数,如果有1个分类,那它就为 1行3072列 的矩阵,这样可以保证每个像素点参数都可以乘上对应权重。(图中为10类,则为 10行3072列 的矩阵,W * x 的最终结果为 10行1列 的矩阵)
b:代表偏差,如果有1个分类,则b为一个数。(图中为10类,则b为10行一列的矩阵)

激活函数(f(x))
每一次乘上权重W进行特征提取后,都可以在后面加上非线性激活函数。
分类问题

图片最下面一块(假设真实分类为 cat):
第一列为计算出在猫这张图片,三个分类的得分值,exp(exp函数特性:波动大)的目的是使得差异化更明显,归一化的目的是得到三个分类的概率,最后将log函数当作损失函数来计算损失(负log函数特性:x越小,损失越大!)
反向传播(更新W)
目的是使得损失变小
我们是通过一开始初始化的 权重W * 输入的像素点矩阵 来得到得分,进而通过损失函数(预测值和真实值比较公式)来得到损失的,我们为了使得损失变小,我们要调节权重W,在神经网络中会经过很多层,所以会乘很多次不同的权重W,我们要找出哪一个权重W对损失的影响更大,所以我们通过 损失函数 来分别对每一个权重W求偏导,哪一个导数大,哪一个影响的就更大。我们就可以用权重更新的公式优先对影响更大的进行权重更新。计算偏导时,从后往前逐层地计算
求得得偏导值就是 梯度。
加法门单元: 均等分配梯度,如z = x + y,z对x和y得偏导都为1,梯度给一样的
max门单元:将梯度给最大的,如z = max(x,y),只有对较大的值的偏导才不为零。
乘法门单元:梯度互换,如z = x * y,对一个变量的偏导是另外一个变量。
损失函数(output和target比较)
我们在运行网络时的目标是提高我们的预测精度并减少误差,从而最大限度地降低损失。我们得到损失之后,要通过反向传播来更新权重W。
如果我将成本函数定义为均方误差,则可以写为:
C= 1/m ∑(y–a)^2
其中m是训练输入的数量,a是预测值,y是该特定示例的实际值,学习过程围绕最小化成本来进行。
如果两个神经网络模型的损失相同,那么是否两个模型都可以用呢?
要看两个模型的W,W正则性好的,效果更好,因为每个像素点上都乘上了有效的参数。
如: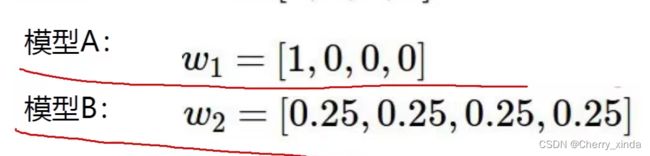 w1容易发生过拟合,所以损失函数最好可以加上正则的比对。
w1容易发生过拟合,所以损失函数最好可以加上正则的比对。
卷积神经网络CNN
CNN总结
输入不再是像素点(二维向量 288 * 1),而是三维图片(如3 * 3 * 32)
直接通过 卷积层提取特征 ,通过 池化层压缩特征。
(卷积、激活、池化、全连接相关知识补充看 五、神经网络)
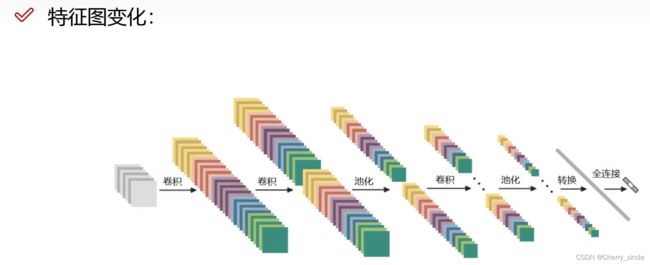
卷积和池化总结:
对于卷积核来说,如果为 3 * 3 的大小,那么该矩阵的元素值为权重w
对于池化核来说,如果为 3 * 3 的大小,该矩阵没有权重参数!
卷积层
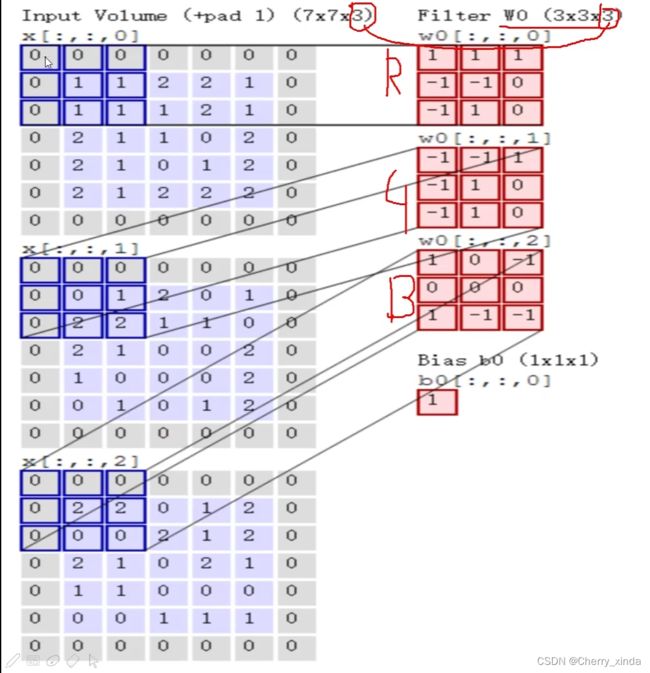
卷积层:将输入图片的三个通道的图像都分别分为n块 ,每一块的大小为卷积核的大小,每一通道中的每一块都会与对应通道的权重矩阵(卷积核)做内积,得到每个通道该块的特征值,再将三个通道该块的特征值相加,再加上偏重,最终得到RGB三通道那一块的最终特征值,依此类推…
三个通道的每一块都乘完后,会得到 单通道 尺寸变小(取决于padding) 的图片,可以通过增加卷积核的个数(每个卷积核的通道数要和输入图片的通道数保持一致),来增加输出图片的通道数,进而增加特征。
此图为一个卷积核,且kener_size(red part)为 3 * 3,input增加了padding,可以增加输入边界值的利用率。
要想得到3通道的特征图output,就要用到3个3通道的卷积核。
非线性激活
常用激活函数
Sigmoid
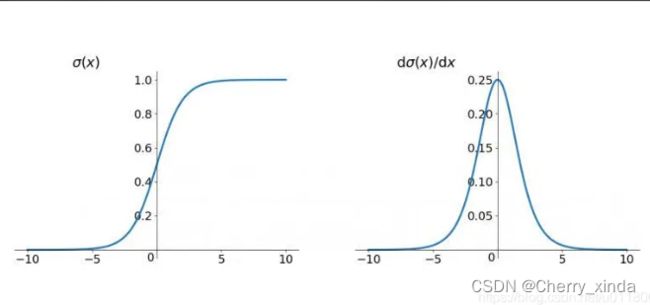
优点:曲线平滑。对称性好。由于导数最大值为0.25,至少不会导致梯度爆炸。
缺点:导数的最大值才0.25,在反馈损失函数的梯度时,如果网络用了多个sigmoid激活函数,在损失函数求链式偏导累乘的过程中,会导致 梯度消失,使得网路收敛缓慢。
tanh
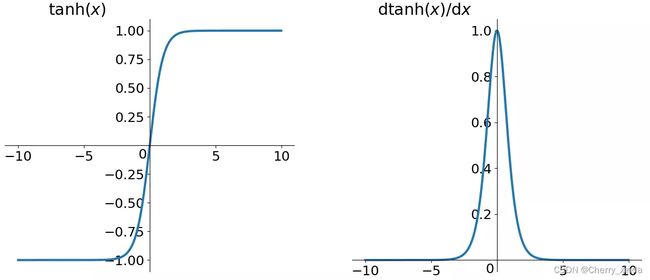
由导数图像可观察,虽然收敛速度要比sigmoid函数快,但是仍然可能导致梯度消失。
relu
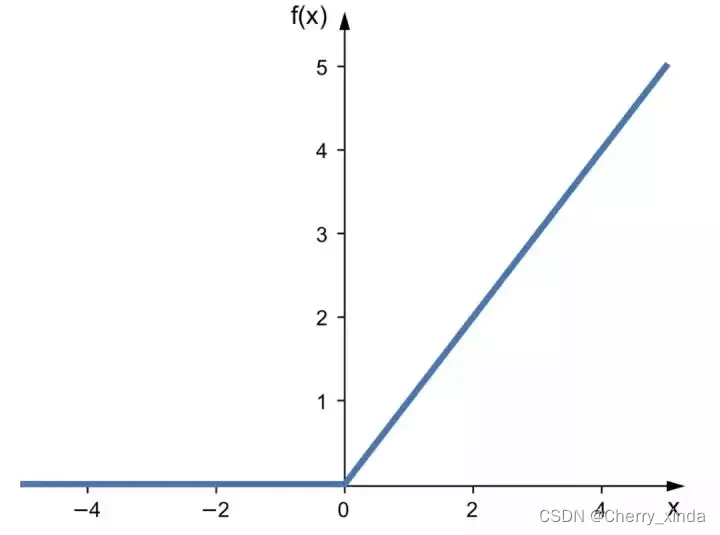
优点:
可有效避免梯度消失和梯度爆炸。
使得网络收敛速度加快。
缺点:
当输入小于0时后,函数值和函数梯度恒为0,导致神经元死亡,权重无法更新。
(关于死亡问题,看收藏内容)
ELU
改进了ReLU函数输入小于0的情况。
相比于ReLU函数,在输入为负数的情况下,具有0到-1的平滑输出。这样可以消除ReLU死掉的问题,但是还是有类似sigmoid函数梯度消失的问题。
池化层
池化层只做特征压缩,没有权重矩阵!

stride默认为池化核的大小kener_size,经过池化层会使得尺寸变小,但是不会改变通道数
分为平均池化和最大池化,经验证,最大池化效果最好。
全连接层
经过卷积层、非线性激活、池化层反复特征提取后,得到的图是一个多维的特征图,无法进行分类任务。
所以要先将该多通道特征图进行展平,得到1行n列的 特征行向量,只有该向量才可以接全连接层。
假定展平后的 特征行向量 为1行32* 32 *10 列,且要进行5类的分类任务。那么就要再经过全连接层,设置in_feature = 10240 ,out_feature = 5
VGG卷积神经网络
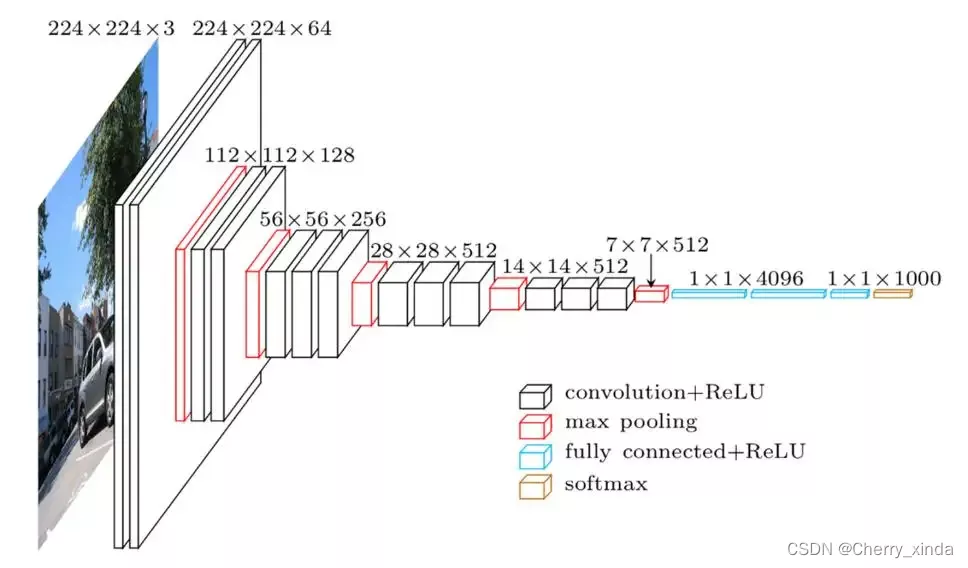
有16层,19层的版本等等,层数不能再多了,否则会造成网络退化!
残差网络Resnet
对于Resnet,层数越多,效果越好。
原理

设计残差网络的目的是因为,当神经网络层数越来越多时,训练集的误差和测试集的误差都越来越大,进而导致神经网络退化,所以产生了Resnet残差网络。
注意
此现象是网络退化,而不是过拟合和梯度消失。
过拟合:训练集训练的时候误差很小,但是测试集测试的时候误差很大。
梯度消失:指的是损失函数没有梯度,说明损失值没有变化。
网络结构

如上图为一个残差块,设H(x) = F(x) + x 。对于线性网络来说,应该是拟合H(x),但是对于残差网络,是拟合F(x) ,也就是残差。
所以说最坏的打算是F(x)为0,没有任何进步,H(x) 为x,但是也不会导致网络退化。
本文笔记整理部分来源于bilibili视频:
https://www.bilibili.com/video/BV1K94y1Z7wn?p=1&vd_source=113e6784e64070309a4cd10c8c8d0c90
残差网络部分笔记来源于bilibili视频:
https://www.bilibili.com/video/BV1vb4y1k7BV?spm_id_from=333.337.search-card.all.click&vd_source=113e6784e64070309a4cd10c8c8d0c90