CART算法
CART算法
CART决策树的生成就是递归的构建二叉决策树的过程。
CART用基尼(Gini)系数最小化准则来进行特征选择,生成二叉树。
Gini系数计算:
G i n i ( D ) = 1 − ∑ i = 1 m p i 2 Gini(D) = 1-\sum_{i=1}^{m}p_i^2 Gini(D)=1−i=1∑mpi2
G i n i A ( D ) = ∣ D 1 ∣ ∣ D ∣ G i n i ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ G i n i ( D 2 ) Gini_A(D) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2) GiniA(D)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)
Δ G i n i ( A ) = G i n i ( D ) − G i n i A ( D ) \Delta Gini(A) = Gini(D) - Gini_A(D) ΔGini(A)=Gini(D)−GiniA(D)
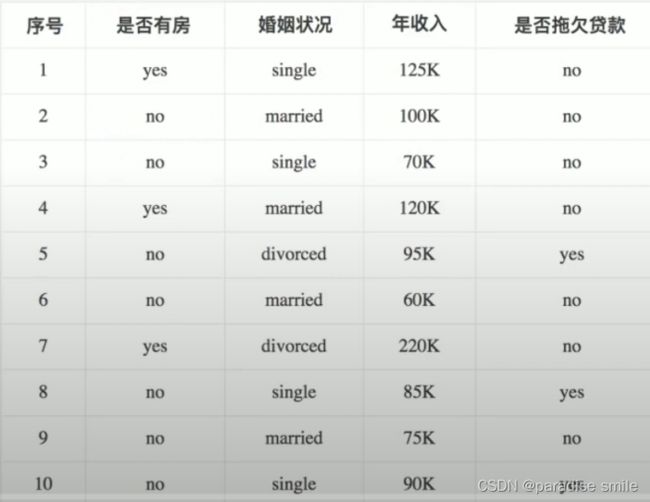
CART举例
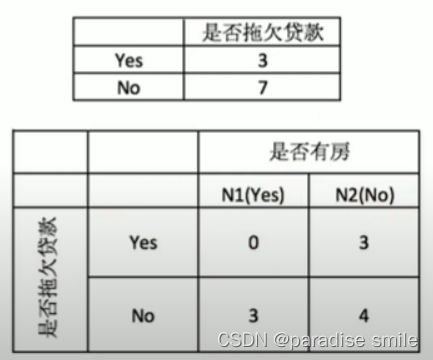
分别计算他们的Gini系数增益,取Gini系数增益值最大的属性作为决策树的根结点属性。根结点的Gini系数:
G i n i ( 是否拖欠贷款 ) = 1 − ( 3 10 ) 2 − ( 7 10 ) 2 = 0.42 Gini(是否拖欠贷款) = 1-(\frac{3}{10})^2-(\frac{7}{10})^2=0.42 Gini(是否拖欠贷款)=1−(103)2−(107)2=0.42
根据是否有房来进行划分时,Gini系数增益计算:左节点代表yes,右节点代表no
G i n i ( 左子节点 ) = 1 − ( 0 3 ) 2 − ( 3 3 ) 2 = 0 G i n i ( 右子节点 ) = 1 − ( 3 7 ) 2 − ( 4 7 ) 2 = 0.4898 Gini(左子节点) = 1-(\frac{0}{3})^2 -(\frac{3}{3})^2 = 0 \\ Gini(右子节点) = 1-(\frac{3}{7})^2-(\frac{4}{7})^2 = 0.4898 Gini(左子节点)=1−(30)2−(33)2=0Gini(右子节点)=1−(73)2−(74)2=0.4898
Δ ( 是否有房 ) = 0.42 − 3 10 ⋅ 0 − 7 10 ⋅ 0.4898 = 0.077 \Delta(是否有房) = 0.42 - \frac{3}{10} \cdot 0 - \frac{7}{10}\cdot 0.4898 = 0.077 Δ(是否有房)=0.42−103⋅0−107⋅0.4898=0.077
根据婚姻状况来进行划分时,Gini系数增益计算:
-{married}|{single, divorced}
-{sigle}|{married, divorced}
-{divorced}|{single, married}
当分组为{married}|{single, divorced}时:
Δ ( 婚姻状况 ) = 0.42 − 4 10 ( 1 − 1 2 ) − 6 10 ( 1 − ( 3 6 ) 2 − ( 3 6 ) 2 ) = 0.12 \Delta (婚姻状况) = 0.42 - \frac{4}{10}(1 - 1^2) - \frac{6}{10}(1-(\frac{3}{6})^2-(\frac{3}{6})^2) = 0.12 Δ(婚姻状况)=0.42−104(1−12)−106(1−(63)2−(63)2)=0.12
当分组为{single}|{married, divorced}时:
Δ ( 婚姻状况 ) = 0.42 − 4 10 ( 1 − ( 1 2 ) 2 − ( 1 2 ) 2 ) − 6 10 ( 1 − ( 5 6 ) 2 − ( 1 6 ) 2 ) = 0.053 \Delta(婚姻状况) = 0.42 - \frac{4}{10}(1-(\frac{1}{2})^2-(\frac{1}{2})^2) - \frac{6}{10}(1-(\frac{5}{6})^2-(\frac{1}{6})^2) = 0.053 Δ(婚姻状况)=0.42−104(1−(21)2−(21)2)−106(1−(65)2−(61)2)=0.053
当分组为{divorced}|{single, married}时:
Δ ( 婚姻状况 ) = 0.42 − 2 10 ( 1 − ( 1 2 ) 2 − ( 1 2 ) 2 ) − 8 10 ( 1 − ( 6 8 ) 2 − ( 2 8 ) 2 ) = 0.02 \Delta(婚姻状况) = 0.42 - \frac{2}{10}(1-(\frac{1}{2})^2-(\frac{1}{2})^2) - \frac{8}{10}(1-(\frac{6}{8})^2-(\frac{2}{8})^2) = 0.02 Δ(婚姻状况)=0.42−102(1−(21)2−(21)2)−108(1−(86)2−(82)2)=0.02
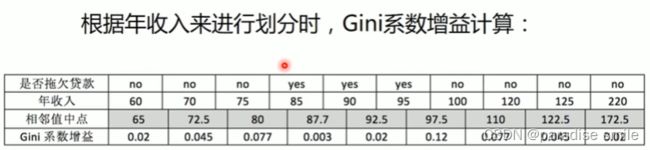
例如当面对年收入为60和70这两个值时,我们算得其中间值为65,倘若以中间值65作为分割点,于是则得Gini系数增益为:
0.42 − 1 10 ( 1 − 1 2 ) − 9 10 ( 1 − ( 6 9 ) 2 − ( 3 9 ) 2 ) = 0.02 0.42 - \frac{1}{10}(1-1^2) - \frac{9}{10}(1-(\frac{6}{9})^2-(\frac{3}{9})^2) = 0.02 0.42−101(1−12)−109(1−(96)2−(93)2)=0.02
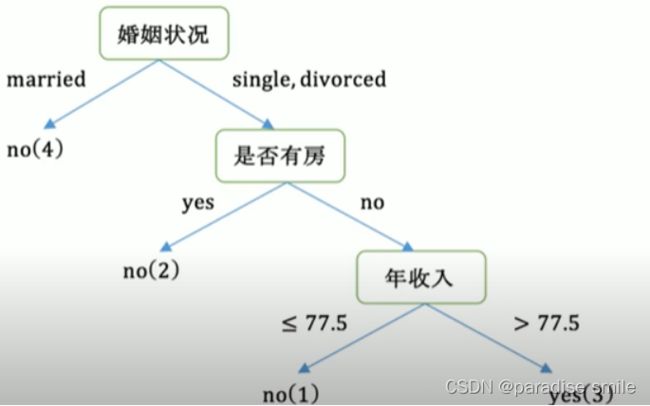
根据计算知道,三个属性划分根节点的增益最大的有两个:年收入属性和婚姻状况,他们的增益都是0.12.可以随机选择一个作为根节点。假如我们选择婚姻状况作为根节点。接下来,使用同样的方法,分别计算剩下的属性,其中根节点的Gini系数为:
G i n i ( 是否拖欠贷款 ) = 1 − ( 3 6 ) 2 − ( 3 6 ) 2 = 0.5 Gini(是否拖欠贷款) = 1-(\frac{3}{6})^2-(\frac{3}{6})^2=0.5 Gini(是否拖欠贷款)=1−(63)2−(63)2=0.5
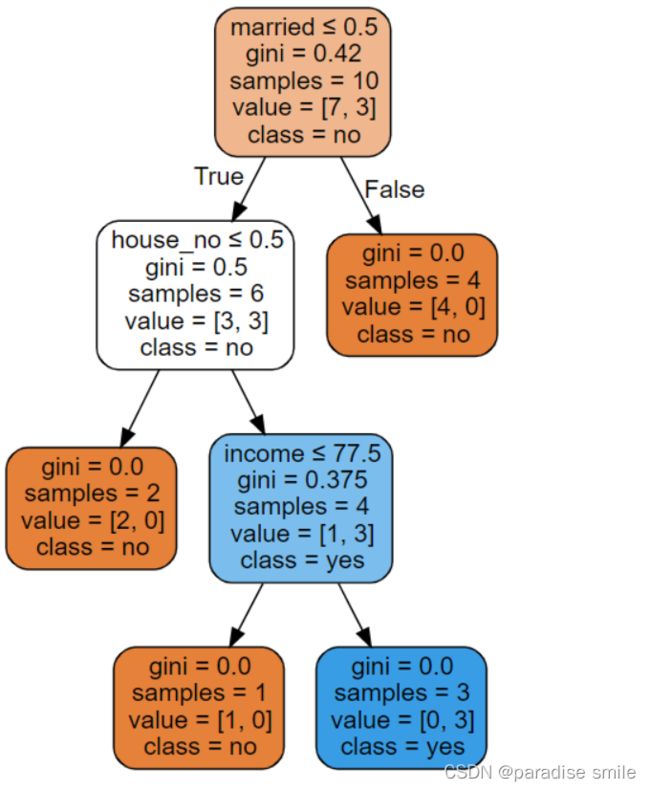
最后构建的CART
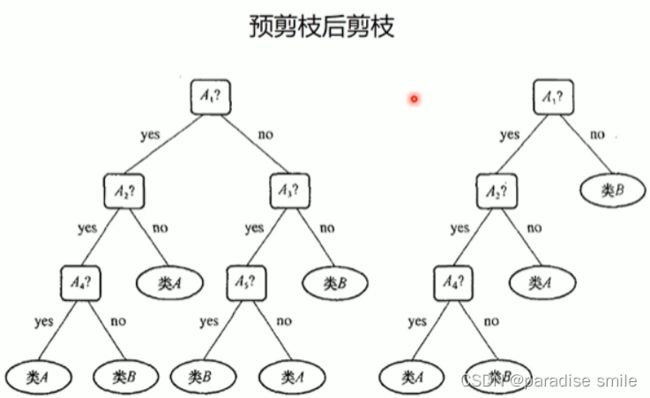
剪枝
优缺点
优点:小规模数据集有效
缺点:1.处理连续变量不好 2.类别较多时,错误增加的比较快 3.不能处理大量数据
示例
from sklearn import tree
import numpy as np
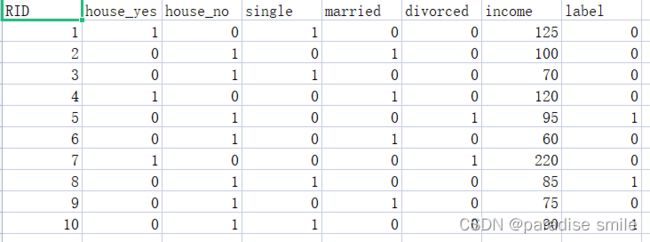
#载入数据
data = np.genfromtxt('cart.csv', delimiter=',')
x_data = data[1:, 1:-1]
y_data = data[1:, -1]
# 创建决策树模型
model = tree.DecisionTreeClassifier()
#输入数据建立模型
model.fit(x_data, y_data)
import graphviz
dot_data = tree.export_graphviz(model, out_file=None,
feature_names=['house_yes', 'house_no', 'single', 'married', 'divorced', 'income'],
class_names = ['no', 'yes'],
rounded = True,
filled=True,
special_characters=True
)
graph = graphviz.Source(dot_data)
graph.render('cart')
graph