机器学习（五）模型评估与优化

目录

一、定义和公式

1. 过拟合Overfit与欠拟合Underfit

2. 数据分离与混淆矩阵 Confusion Matrix

3. 模型优化

二、 代码实战

1. 酶活性预测

1.1 建立线性回归模型，计算测试数据集上的R2分数，可视化

1.2 加入多项式特征（2次，5次）建立回归模型，用R2分数对比两个模型预测结果

1.3 可视化多项式回归模型，对比两个模型预测结果

2. 芯片质量好坏预测

2.1 根据高斯分布概率密度函数，寻找异常点并剔除

2.2 基于data_class_processed.csv数据，进行PCA处理，确定重要数据维度及成分

2.3 调用sklearn库，根据数据分离参数完成训练与测试数据分离

2.4 建立KNN模型完成分类，计算准确率，可视化分类边界

2.5 计算测试数据集对应的混淆矩阵，计算准确率、召回率、特异度、精确率、F1分数

2.6 尝试不同的n_neighbors，计算其在训练数据集、测试数据集上的准确率并可视化

---

一、定义和公式

1. 过拟合Overfit与欠拟合Underfit

由于模型不合适，无法对新数据实现有效预测

过拟合原因：

1. 模型结构过于复杂，维度过高
2. 属性太多，模型训练时包含了干扰项信息

过拟合解决：

1. 简化模型结构，用低阶模型，如线性模型
2. 数据预处理，保留主成分信息，如PCA
3. 训练时，增加正则项 Regularization

正则化处理：

通过引入正则化，lambda取值大的情况下，可约束限制theta的取值，从而限制各个属性(高次项theta)数据的影响，从而使边界函数平滑

原线性回归损失函数：

正则化处理后的损失函数：

 

当lambda尽可能大时，theta系数之和缩小，也就是让lambda去控制theta的取值范围，从而让损失函数更小

---

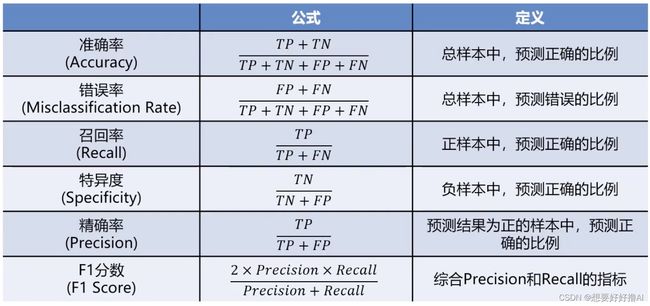
2. 数据分离与混淆矩阵 Confusion Matrix

准确率Accuracy评估方法的局限：无法反映模型对各个分类的预测准确度，只有总样本数，没有每个样本的分布

混淆矩阵：误差矩阵，用于衡量分类算法的准确程度

记忆方法：

第一个字母T/F：判断预测是否准确，模型预测与实际一致时为T，不一致为F

第二个字母P/N：记录模型预测的结果，模型预测是什么就是什么

通过混淆矩阵，更多评估指标：

 例：0-1预测

实际：900个1，100个0，预测：1000个1，0个0，假设负样本为0，正样本为1，通过计算得出：TN=0，FP=100，FN=0，TP=900，将其代入公式计算出各个评估指标 

---

3. 模型优化

为什么要模型优化？

问题1：给定一个新任务，应该用什么算法？

如一个二分类任务，有4种算法：逻辑回归，KNN，决策树，神经网络

问题2：具体算法的核心结构或参数该如何选择？

如逻辑回归的边界函数用线性还是多项式？KNN的核心参数n_neighbors取多少合适？

问题3：模型表现不佳怎么办？

如训练数据准确率低，欠拟合；测试数据准确率下降明显，过拟合；召回率/特异度/精确率低

数据质量的重要性：

1. 数据属性的意义(是否为无关数据)---->删除不必要的数据，减少过拟合，节约时间
2. 不同属性数据的数量级差异性如何(x和y轴数据比例大)---->预处理：归一化/标准化，平衡数据影响，加快训练收敛
3. 是否有异常数据(可视化或异常检测方法)---->过滤异常数据，提高鲁棒性
4. 采集数据的方法是否合理，采集到的数据是否具有代表性(是否长期适用)---->尝试不同模型并对比，确定更合适的模型
5. 要确保标签判定规则的一致性(标签不能总变)

模型优化方法：

1. 数据：异常数据处理，数据量级差异归一化/标准化，扩大数据样本，加/减数据属性，降维PCA处理
2. 核心参数：各个参数组合，如尝试不同n_neighbors的值，逻辑回归多项式(1次，2次...)
3. 正则化：调整lambda的值，去约束theta的取值范围，控制它的影响

---

二、 代码实战

1. 酶活性预测

# 1. load the data
import pandas as pd
import numpy as np
data_train = pd.read_csv('T-R-train.csv')
data_train

# 2. define X_train and y_train
X_train = data_train.loc[:,'T']
y_train = data_train.loc[:,'rate']

# 3. visualize the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(5,5))
plt.scatter(X_train,y_train)
plt.title('raw data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()

# 4. 维度转换
X_train = np.array(X_train).reshape(-1,1)

fig1:

---

1.1 建立线性回归模型，计算测试数据集上的R2分数，可视化

'''
任务1：基于T-R-train.csv数据，建立线性回归模型，计算其在T-R-test.csv数据上的R2分数，可视化模型预测结果 
'''
# 5. linear regression model prediction
from sklearn.linear_model import  LinearRegression
lr1 = LinearRegression()
lr1.fit(X_train,y_train)

# 6. load the test data
data_test = pd.read_csv('T-R-test.csv')
X_test = data_test.loc[:,'T']
y_test = data_test.loc[:,'rate']

# 7. 维度转换
X_test = np.array(X_test).reshape(-1,1)

# 8. 在训练和测试数据上做预测，并计算R2分数
# make prediction on the training and testing data
y_train_predict = lr1.predict(X_train)
y_test_predict = lr1.predict(X_test)
from sklearn.metrics import r2_score
r2_train = r2_score(y_train,y_train_predict)
r2_test = r2_score(y_test,y_test_predict)
print('training r2:',r2_train)
print('test r2:',r2_test)

# 9. 生成新数据并预测 generate new data
X_range = np.linspace(40,90,300).reshape(-1,1)
y_range_predict = lr1.predict(X_range)

# 10. 可视化新数据在模型中的预测结果
fig2 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_range_predict)
plt.scatter(X_train,y_train)

plt.title('prediction data')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()

fig2:

---

1.2 加入多项式特征（2次，5次）建立回归模型，用R2分数对比两个模型预测结果

'''
任务2：加入多项式特征（2次、5次），建立回归模型，计算多项式回归模型对测试数据进行预测的R2分数，判断哪个模型预测更准确
'''
# 5. 生成新属性：2次和5次    generate new features
from sklearn.preprocessing import PolynomialFeatures
poly2 = PolynomialFeatures(degree=2)
X_2_train = poly2.fit_transform(X_train)
X_2_test = poly2.transform(X_test)

poly5 = PolynomialFeatures(degree=5)
X_5_train = poly5.fit_transform(X_train)
X_5_test = poly5.transform(X_test)

print(X_2_train.shape)
print(X_5_train.shape)

# 6. 分别创建2次和5次多项式的实例，训练模型，预测模型
lr2 = LinearRegression()
lr2.fit(X_2_train,y_train)

y_2_train_predict = lr2.predict(X_2_train)
y_2_test_predict = lr2.predict(X_2_test)
r2_2_train = r2_score(y_train,y_2_train_predict)
r2_2_test = r2_score(y_test,y_2_test_predict)

lr5 = LinearRegression()
lr5.fit(X_5_train,y_train)

y_5_train_predict = lr5.predict(X_5_train)
y_5_test_predict = lr5.predict(X_5_test)
r2_5_train = r2_score(y_train,y_5_train_predict)
r2_5_test = r2_score(y_test,y_5_test_predict)

print('training r2_2:',r2_2_train)
print('test r2_2:',r2_2_test)
print('training r2_5:',r2_5_train)
print('test r2_5:',r2_5_test)
'''
结果：
training r2_2: 0.9700515400689422
test r2_2: 0.9963954556468684
training r2_5: 0.9978527267187657 ----> 过拟合，训练好，测试不好
test r2_5: 0.5437837627381457 ----> 准确率低，预测不准确
总结：2次多项式回归模型效果更好
'''

---

1.3 可视化多项式回归模型，对比两个模型预测结果

'''
任务3：可视化多项式回归模型数据预测结果，判断哪个模型预测更准确
'''
# 7. 使用linspace方法创建等差数列
X_2_range = np.linspace(40,90,300).reshape(-1,1)
X_2_range = poly2.transform(X_2_range)
y_2_range_predict = lr2.predict(X_2_range)

X_5_range = np.linspace(40,90,300).reshape(-1,1)
X_5_range = poly5.transform(X_5_range)
y_5_range_predict = lr5.predict(X_5_range)

# 8. 可视化2次多项式实际与预测结果
fig3 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_2_range_predict)
plt.scatter(X_train,y_train)
plt.scatter(X_test,y_test)

plt.title('polynomial prediction result (2)')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()

# 9. 可视化5次多项式实际与预测结果
fig4 = plt.figure(figsize=(5,5))
plt.plot(X_range,y_5_range_predict)
plt.scatter(X_train,y_train)
plt.scatter(X_test,y_test)

plt.title('polynomial prediction result (5)')
plt.xlabel('temperature')
plt.ylabel('rate')
plt.show()

'''
5次多项式回归模型过拟合，2次多项式效果最好
'''

fig3:

fig4:

 

---

2. 芯片质量好坏预测

2.1 根据高斯分布概率密度函数，寻找异常点并剔除

'''
任务1：基于data_class_raw.csv数据，根据高斯分布概率密度函数，寻找异常点并剔除
'''
# 1. load the data
import pandas as pd
import numpy as np
data = pd.read_csv('data_class_raw.csv')
data.head()

# 2. define X and y
X = data.drop(['y'],axis=1)
y = data.loc[:,'y']

# 3. visualize the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(5,5))
bad = plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
plt.legend((good,bad),('good','bad'))
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

# 4. 异常检测 anomay detection
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.02)
ad_model.fit(X[y==0])
y_predict_bad = ad_model.predict(X[y==0])
print(y_predict_bad)

# 5. 可视化异常检测点
fig2 = plt.figure(figsize=(5,5))
bad = plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
plt.scatter(X.loc[:,'x1'][y==0][y_predict_bad==-1],X.loc[:,'x2'][y==0][y_predict_bad==-1],marker='x',s=150)
plt.legend((good,bad),('good','bad'))
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

fig1:

 fig2:

---

2.2 基于data_class_processed.csv数据，进行PCA处理，确定重要数据维度及成分

'''
任务2：基于data_class_processed.csv数据，进行PCA处理，确定重要数据维度及成分
'''
# 1. 加载数据
data = pd.read_csv('data_class_processed.csv')
data.head()

# 2. define X and y
X = data.drop(['y'],axis=1)
y = data.loc[:,'y']

# 3. 主成分分析，pca 
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
X_norm = StandardScaler().fit_transform(X)
pca = PCA(n_components=2)  # 保留2个主成分信息，即2维数据集
X_reduced = pca.fit_transform(X_norm)
var_ratio = pca.explained_variance_ratio_
print(var_ratio)
fig3 = plt.figure(figsize=(5,5))
plt.bar([1,2],var_ratio)
plt.show()

fig3:

---

2.3 调用sklearn库，根据数据分离参数完成训练与测试数据分离

'''
任务3：完成数据分离，数据分离参数：random_state=4,test_size=0.4
'''
# train and test split: random_state=4,test_size=0.4
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=4,test_size=0.4)
print(X_train.shape,X_test.shape,X.shape) # (21, 2) (14, 2) (35, 2)

---

2.4 建立KNN模型完成分类，计算准确率，可视化分类边界

'''
任务4：建立KNN模型完成分类，n_neighbors取10，计算分类准确率，可视化分类边界
'''
# 1. knn model
from sklearn.neighbors import KNeighborsClassifier
knn_10 = KNeighborsClassifier(n_neighbors=10)
knn_10.fit(X_train,y_train)
y_train_predict = knn_10.predict(X_train)
y_test_predict = knn_10.predict(X_test)

#calculate the accuracy
from sklearn.metrics import accuracy_score
accuracy_train = accuracy_score(y_train,y_train_predict)
accuracy_test = accuracy_score(y_test,y_test_predict)
print("trianing accuracy:",accuracy_train)
print('testing accuracy:',accuracy_test)

# 2. 生成网格点坐标矩阵
xx, yy = np.meshgrid(np.arange(0,10,0.05),np.arange(0,10,0.05))
print(yy.shape)

# 3. 扁平化操作，返回一个数组
x_range = np.c_[xx.ravel(),yy.ravel()]
print(x_range.shape)

# 4. 模型预测
y_range_predict = knn_10.predict(x_range)

# 5. 可视化KNN模型结果及其边界 visualize the knn result and boundary
fig4 = plt.figure(figsize=(10,10))
knn_bad = plt.scatter(x_range[:,0][y_range_predict==0],x_range[:,1][y_range_predict==0])
knn_good = plt.scatter(x_range[:,0][y_range_predict==1],x_range[:,1][y_range_predict==1])

bad = plt.scatter(X.loc[:,'x1'][y==0],X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1],X.loc[:,'x2'][y==1])
plt.legend((good,bad,knn_good,knn_bad),('good','bad','knn_good','knn_bad'))
plt.title('prediction result')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

fig4:

---

2.5 计算测试数据集对应的混淆矩阵，计算准确率、召回率、特异度、精确率、F1分数

'''
任务5：计算测试数据集对应的混淆矩阵，计算准确率、召回率、特异度、精确率、F1分数
'''
# 1. 导入库，创建混淆矩阵实例
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test,y_test_predict)
print(cm)

# 2. 定义TP，TN，FP，FN
TP = cm[1,1]
TN = cm[0,0]
FP = cm[0,1]
FN = cm[1,0]
print(TP,TN,FP,FN)

# 3. 计算准确率：Accuracy = (TP + TN)/(TP + TN + FP + FN)
accuracy = (TP + TN)/(TP + TN + FP + FN)
print(accuracy)

# 4. 计算召回率（灵敏度）：Sensitivity = Recall = TP/(TP + FN)
recall = TP/(TP + FN)
print(recall)

# 5. 计算特异度：Specificity = TN/(TN + FP)
specificity = TN/(TN + FP)
print(specificity)

# 6. 计算精确度：Precision = TP/(TP + FP)
precision = TP/(TP + FP)
print(precision)

# 7. 计算F1分数：F1 Score = 2*Precision X Recall/(Precision + Recall)
f1 = 2*precision*recall/(precision+recall)
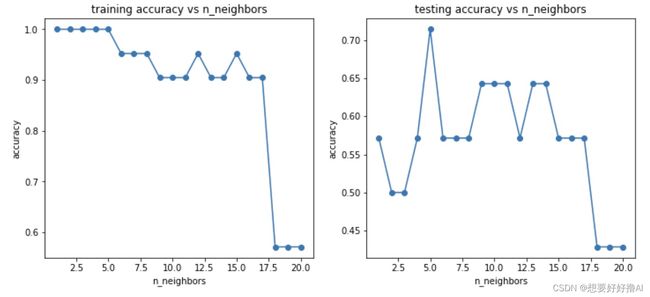
print(f1)

---

2.6 尝试不同的n_neighbors，计算其在训练数据集、测试数据集上的准确率并可视化

'''
任务6：尝试不同的n_neighbors（1-20）,计算其在训练数据集、测试数据集上的准确率并作图
'''
# 1. try different k and calcualte the accuracy for each
n = [i for i in range(1,21)]
accuracy_train = []
accuracy_test = []
for i in n:
    knn = KNeighborsClassifier(n_neighbors=i)
    knn.fit(X_train,y_train)
    y_train_predict = knn.predict(X_train)
    y_test_predict = knn.predict(X_test)
    accuracy_train_i = accuracy_score(y_train,y_train_predict)
    accuracy_test_i = accuracy_score(y_test,y_test_predict)
    accuracy_train.append(accuracy_train_i)
    accuracy_test.append(accuracy_test_i)
print(accuracy_train,accuracy_test)

# 2. 可视化
fig5 = plt.figure(figsize=(12,5))
plt.subplot(121)
plt.plot(n,accuracy_train,marker='o')
plt.title('training accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.ylabel('accuracy')
plt.subplot(122)
plt.plot(n,accuracy_test,marker='o')
plt.title('testing accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.ylabel('accuracy')

plt.show()

fig5: