超分算法之SRCNN

这篇文章是2014年的一篇论文，其主要意义在于作者推出的SRCNN是深度学习在超分上开篇之作！SRCNN证明了深度学习在超分领域的应用可以超越传统的插值等办法取得较高的表现力。

参考目录：
①深度学习图像超分辨率开山之作SRCNN（一）原理分析
②深度学习端到端超分辨率方法发展历程

1 SRCNN简介

1. 作者推出了一种基于SISR的超分方法。这种方法基于深度学习，旨在实现一种端对端的网络模型——SRCNN，其用于将低分辨率的图像转换为高分辨图像。作者指出，SRCNN在当时的数据集下达到了SOAT的水平。

2. SRCNN具有结构简单且低失真度的特点：如上图所示，只需要一定的训练回合，SRCNN就可以超过传统的超分方法。

3. 在一定数量的卷积层结构下，SRCNN可以达到fast-training。

4. 实验表明，在一定范围内，越大的数据集和较大的网络模型可以提升SRCNN对图像的重建效果。

2 SRCNN模型结构

首先说明以下符号的含义：

1. $Y$：输入图像经过预处理(双三次插值)得到的图像，我们仍将$Y$当作是低分辨率图像，但它的size要比输入图像要大。
2. $F(Y)$：网络最后输出的图像，我们的目标就是通过优化$F(Y)$和Ground-Truth之间的loss来学会这个函数$F(\cdot )$。
3. $X$：高分辨率图像，即Ground-Truth，它和$Y$的size是相同的。

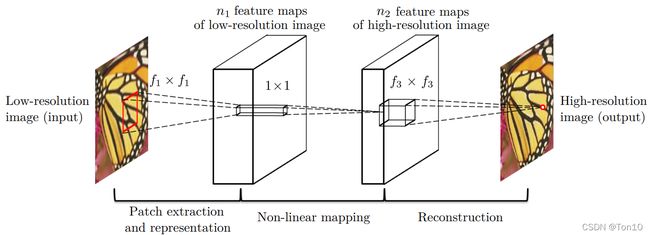
如上图所示是SRCNN的网络模型，其分为三部分，分别是：
①：Patch extraction and representation(其实就是图像特征提取层)。通过CNN将图像$Y$的特征提取出来存到向量中，这个向量里包含了多张feature map，即一张图所含的一些特征。
②：非线性映射层。将上一层的feature map进一步做非线性映射处理，使得网络深度加大，更有利于学到东西。
③：网络重建层。重建用于将feature map进行还原成高分辨率图像$F(Y)$，其与$X$做loss并通过反传来学习整个模型的参数。

下面分别详细展开论述上面三个层。

特征提取层：
特征提取层用了一层的CNN以及ReLU去将图像$Y$变成一堆堆向量，即feature map：
$$F_1(Y)=max(0,W_1\cdot Y+B_1).$$其中$W_1、B_1$是滤波器(卷积核)的参数，这是一个$f_1\times f_1$大小的窗口，通道数为$Y$的通道$c$，一共有$n_1$个滤波器。
Note:

1. 经过这一层，图像$Y$的大小以及通道数都会发生改变。
2. $max(0,x)$表示ReLU层。

非线性映射层：
这一层就是将上一层的feature map再用卷积核过滤一次以及ReLU层进行激活，也可以理解为为了加深网络从而更好的学习函数$F(\cdot )$：
$$F_2(Y)=max(0,W_2\cdot F_1(X)+B_2).$$大致结构和特征提取层一样，不一样的是这一层只是为了增加网络模型的非线性程度，所以只需采用$1\times 1$的卷积核就可以了，其通道数为$n_1$，一共有$n_2$个滤波器。当然可以继续增加非线性层，但是本文旨在推出一种通用性SR框架，所以会选择最简的网络模型。

图像重建层：
借鉴于传统超分的纯插值办法——对图像局部进行平均化的思想，其本质就是乘加结合的方式，因此作者决定采用卷积的方式(也是乘加结合的方式)去做重建：
$$F(Y)=W_3\cdot F_2(Y)+B_3.$$这一层是不需要ReLU层的，且卷积核的大小为$n_2\times c\times f_3\times f_3$.
Note：

1. 也可以从另一个角度来考虑，经过前面的卷积之后，图像的size变小了，因此需要上采样过程来恢复图像，势必需要一个反卷积来做这件事，而反卷积本质也是卷积的一种。

3 Loss function：

设batchsize为$n$，SRCNN网络参数集为$\Theta =\{W_1,W_2,W_3,B_1,B_2,B_3\}$，则Loss function可定义为：
$$L(\Theta )=\frac{1}{n}\sum _{i=1}^n||F(Y_i;\Theta )-X_i|{|}^2.$$Note：

1. 选择MSE作为损失函数的一个重要原因是MSE的格式和我们图像失真评价指标PSNR很像，因此可以理解为SRCNN是直接冲着提升PSNR去的，从而让高分辨率的图像有较小的失真度。
2. MSE就是迫使网络将我们恢复的SR图像向着Ground-Truth(标签$X$)的方向靠近。

4 实验

4.1 setup

实验的一些比较重要的配置如下：

1. Training-data涉及91张图片。Set5数据集涉及5张图片用于up-scale-factor={2,3,4}的验证与测试；Set14数据集涉及14张图片用于up-scale-factor=3的验证与测试。
2. 实验的一些参数设置：$f_1=9,f_3=5,n_1=64,n_2=32$.
3. Ground-Truth的大小是$32\times 32$。
4. 卷积核的参数初始化来自于：$w_i^0\sim \mathcal{N}(0,0.001)$。
5. SRCNN一共3层网络，前两层配置的学习率为$10^{-4}$，最后一层的学习率配置为$10^{-5}$，作者指出这种让最后一层较小的学习率有利于网络收敛。

4.2 实验结果

4.2.1 performance

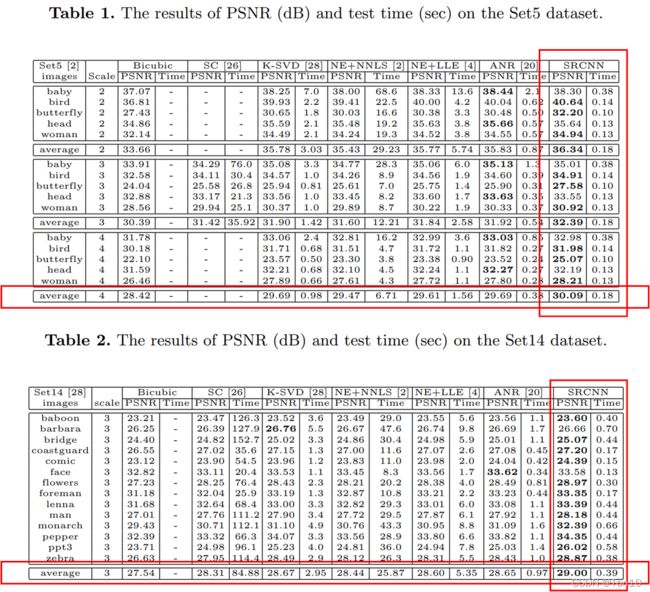从上图看出SRCNN的PSNR在大部分图片中都取得了最佳的值！此外，所消耗的时间也是最少的。

4.2.2 runtime

从上图可以看出SRCNN有最少的runtime！

5 进一步研究

5.1 滤波器学习情况

上图是特征提取层滤波器的学习可视化图，在91张图片的训练结果，其中up-scale-factor=2。
图像a、f：类似于高斯分布。
图像b、c、d：类似于边缘检测。
图像e：类似于纹理检测。
其余：一些坏死的卷积核参数。

5.2 ImageNet学习

作者这一节旨在探究数据集的大小对performance的影响。

1. 采用ILSVRC 2013的ImageNet数据集和91张图片这两个训练集做对比训练。
2. 在Set5数据上做测试，up-scale-factor=3。

实验结果如下：
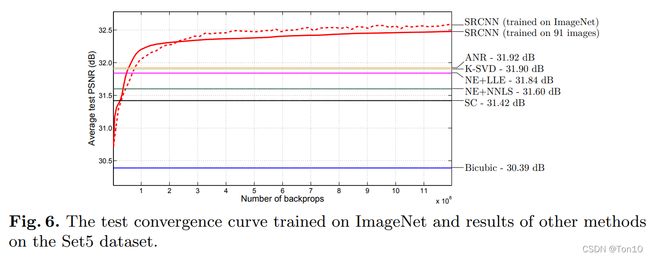从图中可知，大的数据集对表现力的提升是有帮助的(虽然我们都知道，但是作者还是做个实验来证明下)。

5.3 滤波器数量

作者研究滤波器数量对PSNR的提升影响，设置了3组实验，结果如下：

实验结果表明卷积核的数量对表现力是有提升的，但是数量的增加也带来了runtime的增加，如果你想获取快速的重建效果，建议还是取小数量的卷积核更好。

5.4 滤波器大小

作者研究滤波器size对PSNR的提升影响，进行了2组实验，分别是：
$f_1=9,f_3=5$和$f_1=11,f_3=7$。
从实验结果来看，较大的卷积核可以提取更好的特征信息，但是也带来了runtime的上升，因此实际中我们需要根据实际情况进行trade-off。

6 效果展示

7 总结

1. 本文作为SR在深度学习领域的开篇之作，提出了一种通用性框架SRCNN，将输入图像进行Bicubic插值预处理，然后特征提取，非线性映射，最后进行重建；重建后的图像与Ground-Truth做loss来迫使网络学习到如何从$LR\to HR$的知识。
2. 选用深度学习常用的MSE作为Loss function，因为MSE与PSNR有着相似的表达式。
3. SRCNN在PSNR和runtime上都表现不俗，超越了当时的SOAT，表征了这种框架的实用性。
4. 作者做了一系列实验，其中包括可视化乐特征提取到的向量是怎么样的；大的数据集对表现力的提升是有帮助的；卷积核的数量的增加对表现力是有提升的，但是数量的增加也带来了runtime的增加；较大的卷积核可以提取更好的特征信息，但是也带来了runtime的上升。