Python_差分进化算法入门学习_代码例程

目录

前言

基础概念

初始化：

变异：

交叉：

选择：

代码实现

结果展示

 参考资料

---

前言

差分进化算法DE是一种高效的全局优化算法。它也是基于群体的启发式搜索算法，群中的每个个体对应一个解向量。差分进化算法的进化流程则与遗传算法非常类似，都包括变异、杂交和选择操作，但这些操作的具体定义与遗传算法有所不同。这一点格外需要注意，特别是刚从遗传算法过度到差分进化算法的小伙伴。本文会跟大家一起学习，对基础概念进行简单讲解，最后以一个案例作为载体进行代码编写，熟悉差分进化算法。

基础概念

希望大家阅读的时候已经有了基本的遗传算法的知识，这样学习差分进化算法就会快很多，我会尽量详细地介绍差分进化算法，如果实在有疑惑的同学可以参考一下我之前关于遗传算法的几篇博客。进入正文。

差分进化算法操作顺序与遗传算法类似，却有自己的独特之处。下面按顺序进行讲解。

初始化：

可以理解为生成初代种群，但是与遗传算法不同的是，它的每一个个体是实数值参数向量，遗传算法可以是二进制编码，这一点的不同，也间接地暗示了之后在种群进行迭代的时候，遗传算法时采取的变异和交叉的方式，不再适用于差分进化算法。

变异：

差分进化算法中有如下规定：其变异向量通过下面的方式产生。

其中三个x为种群中任取的三个个体，F为变异算子，有时会随着迭代次数而发生改变。变异操作不是在原有种群上的操作，而是利用原有种群，直接生成了一个新的种群，称为变异种群。这一点跟遗传算法极为不同。

交叉：

差分进化算法一定是先变异，再进行交叉，因为交叉是这样规定的：

生成一个随机数j,j和预先定义好的交叉算子CR比大小。如果j大，把变异种群的某一列染色体给交叉种群，否则把原种群的某一列染色体给变异种群。交叉算子CR的取值在0~1之间。

这里参考了《智能优化算法及其matlab实例第二版》的说法，把交叉操作产生的新种群称为交叉种群，但其实我个人理解，就类似遗传算法中产生的新一代种群，最后把新种群和初代种群放在一起用适应度函数进行筛选，思路的本质是不变的。这里进行交叉目的也是为了增加种群的扰动因素。

选择：

这个就跟遗传算法类似了，用适应的函数去评估新的种群与原始种群，从里面挑好的出来组成下一代，这部分就略过。

代码实现

这里选的例子其实是十个变量让其平方和最小，我在这篇博客里面有利用遗传算法对其进行优化求解，以及对问题的详细说明，感兴趣的同学可以对比着看一下：

Python-遗传算法君主交叉代码实现

下面直接上代码了，都是很常规的操作，没有什么特殊的处理，所以就不讲解代码了。

import numpy as np
import random
import matplotlib.pyplot as plt
import math as mt
#import seaborn as sns
#sns.set_style('darkgrid')

def funcl(x):
    y=0
    for i in range(len(x)):
        y=y+x[i]**2
    return y
   
#%%
NP=50   #初始化种群数
D=10    #单条染色体基因数目
CR=0.1  #交叉算子
F0=0.4  #初始变异算子
G=200   #最大遗传代数
Xs=20   #上限
Xx=-20    #下限

jiyi=np.random.rand(NP,D)
f=jiyi*(Xs-Xx)+Xx                              #随机获得初始种群
FIT=[]                #适应度计算存储列表
trace=[]
xtrace=[]
for i in range(NP):
    FIT.append(funcl(f[i]))


#%%差分进化循环
for i in range(G):
    print(i)
    vec=[]               #变异种群,没看懂但是都是2维的
    u=[[]for i in range(NP)]                 #选择种群
    lamda=mt.exp(1-G/(G-i))     #自适应变异算子，随着迭代次数发生变化，之后可以讨论一下
    F=F0*(2**lamda)
    #变异操作，和遗传算法的变异不同！,得到任意两个个体的差值，与变异算子相乘加第三个个体
    for m in range(NP):
        r1=random.sample(range(0,NP),1)[0]
        while r1==m:
            r1=random.sample(range(0,NP),1)[0]
        r2=random.sample(range(0,NP),1)[0]
        while r2==m or r2==r1:
            r2=random.sample(range(0,NP),1)[0]
        r3=random.sample(range(0,NP),1)[0]
        while r3==m or r3==r2 or r3==r1:
            r3=random.sample(range(0,NP),1)[0]
        vec.append(f[r1]+F*(f[r2]-f[r3]))
    
    #交叉操作,交叉所有个体的第j维
    r=random.sample(range(0,NP),1)[0]
    for j in range(D):
        cr=np.random.rand()
        tem=[]
        if cr<=CR or j==r:
            for k in range(len(f)):
                u[k].append(vec[k][j])  #添加所有个体的第j维
        else:
            for k in range(len(f)):
                u[k].append(f[k][j])
            
    #边界条件处理
    for j in range(NP):
        for m in range(D):
            if u[j][m]Xs:
                u[j][m]=np.random.rand()*(Xs-Xx)+Xx #因为vec是变异得到的，所以不一定在取值范围之内
            else:
                continue
    #选择操作
    FIT1=[]
    for m in range(NP):
        FIT1.append(funcl(u[m]))
    for m in range(NP):
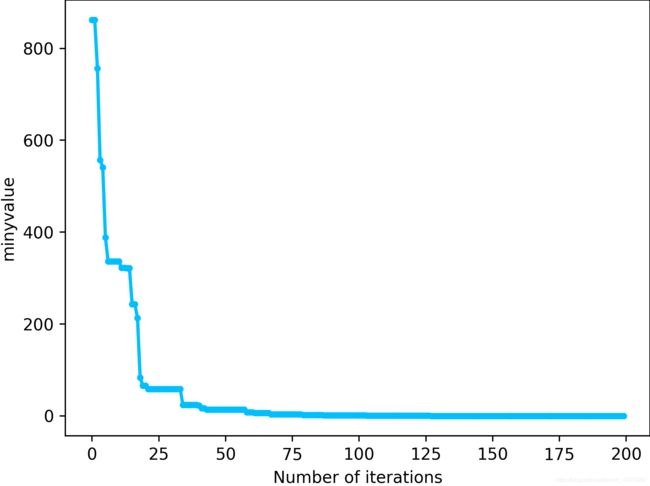
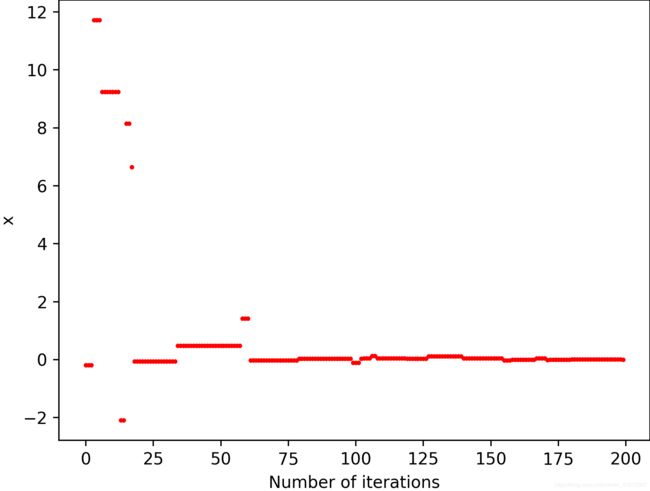
        if FIT1[m]

结果展示

收敛速度还是很快的，下面是对应的y值以及其中一个x的收敛情况。需要提出来强调的是，差分进化算法真的速度特别快，遗传算法求解的时候，需要等待一段时间，但是差分进化基本上是秒出结果，很厉害。

 

 参考资料

[1]差分进化算法-百度百科

[2]《智能优化算法及其matlab实例第二版》