3 基于采样的路径规划 —— RRT算法
文章目录
- RRT—— 快速扩展随机算法
- 算法步骤
-
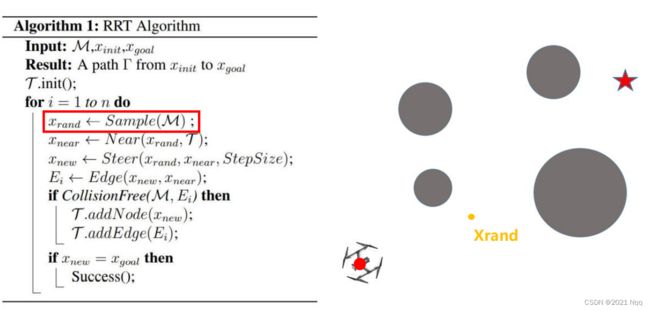
- 1. 生成随机点 Xrand
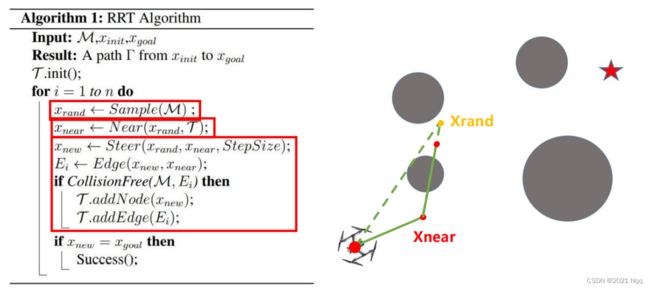
- 2. 寻找距离 Xrand 最近的节点 Xnear
- 3. 生成新的节点 Xnew
- 4. 再次采样 Xrand,寻找距离最近的节点 Xnear
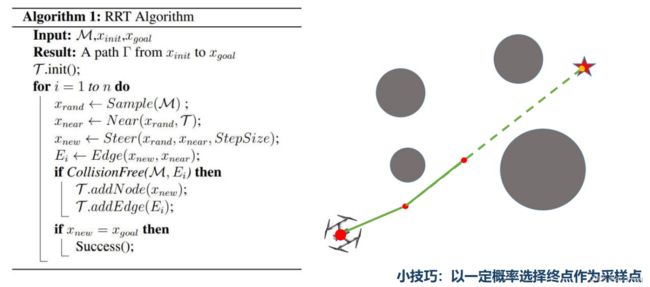
- 5. 继续采样,随着采样的进行越来越靠近终点
- 6. 以一定概率选择终点最为采样点
- class RRT
-
- def `_init_` 初始化
- def rrt_planning
-
- class Node 设置节点
- def sample 获取采样点
- def get_nearest_list_index 找到距离采样点最近的节点下标
- theta 求解最近节点和采样点之间的角度,生成新节点方向
- def get_new_node 得到新的结点
- def check_segment_collision 判断障碍物是否在Xnew和Xnear的线段上
-
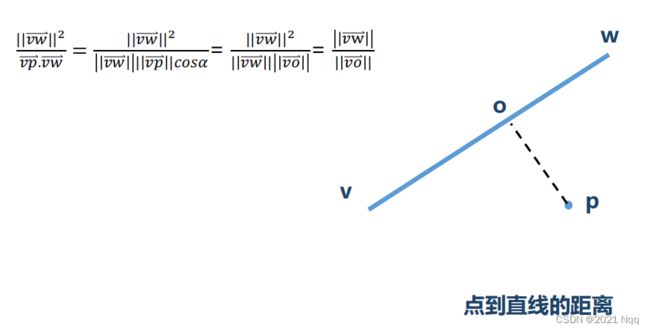
- def distance_squared_point_to_segment 计算点到直线的距离(重难点)
- def is_near_goal 判断是否到了终点附近
-
- def line_cost 计算两点间的距离
- def get_final_course 找路径
- RRT 完整代码
RRT—— 快速扩展随机算法
算法步骤
1. 生成随机点 Xrand
2. 寻找距离 Xrand 最近的节点 Xnear
3. 生成新的节点 Xnew
树的具体生长:将Xnear和Xrand连接起来作为树具体的生长方向,设置步长(stepsize)作为树枝的长度,产生新的节点 Xnew
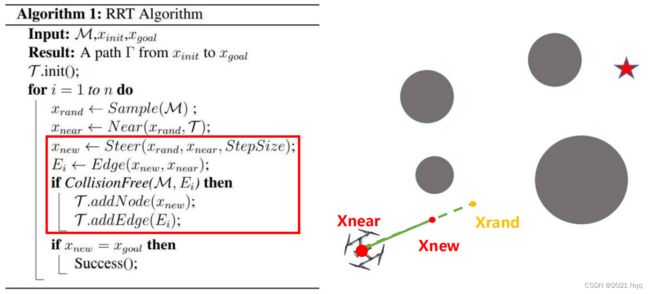
4. 再次采样 Xrand,寻找距离最近的节点 Xnear
5. 继续采样,随着采样的进行越来越靠近终点
设置提前停止的方法:每次生成Xnew节点,都会把该点和终点进行连线,判断之间的距离是否小于步长且没有障碍物,这样就直接把该点和终点连起来。
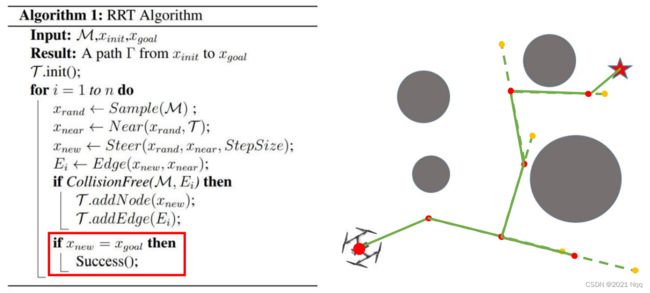
6. 以一定概率选择终点最为采样点
class RRT
def _init_ 初始化
def __init__(self, obstacleList, randArea = [-2,18], expandDis = 2.0, goalSampleRate = 10, maxIter = 200):
self.start = None
self.goal = None
self.min_rand = randArea[0] # 采样范围赋值给最小值和最大值
self.max_rand = randArea[1] # randArea = [-2, 18]
self.expand_dis = expandDis # 设定步长为2
self.goal_sample_rate = goalSampleRate # 目标采样率,有10%的概率每次将终点作为采样点
self.max_iter = maxIter # 设置最大迭代次数为200
self.obstacle_list = obstacleList # 设置障碍物位置和大小
self.node_list = None # 存储RRT树上节点
- 障碍物设置
# 设置障碍物 (x,y,r)最后参数是半径
obstacleList = [ (3, 3, 1.5), (12, 2, 3), (3, 9, 2), (9, 11, 2),]
def rrt_planning
class Node 设置节点
class Node:
def __init__(self, x, y):
self.x = x
self.y = y
self.cost = 0.0
self.parent = None
def sample 获取采样点
- random.randint(start, stop):返回指定范围内的整数
- random.uniform 返回一个随机浮点数 N ,当 a <= b 时 a <= N <= b ,当 b < a 时 b <= N
<= a
def sample(self):
# randint 是在指定的某个区间内的一个值, 产生(0,100)的随机整数, ,[low,high]左闭右闭
if random.randint(0, 100) > self.goal_sample_rate: # goal_sample_rate = 10
# random.uniform 返回一个随机浮点数 N ,当 a <= b 时 a <= N <= b ,当 b < a 时 b <= N <= a
rnd = [random.uniform(self.min_rand, self.max_rand), random.uniform(self.min_rand, self.max_rand)]
# random.uniform(a,b) 返回a、b之间的随机浮点值, [a,b], min_read = -2 max_read = 18
else: # goal point sampling
rnd = [self.goal.x, self.goal.y] # 以终点作为采样点,返回终点坐标,goal = [15, 12]
return rnd
def get_nearest_list_index 找到距离采样点最近的节点下标
def get_nearest_list_index(nodes, rnd):
# 遍历当前所有的节点,计算采样点和每个节点的距离
dList = [(node.x - rnd[0]) ** 2 + (node.y - rnd[1]) ** 2 for node in nodes]
minIndex = dList.index(min(dList)) # 得到列表里距离值最小的下标,dList是列表格式,index最小值的下标
return minIndex # 返回下标
theta 求解最近节点和采样点之间的角度,生成新节点方向
theta = math.atan2(rnd[1] - nearestNode.y, rnd[0] - nearestNode.x)
def get_new_node 得到新的结点
# 生成新的节点, n_ind表示离采样点最近节点的下标,nearestNode表示离采样点最近的节点(用x,y表示)
def get_new_node(self, theta, n_ind, nearestNode):
newNode = copy.deepcopy(nearestNode) # 拷贝最近的节点作为新的节点,然后再增加x,y轴方向的坐标
# 进行生长,生长的距离(设置为2)乘以余弦正弦值,得到节点的坐标,expand_dis = 2
newNode.x += self.expand_dis * math.cos(theta)
newNode.y += self.expand_dis * math.sin(theta)
newNode.cost += self.expand_dis # cost值等于长度,记录长度
newNode.parent = n_ind # 记录这个新节点的父节点,就是 nearestNode 的下标
return newNode
def check_segment_collision 判断障碍物是否在Xnew和Xnear的线段上
def check_segment_collision(self, x1, y1, x2, y2): # 把生成的新节点和最近的节点输入进来
for (ox, oy, size) in self.obstacle_list: # 遍历所有障碍物
# 判断直线和圆是否相切,只需要判断圆心到直线的距离
# 输入 Xnew, Xnear, 障碍物圆心
# array处理向量的模块
dd = self.distance_squared_point_to_segment(
np.array([x1, y1]),
np.array([x2, y2]),
np.array([ox, oy]))
if dd <= size ** 2: # 距离大于半径则没有碰撞
return False # collision
return True
def distance_squared_point_to_segment 计算点到直线的距离(重难点)
- 点到直线的公式(用向量表示)
- 下面公式的值是一个比例,vw与vo的长度比例 = 向量vw的自乘和向量 vp与 vw乘积的比值
python中dot函数用法
- dot()函数可以通过NumPy库调用,也可以由数组实例对象进行调用。例如:a.dot(b) 与 np.dot(a,b)效果相同。但矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的
# 计算点到直线的距离
def distance_squared_point_to_segment(v, w, p):
# Return minimum distance between line segment vw and point p
# 如果端点v,w是同一个点,则距离就是p到v/w的距离,变成点到点的距离
if np.array_equal(v, w):
# a.dot(b) 与 np.dot(a, b) 效果相同
return (p - v).dot(p - v) # v == w case,返回距离的平方(向量(p-v)的x^2+y^2)
l2 = (w - v).dot(w - v) # i.e. |w-v|^2 - avoid a sqrt 计算w和v的线段长度的平方
# Consider the line extending the segment,
# parameterized as v + t (w - v).
# We find projection of point p onto the line.
# It falls where t = [(p-v) . (w-v)] / |w-v|^2
# We clamp t from [0,1] to handle points outside the segment vw.
t = max(0, min(1, (p - v).dot(w - v) / l2)) # (p - v) 与 (w - v)做点积,就是向量pv与向量wv做乘积,t是个比例
projection = v + t * (w - v) # Projection falls on the segment 图中的o点
return (p - projection).dot(p - projection) # 返回p 和 o点的距离的平方
def is_near_goal 判断是否到了终点附近
def is_near_goal(self, node):
d = self.line_cost(node, self.goal) # 计算新加入点和终点的距离
if d < self.expand_dis: # 距离小于步长的话,则表示和终点非常接近,可以直接和终点连起来
return True
return False
def line_cost 计算两点间的距离
def line_cost(node1, node2):
return math.sqrt((node1.x - node2.x) ** 2 + (node1.y - node2.y) ** 2)
def get_final_course 找路径
def get_final_course(self, lastIndex): # 找路径,传入终点值
path = [[self.goal.x, self.goal.y]]
while self.node_list[lastIndex].parent is not None: # 当parent = 0是就找到终点了
node = self.node_list[lastIndex]
path.append([node.x, node.y])
lastIndex = node.parent
path.append([self.start.x, self.start.y])
return path
RRT 完整代码
import copy
import math
import random
import time
import matplotlib.pyplot as plt
from scipy.spatial.transform import Rotation as Rot
import numpy as np
show_animation = True
class RRT:
def __init__(self, obstacleList, randArea = [-2,18], expandDis = 2.0, goalSampleRate = 10, maxIter = 200):
self.start = None
self.goal = None
self.min_rand = randArea[0] # 采样范围赋值给最小值和最大值
self.max_rand = randArea[1] # randArea = [-2, 18]
self.expand_dis = expandDis # 设定步长为2
self.goal_sample_rate = goalSampleRate # 目标采样率,有10%的概率每次将终点作为采样点
self.max_iter = maxIter # 设置最大迭代次数为200
self.obstacle_list = obstacleList # 设置障碍物位置和大小
self.node_list = None # 存储RRT树上节点
# start = [0, 0], goal = [15, 12], animation = show_animation (开头设置show_animation = True)
def rrt_planning(self, start, goal, animation = True):
start_time = time.time() # 进行计时,统计时间
self.start = Node(start[0], start[1]) # 将起点和终点以node节点的方式存储起来,start[0]表示起点x值
self.goal = Node(goal[0], goal[1]) # Node 是一个类 class Node
self.node_list = [self.start] # 将起点加入到node列表中,起点作为根节点
path = None
for i in range(self.max_iter): # 进行for循环,到最大迭代次数200
rnd = self.sample() # 获取采样点rnd
# 求采样点和节点的距离,返回采样点和各个节点距离值最小的节点的下标 n_ind
n_ind = self.get_nearest_list_index(self.node_list, rnd)
nearestNode = self.node_list[n_ind] # 使用下标找到距离采样点最近的节点 Xnear
# steer
theta = math.atan2(rnd[1] - nearestNode.y, rnd[0] - nearestNode.x) # 求解最近节点和采样点之间的角度
newNode = self.get_new_node(theta, n_ind, nearestNode) # 生长过程,生成新的节点
noCollision = self.check_segment_collision(newNode.x, newNode.y, nearestNode.x, nearestNode.y)
if noCollision: # 没有碰撞,就可以把新的节点加入到树里面
self.node_list.append(newNode)
if animation:
self.draw_graph(newNode, path)
# 判断是否到了终点附近
if self.is_near_goal(newNode):
if self.check_segment_collision(newNode.x, newNode.y,
self.goal.x, self.goal.y): # 判断路径是否与障碍物发生碰撞
lastIndex = len(self.node_list) - 1 # 没有碰撞的话就找到终点,下标从0开始,长度减1
path = self.get_final_course(lastIndex)
pathLen = self.get_path_len(path)
print("current path length: {}, It costs {} s".format(pathLen, time.time()-start_time))
if animation:
self.draw_graph(newNode, path)
return path
def rrt_star_planning(self, start, goal, animation=True):
start_time = time.time()
self.start = Node(start[0], start[1])
self.goal = Node(goal[0], goal[1])
self.node_list = [self.start]
path = None
lastPathLength = float('inf')
for i in range(self.max_iter): # 迭代次数
rnd = self.sample() # 获取采样点
# 找离采样点最近的节点,最开始找的离初始点近的结点(有步长)
n_ind = self.get_nearest_list_index(self.node_list, rnd)
nearestNode = self.node_list[n_ind] # 由索引得到距离最近的节点
# steer
theta = math.atan2(rnd[1] - nearestNode.y, rnd[0] - nearestNode.x) # 求解采样点和最近的节点的角度值
newNode = self.get_new_node(theta, n_ind, nearestNode) # 由角度、最近点的父节点的索引值、最近节点得到新的节点
# 判断是否有障碍物
noCollision = self.check_segment_collision(newNode.x, newNode.y, nearestNode.x, nearestNode.y)
if noCollision:
nearInds = self.find_near_nodes(newNode)
newNode = self.choose_parent(newNode, nearInds)
self.node_list.append(newNode)
self.rewire(newNode, nearInds)
if animation:
self.draw_graph(newNode, path)
if self.is_near_goal(newNode):
if self.check_segment_collision(newNode.x, newNode.y,
self.goal.x, self.goal.y):
lastIndex = len(self.node_list) - 1
tempPath = self.get_final_course(lastIndex)
tempPathLen = self.get_path_len(tempPath)
if lastPathLength > tempPathLen:
path = tempPath
lastPathLength = tempPathLen
print("current path length: {}, It costs {} s".format(tempPathLen, time.time()-start_time))
return path
def informed_rrt_star_planning(self, start, goal, animation=True):
start_time = time.time()
self.start = Node(start[0], start[1])
self.goal = Node(goal[0], goal[1])
self.node_list = [self.start]
# max length we expect to find in our 'informed' sample space,
# starts as infinite
cBest = float('inf')
path = None
# Computing the sampling space
cMin = math.sqrt(pow(self.start.x - self.goal.x, 2)
+ pow(self.start.y - self.goal.y, 2))
xCenter = np.array([[(self.start.x + self.goal.x) / 2.0],
[(self.start.y + self.goal.y) / 2.0], [0]])
a1 = np.array([[(self.goal.x - self.start.x) / cMin],
[(self.goal.y - self.start.y) / cMin], [0]])
e_theta = math.atan2(a1[1], a1[0])
# 论文方法求旋转矩阵(2选1)
# first column of identity matrix transposed
# id1_t = np.array([1.0, 0.0, 0.0]).reshape(1, 3)
# M = a1 @ id1_t
# U, S, Vh = np.linalg.svd(M, True, True)
# C = np.dot(np.dot(U, np.diag(
# [1.0, 1.0, np.linalg.det(U) * np.linalg.det(np.transpose(Vh))])),
# Vh)
# 直接用二维平面上的公式(2选1)
C = np.array([[math.cos(e_theta), -math.sin(e_theta), 0],
[math.sin(e_theta), math.cos(e_theta), 0],
[0, 0, 1]])
for i in range(self.max_iter):
# Sample space is defined by cBest
# cMin is the minimum distance between the start point and the goal
# xCenter is the midpoint between the start and the goal
# cBest changes when a new path is found
rnd = self.informed_sample(cBest, cMin, xCenter, C)
n_ind = self.get_nearest_list_index(self.node_list, rnd)
nearestNode = self.node_list[n_ind]
# steer
theta = math.atan2(rnd[1] - nearestNode.y, rnd[0] - nearestNode.x)
newNode = self.get_new_node(theta, n_ind, nearestNode)
noCollision = self.check_segment_collision(newNode.x, newNode.y, nearestNode.x, nearestNode.y)
if noCollision:
nearInds = self.find_near_nodes(newNode)
newNode = self.choose_parent(newNode, nearInds)
self.node_list.append(newNode)
self.rewire(newNode, nearInds)
if self.is_near_goal(newNode):
if self.check_segment_collision(newNode.x, newNode.y,
self.goal.x, self.goal.y):
lastIndex = len(self.node_list) - 1
tempPath = self.get_final_course(lastIndex)
tempPathLen = self.get_path_len(tempPath)
if tempPathLen < cBest:
path = tempPath
cBest = tempPathLen
print("current path length: {}, It costs {} s".format(tempPathLen, time.time()-start_time))
if animation:
self.draw_graph_informed_RRTStar(xCenter=xCenter,
cBest=cBest, cMin=cMin,
e_theta=e_theta, rnd=rnd, path=path)
return path
def sample(self):
# randint 是在指定的某个区间内的一个值, 产生(0,100)的随机整数, ,[low,high]左闭右闭
if random.randint(0, 100) > self.goal_sample_rate: # goal_sample_rate = 10
# random.uniform 返回一个随机浮点数 N ,当 a <= b 时 a <= N <= b ,当 b < a 时 b <= N <= a
rnd = [random.uniform(self.min_rand, self.max_rand), random.uniform(self.min_rand, self.max_rand)]
# random.uniform(a,b) 返回a、b之间的随机浮点值, [a,b], min_read = -2 max_read = 18
else: # goal point sampling
rnd = [self.goal.x, self.goal.y] # 以终点作为采样点,返回终点坐标,goal = [15, 12]
return rnd
def choose_parent(self, newNode, nearInds):
if len(nearInds) == 0:
return newNode
dList = []
for i in nearInds:
dx = newNode.x - self.node_list[i].x
dy = newNode.y - self.node_list[i].y
d = math.hypot(dx, dy)
theta = math.atan2(dy, dx)
if self.check_collision(self.node_list[i], theta, d):
dList.append(self.node_list[i].cost + d)
else:
dList.append(float('inf'))
minCost = min(dList)
minInd = nearInds[dList.index(minCost)]
if minCost == float('inf'):
print("min cost is inf")
return newNode
newNode.cost = minCost
newNode.parent = minInd
return newNode
def find_near_nodes(self, newNode):
n_node = len(self.node_list)
r = 50.0 * math.sqrt((math.log(n_node) / n_node))
d_list = [(node.x - newNode.x) ** 2 + (node.y - newNode.y) ** 2
for node in self.node_list]
near_inds = [d_list.index(i) for i in d_list if i <= r ** 2]
return near_inds
def informed_sample(self, cMax, cMin, xCenter, C):
if cMax < float('inf'):
r = [cMax / 2.0,
math.sqrt(cMax ** 2 - cMin ** 2) / 2.0,
math.sqrt(cMax ** 2 - cMin ** 2) / 2.0]
L = np.diag(r)
xBall = self.sample_unit_ball()
rnd = np.dot(np.dot(C, L), xBall) + xCenter
rnd = [rnd[(0, 0)], rnd[(1, 0)]]
else:
rnd = self.sample()
return rnd
@staticmethod
def sample_unit_ball():
a = random.random()
b = random.random()
if b < a:
a, b = b, a
sample = (b * math.cos(2 * math.pi * a / b),
b * math.sin(2 * math.pi * a / b))
return np.array([[sample[0]], [sample[1]], [0]])
@staticmethod
def get_path_len(path):
pathLen = 0
for i in range(1, len(path)):
node1_x = path[i][0]
node1_y = path[i][1]
node2_x = path[i - 1][0]
node2_y = path[i - 1][1]
pathLen += math.sqrt((node1_x - node2_x)
** 2 + (node1_y - node2_y) ** 2)
return pathLen
@staticmethod
def line_cost(node1, node2):
return math.sqrt((node1.x - node2.x) ** 2 + (node1.y - node2.y) ** 2)
@staticmethod
def get_nearest_list_index(nodes, rnd):
# 遍历当前所有的节点,计算采样点和每个节点的距离
dList = [(node.x - rnd[0]) ** 2 + (node.y - rnd[1]) ** 2 for node in nodes]
minIndex = dList.index(min(dList)) # 得到列表里距离值最小的下标,dList是列表格式,index最小值的下标
return minIndex # 返回下标
# 生成新的节点, n_ind表示离采样点最近节点的下标,nearestNode表示离采样点最近的节点(用x,y表示)
def get_new_node(self, theta, n_ind, nearestNode):
newNode = copy.deepcopy(nearestNode) # 拷贝最近的节点作为新的节点,然后再增加x,y轴方向的坐标
# 进行生长,生长的距离(设置为2)乘以余弦正弦值,得到节点的坐标,expand_dis = 2
newNode.x += self.expand_dis * math.cos(theta)
newNode.y += self.expand_dis * math.sin(theta)
newNode.cost += self.expand_dis # cost值等于长度,记录长度
newNode.parent = n_ind # 记录这个新节点的父节点,就是 nearestNode 的下标
return newNode
def is_near_goal(self, node):
d = self.line_cost(node, self.goal) # 计算新加入点和终点的距离
if d < self.expand_dis: # 距离小于步长的话,则表示和终点非常接近,可以直接和终点连起来
return True
return False
def rewire(self, newNode, nearInds):
n_node = len(self.node_list)
for i in nearInds:
nearNode = self.node_list[i]
d = math.sqrt((nearNode.x - newNode.x) ** 2
+ (nearNode.y - newNode.y) ** 2)
s_cost = newNode.cost + d
if nearNode.cost > s_cost:
theta = math.atan2(newNode.y - nearNode.y,
newNode.x - nearNode.x)
if self.check_collision(nearNode, theta, d):
nearNode.parent = n_node - 1
nearNode.cost = s_cost
@staticmethod
# 计算点到直线的距离
def distance_squared_point_to_segment(v, w, p):
# Return minimum distance between line segment vw and point p
# 如果端点v,w是同一个点,则距离就是p到v/w的距离,变成点到点的距离
if np.array_equal(v, w):
# a.dot(b) 与 np.dot(a, b) 效果相同
return (p - v).dot(p - v) # v == w case,返回距离的平方(向量(p-v)的x^2+y^2)
l2 = (w - v).dot(w - v) # i.e. |w-v|^2 - avoid a sqrt 计算w和v的线段长度的平方
# Consider the line extending the segment,
# parameterized as v + t (w - v).
# We find projection of point p onto the line.
# It falls where t = [(p-v) . (w-v)] / |w-v|^2
# We clamp t from [0,1] to handle points outside the segment vw.
t = max(0, min(1, (p - v).dot(w - v) / l2)) # (p - v) 与 (w - v)做点积,就是向量pv与向量wv做乘积,t是个比例
projection = v + t * (w - v) # Projection falls on the segment 图中的o点
return (p - projection).dot(p - projection) # 返回p 和 o点的距离的平方
def check_segment_collision(self, x1, y1, x2, y2): # 把生成的新节点和最近的节点输入进来
for (ox, oy, size) in self.obstacle_list: # 遍历所有障碍物
# 判断直线和圆是否相切,只需要判断圆心到直线的距离
# 输入 Xnew, Xnear, 障碍物圆心
# array处理向量的模块
# dd 表示两点距离的平方
dd = self.distance_squared_point_to_segment(
np.array([x1, y1]),
np.array([x2, y2]),
np.array([ox, oy]))
if dd <= size ** 2: # 距离的平方大于半径的平方则没有碰撞
return False # collision
return True
def check_collision(self, nearNode, theta, d):
tmpNode = copy.deepcopy(nearNode)
end_x = tmpNode.x + math.cos(theta) * d
end_y = tmpNode.y + math.sin(theta) * d
return self.check_segment_collision(tmpNode.x, tmpNode.y, end_x, end_y)
def get_final_course(self, lastIndex): # 找路径,传入终点值
path = [[self.goal.x, self.goal.y]]
while self.node_list[lastIndex].parent is not None: # 当parent = 0是就找到终点了
node = self.node_list[lastIndex]
path.append([node.x, node.y])
lastIndex = node.parent
path.append([self.start.x, self.start.y])
return path
def draw_graph_informed_RRTStar(self, xCenter=None, cBest=None, cMin=None, e_theta=None, rnd=None, path=None):
plt.clf()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if rnd is not None:
plt.plot(rnd[0], rnd[1], "^k")
if cBest != float('inf'):
self.plot_ellipse(xCenter, cBest, cMin, e_theta)
for node in self.node_list:
if node.parent is not None:
if node.x or node.y is not None:
plt.plot([node.x, self.node_list[node.parent].x], [
node.y, self.node_list[node.parent].y], "-g")
for (ox, oy, size) in self.obstacle_list:
plt.plot(ox, oy, "ok", ms=30 * size)
if path is not None:
plt.plot([x for (x, y) in path], [y for (x, y) in path], '-r')
plt.plot(self.start.x, self.start.y, "xr")
plt.plot(self.goal.x, self.goal.y, "xr")
plt.axis([-2, 18, -2, 15])
plt.grid(True)
plt.pause(0.01)
@staticmethod
def plot_ellipse(xCenter, cBest, cMin, e_theta): # pragma: no cover
a = math.sqrt(cBest ** 2 - cMin ** 2) / 2.0
b = cBest / 2.0
angle = math.pi / 2.0 - e_theta
cx = xCenter[0]
cy = xCenter[1]
t = np.arange(0, 2 * math.pi + 0.1, 0.1)
x = [a * math.cos(it) for it in t]
y = [b * math.sin(it) for it in t]
rot = Rot.from_euler('z', -angle).as_matrix()[0:2, 0:2]
fx = rot @ np.array([x, y])
px = np.array(fx[0, :] + cx).flatten()
py = np.array(fx[1, :] + cy).flatten()
plt.plot(cx, cy, "xc")
plt.plot(px, py, "--c")
def draw_graph(self, rnd=None, path=None):
plt.clf()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if rnd is not None:
plt.plot(rnd.x, rnd.y, "^k")
for node in self.node_list:
if node.parent is not None:
if node.x or node.y is not None:
plt.plot([node.x, self.node_list[node.parent].x], [
node.y, self.node_list[node.parent].y], "-g")
for (ox, oy, size) in self.obstacle_list:
# self.plot_circle(ox, oy, size)
plt.plot(ox, oy, "ok", ms=30 * size)
plt.plot(self.start.x, self.start.y, "xr")
plt.plot(self.goal.x, self.goal.y, "xr")
if path is not None:
plt.plot([x for (x, y) in path], [y for (x, y) in path], '-r')
plt.axis([-2, 18, -2, 15])
plt.grid(True)
plt.pause(0.01)
class Node:
def __init__(self, x, y):
self.x = x
self.y = y
self.cost = 0.0
self.parent = None
def main():
print("Start rrt planning")
# create obstacles
obstacleList = [ # 设置障碍物 (x,y,r)最后参数是半径
(3, 3, 1.5),
(12, 2, 3),
(3, 9, 2),
(9, 11, 2),]
# obstacleList = [(5, 5, 1), (3, 6, 2), (3, 8, 2), (3, 10, 2), (7, 5, 2),
# (9, 5, 2), (8, 10, 1)]
# Set params 类RRT,采样范围[-2,18],障碍物,最大迭代次数
rrt = RRT(randArea = [-2, 18], obstacleList = obstacleList, maxIter = 200)
path = rrt.rrt_planning(start = [0, 0], goal = [15, 12], animation = show_animation) # 传入起点和终点
# path = rrt.rrt_star_planning(start=[0, 0], goal=[15, 12], animation=show_animation)
# path = rrt.informed_rrt_star_planning(start=[0, 0], goal=[15, 12], animation=show_animation)
print("Done!!")
if show_animation and path:
plt.show()
if __name__ == '__main__':
main()