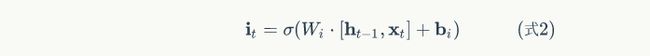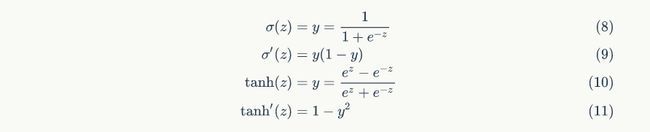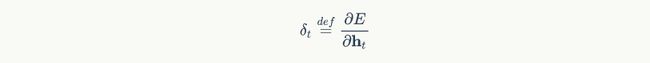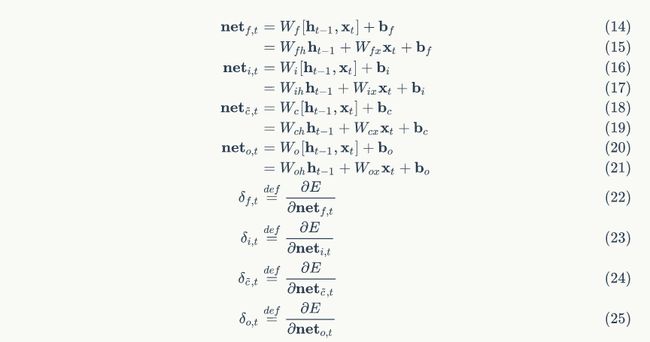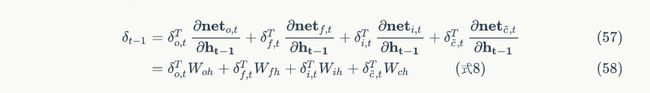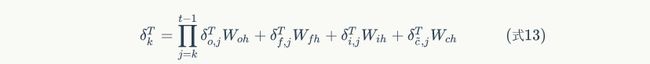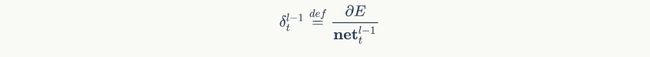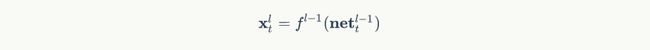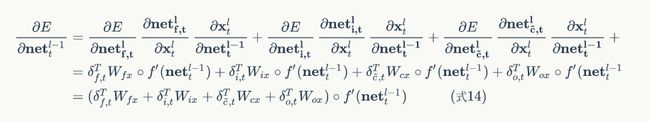【机器学习】长短时记忆网络(LSTM)
文章目录
- 参考文献
- 1. 基本概念
- 2. 长短时记忆网络的前向计算
-
- 2.1 门
- 2.2 遗忘门
- 2.3 输入门
- 2.4 输出门
- 3. 长短时记忆网络的训练
-
- 3.1 LSTM训练算法框架
- 3.2 关于公式和符号的说明
- 3.3 误差项沿时间的反向传递
- 3.4 将误差项传递到上一层
- 3.5 权重梯度的计算
- 4. GRU
-
- 4.1 LSTM与GRU的区别
参考文献
https://github.com/NLP-LOVE/ML-NLP/tree/master/Deep%20Learning/12.2%20LSTM
大部分内容来自https://zybuluo.com/hanbingtao/note/581764,属于个人的学习笔记,侵权必删。
1. 基本概念
长短时记忆网络(Long Short Term Memory Network, LSTM),它成功的解决了原始循环神经网络的缺陷,成为当前最流行的RNN,在语音识别、图片描述、自然语言处理等许多领域中成功应用。
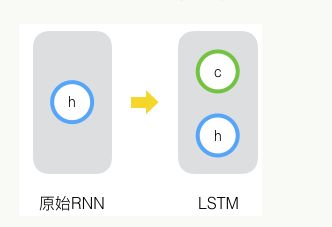
原始RNN无法处理长距离依赖,原始RNN的隐藏层只有一个状态,即h,它对于短期的输入非常敏感。
长短时记忆网络在RNN的基础上再增加一个状态c,让它来保存长期的状态。
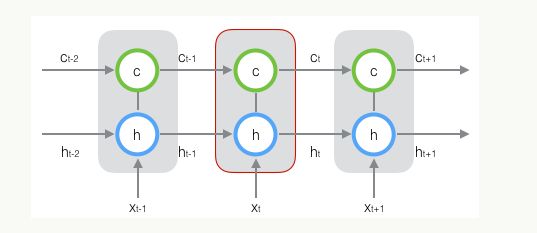
新增加的状态c,称为单元状态(cell state)。我们把上图按照时间维度展开:
我们可以看出,在t时刻,LSTM的输入有三个:当前时刻网络的输入值 x t x_t xt、上一时刻LSTM的输出值 h t − 1 h_{t-1} ht−1、以及上一时刻的单元状态 c t − 1 c_{t-1} ct−1;
LSTM的输出有两个:当前时刻LSTM输出值 h t h_t ht、和当前时刻的单元状态 c t c_t ct。注意 x x x、 h h h、 c c c都是向量,如无特别说明,下文x,h,c不带下标时均表示向量。
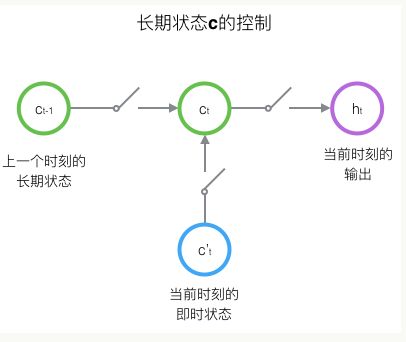
LSTM的关键,就是怎样控制长期状态c。在这里,LSTM的思路是使用三个控制开关。
-
第一个开关,负责控制继续保存长期状态c;
-
第二个开关,负责控制把即时状态输入到长期状态c;
-
第三个开关,负责控制是否把长期状态c作为当前的LSTM的输出。三个开关的作用如下图所示:
接下来,我们要描述一下,输出h和单元状态c的具体计算方法。
2. 长短时记忆网络的前向计算
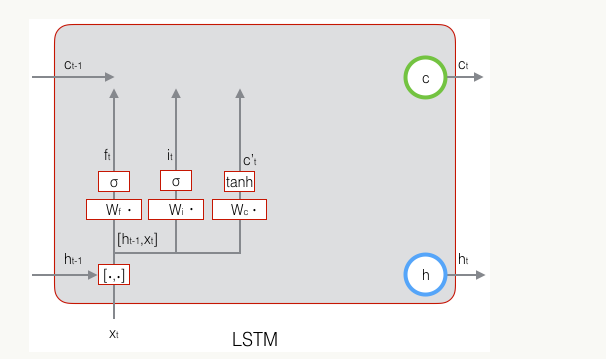
2.1 门
前文描述的开关在算法实现中使用门(gate)。门实际上是一层全连接层,它的输入是一个向量,输出是一个[0,1]的实数向量(一般使用sigmoid函数)。
门的使用,就是用门的输出向量按元素乘以我们需要控制的那个向量。
因为门的输出是0到1之间的实数向量,那么,当门输出为0时,任何向量与之相乘都会得到0向量,这就相当于啥都不能通过;输出为1时,任何向量与之相乘都不会有任何改变,这就相当于啥都可以通过。因为 σ \sigma σ的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c的内容:
- 遗忘门(forget gate),决定上一时刻的单元状态 c t − 1 c_{t-1} ct−1有多少保留到当前时刻 c t c_t ct;
- 输入门(input gate),决定了当前时刻网络的输入 x t x_t xt有多少保存到单元状态 c t c_t ct。
LSTM用输出门(output gate)来控制单元状态 c t c_t ct有多少输出到LSTM的当前输出值 h t h_t ht。
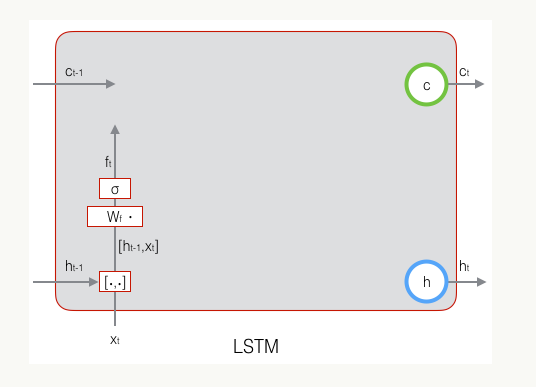
2.2 遗忘门
上式中, W f W_f Wf是遗忘门的权重矩阵, [ h t − 1 , x t ] [h_{t-1},x_t] [ht−1,xt]表示把两个向量连接成一个更长的向量, b f b_f bf是遗忘门的偏置项, σ \sigma σ是sigmoid函数。如果输入的维度是 d x d_x dx,隐藏层的维度是 d h d_h dh,单元状态的维度是 d c d_c dc(通常 d h = d c d_h=d_c dh=dc),则遗忘门的权重矩阵维度是 d c × ( d h + d x ) d_c \times (d_h+d_x) dc×(dh+dx)。
事实上,权重矩阵都是两个矩阵拼接而成的:一个是 W f h W_{fh} Wfh,它对应着输入项 h t − 1 h_{t-1} ht−1,其维度为 d c × d h d_c \times d_h dc×dh;一个是 W f x W_{fx} Wfx,它对应着输入项 x t x_t xt,其维度为 d c × d x d_c \times d_x dc×dx。 W f W_f Wf可以写为:
2.3 输入门
上式中, W i W_{i} Wi是输入门的权重矩阵, b i b_i bi是输入门的偏置项。下图表示了输入门的计算:

接下来,我们计算用于描述当前输入的单元状态 c ~ t \tilde{c}_t c~t,它是根据上一次的输出和本次输入来计算的:
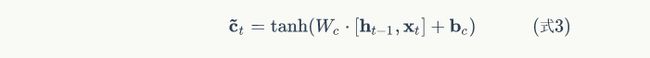
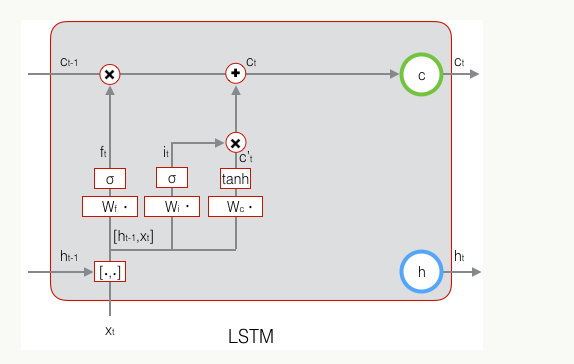
现在,我们计算当前时刻的单元状态 c t c_t ct。它是由上一次的单元状态 c t − 1 c_{t-1} ct−1按元素乘以遗忘门 f t f_t ft,再用当前输入的单元状态 c ~ t \tilde{c}_t c~t按元素乘以输入门 i t i_t it,再将两个积加和产生的:
这样,我们就把LSTM关于当前的记忆 c ~ t \tilde{c}_t c~t和长期的记忆 c t − 1 c_{t-1} ct−1组合在一起,形成了新的单元状态 c t c_t ct。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容进入记忆。
2.4 输出门
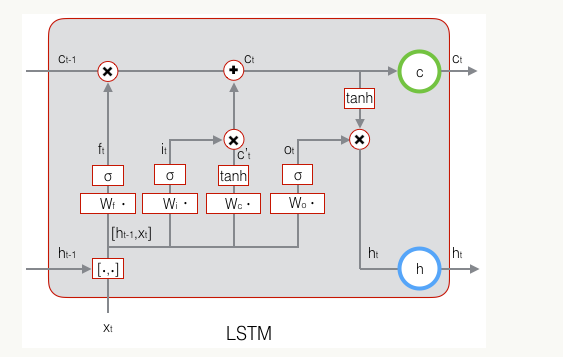
下面,我们要看看输出门,它控制了长期记忆对当前输出的影响:
下图表示LSTM最终输出的计算:
式1到式6就是LSTM前向计算的全部公式。至此,我们就把LSTM前向计算讲完了。
3. 长短时记忆网络的训练
3.1 LSTM训练算法框架
LSTM的训练算法仍然是反向传播算法,对于这个算法,我们已经非常熟悉了。主要有下面三个步骤:
- 前向计算每个神经元的输出值,对于LSTM来说,即 f t f_t ft、 i t i_t it、 c t c_t ct、 o t o_t ot、 h t h_t ht五个向量的值。
- 反向计算每个神经元的误差项值。与循环神经网络一样,LSTM误差项的反向传播也是包括两个方向:一个是沿时间的反向传播,即从当前t时刻开始,计算每个时刻的误差项;一个是将误差项向上一层传播。
- 根据相应的误差项,计算每个权重的梯度。
3.2 关于公式和符号的说明
设定gate的激活函数为sigmoid函数,输出的激活函数为tanh函数。他们的导数分别为:
从上面可以看出,sigmoid和tanh函数的导数都是原函数的函数。这样,我们一旦计算原函数的值,就可以用它来计算出导数的值。
LSTM需要学习的参数共有8组,分别是:遗忘门的权重矩阵和偏置项、输入门的权重矩阵和偏置项、输出门的权重矩阵和偏置项,以及计算单元状态的权重矩阵和偏置项。
因为权重矩阵的两部分在反向传播中使用不同的公式,因此在后续的推导中,权重矩阵 W f W_f Wf、 W i W_i Wi、 W c W_c Wc、 W o W_o Wo都将被写为分开的两个矩阵: W f h W_{fh} Wfh、 W f x W_{fx} Wfx、 W i h W_{ih} Wih、 W i x W_{ix} Wix、 W o h W_{oh} Woh、 W o x W_{ox} Wox、 W c h W_{ch} Wch、 W c x W_{cx} Wcx。
我们解释一下按元素乘o符号。当o作用于两个向量时,运算如下:
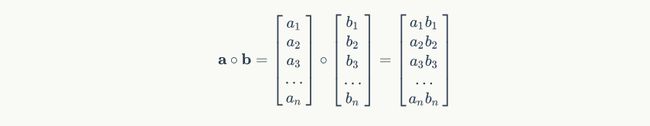
当o作用于一个向量和一个矩阵时,运算如下:
当o作用于两个矩阵时,两个矩阵对应位置的元素相乘。按元素乘可以在某些情况下简化矩阵和向量运算。例如,当一个对角矩阵右乘一个矩阵时,相当于用对角矩阵的对角线组成的向量按元素乘那个矩阵:
![]()
当一个行向量右乘一个对角矩阵时,相当于这个行向量按元素乘那个矩阵对角线组成的向量:
在t时刻,LSTM的输出值为 h t h_t ht。我们定义t时刻的误差项 σ t \sigma_t σt为:
注意,这里假设误差项是损失函数对输出值的导数,而不是对加权输入 n e t t l net_t^l nettl的导数。因为LSTM有四个加权输入,分别对应 f t f_t ft、 i t i_t it、 c t c_t ct、 o t o_t ot,我们希望往上一层传递一个误差项而不是四个。但我们仍然需要定义出这四个加权输入,以及他们对应的误差项。
3.3 误差项沿时间的反向传递
沿时间反向传递误差项,就是要计算出t-1时刻的误差项 σ t − 1 \sigma_{t-1} σt−1
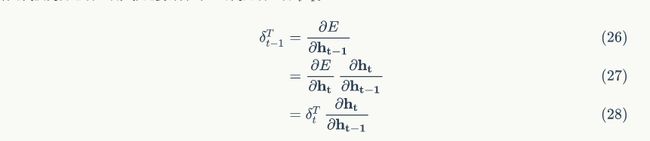
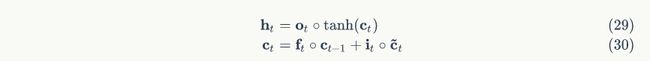
显然, o t o_t ot、 f t f_t ft、 i t i_t it、 c ~ t \tilde{c}_t c~t都是的函数,那么,利用全导数公式可得
:
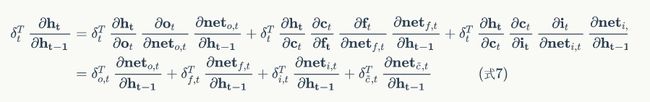
下面,我们要把式7中的每个偏导数都求出来。根据式6,我们可以求出:
式8到式12就是将误差沿时间反向传播一个时刻的公式。有了它,我们可以写出将误差项向前传递到任意k时刻的公式:
3.4 将误差项传递到上一层
我们假设当前为第l层,定义l-1层的误差项是误差函数对l-1层加权输入的导数,即:
本次LSTM的输入 x t x_t xt由下面的公式计算:
上式中, f l − 1 f^{l-1} fl−1表示第l-1层的激活函数。
因为 n e t f , t l net^l_{f,t} netf,tl、 n e t i , t l net^l_{i,t} neti,tl、 n e t c ˉ , t l net^l_{\bar{c},t} netcˉ,tl、 n e t o , t l net^l_{o,t} neto,tl都是 x t x_t xt的函数, x t x_t xt又是 n e t t l − 1 net_t^{l-1} nettl−1的函数,因此,要求出E对 n e t t l − 1 net_t^{l-1} nettl−1的导数,就需要使用全导数公式:
式14就是将误差传递到上一层的公式。
3.5 权重梯度的计算
对于 W f W_f Wf、 W i W_i Wi、 W c W_c Wc、 W o W_o Wo的权重梯度,我们知道它的梯度是各个时刻梯度之和,我们首先求出它们在t时刻的梯度,然后再求出他们最终的梯度。
以上就是LSTM的训练算法的全部公式。
4. GRU
这部分可参考博客。
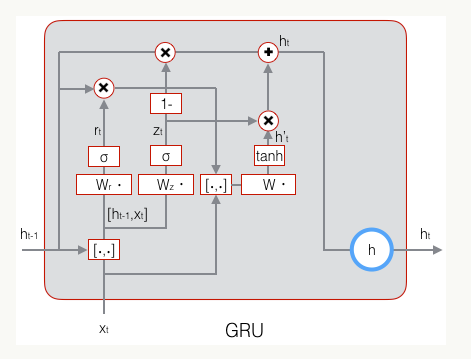
GRU对LSTM做了两个大改动:
- 将输入门、遗忘门、输出门变为两个门:更新门(Update Gate) z t z_t zt和重置门(Reset Gate) r t r_t rt。
- 将单元状态与输出合并为一个状态:h。
4.1 LSTM与GRU的区别
LSTM与GRU二者结构十分相似,不同在于:
- 新的记忆都是根据之前状态及输入进行计算,但是GRU中有一个重置门控制之前状态的进入量,而在LSTM里没有类似门;
- 产生新的状态方式不同,LSTM有两个不同的门,分别是遗忘门(forget gate)和输入门(input gate),而GRU只有一种更新门(update gate);
- LSTM对新产生的状态可以通过输出门(output gate)进行调节,而GRU对输出无任何调节。
- GRU的优点是这是个更加简单的模型,所以更容易创建一个更大的网络,而且它只有两个门,在计算性上也运行得更快,然后它可以扩大模型的规模。
- LSTM更加强大和灵活,因为它有三个门而不是两个。