(七) 三维点云课程---ICP (Point-to-Plane)
三维点云课程—ICP (Point-to-Plane)
由于Point-to-Point的方法不允许平面之间的滑动,故提出了Point-to-Plane的ICP方法
1.Point-to-Plane的原理介绍
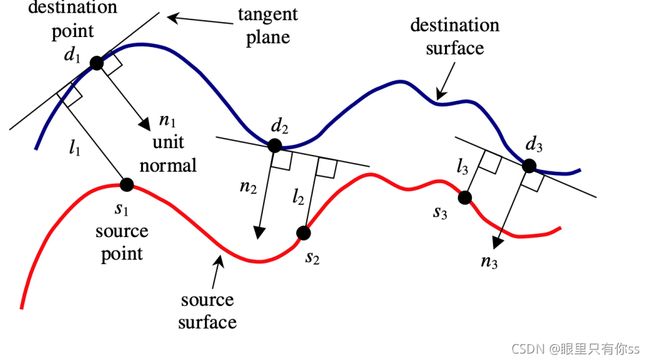
Point-to-Plane不同于Point-to-Point的方法,它是求源点云中的点 p i p_i pi 到目标点云中 q i q_i qi组成的曲面的距离。也就是说,此时点云需要提供每个点的法向量。
数学表述
E ( R , t ) = ∑ i = 1 N ( ( R p i + t − q i ) T n i ) 2 E(R,t)=\sum \limits_{i=1}^N \Big((Rp_i+t-q_i)^Tn_i \Big)^2 E(R,t)=i=1∑N((Rpi+t−qi)Tni)2
其中
源点云(通常是旋转的) P = { p 1 , . . . , p N p } , p i ∈ R 3 P=\{p_1,...,p_{N_p}\},p_i \in R^3 P={p1,...,pNp},pi∈R3
目标点云(参考点云,通常是固定的) Q = { q 1 , . . . , q N 1 } , q i ∈ R 3 Q=\{q_1,...,q_{N_1}\},q_i \in R^3 Q={q1,...,qN1},qi∈R3
每个 q i q_i qi点的法向量 n i n_i ni
对于上式的 E ( R , t ) E(R,t) E(R,t),遗憾的是没有解析解,对于这样的问题,可以采用最小二乘的方法。因为旋转矩阵 R R R有9个元素,但要满足 R R T = I , ∣ R ∣ = 1 RR^T=I,|R|=1 RRT=I,∣R∣=1的约束,故 R R R不能随便选。此时可以采用欧拉角的方式描述旋转矩阵。
定义如下
α \alpha α绕 x x x轴旋转, β \beta β绕 y y y轴旋转, γ \gamma γ绕 z z z轴旋转,那么
R x ( α ) = [ 1 0 0 0 cos α − sin α 0 sin α cos α ] R y ( β ) = [ 1 0 0 0 cos β − sin β 0 sin β cos β ] R z ( γ ) = [ 1 0 0 0 cos γ − sin γ 0 sin γ cos γ ] {R_x}(\alpha ) = \begin{bmatrix} 1&0&0\\ 0&{\cos \alpha }&{ - \sin \alpha }\\ 0&{\sin \alpha }&{\cos \alpha } \end{bmatrix} \\ {R_y}(\beta ) =\begin{bmatrix} 1&0&0\\ 0&{\cos \beta }&{ - \sin \beta }\\ 0&{\sin \beta }&{\cos \beta } \end{bmatrix}\\ {R_z}(\gamma ) = \begin{bmatrix} 1&0&0\\ 0&{\cos \gamma }&{ - \sin \gamma }\\ 0&{\sin \gamma }&{\cos \gamma } \end{bmatrix} Rx(α)=⎣⎡1000cosαsinα0−sinαcosα⎦⎤Ry(β)=⎣⎡1000cosβsinβ0−sinβcosβ⎦⎤Rz(γ)=⎣⎡1000cosγsinγ0−sinγcosγ⎦⎤
因此
R = R z ( γ ) R y ( β ) R x ( α ) = [ 1 0 0 0 cos γ − sin γ 0 sin γ cos γ ] [ 1 0 0 0 cos β − sin β 0 sin β cos β ] [ 1 0 0 0 cos α − sin α 0 sin α cos α ] = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] \begin {aligned} R=R_z(\gamma)R_y(\beta)R_x(\alpha) &=\begin{bmatrix} 1&0&0\\ 0&{\cos \gamma }&{ - \sin \gamma }\\ 0&{\sin \gamma }&{\cos \gamma } \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&{\cos \beta }&{ - \sin \beta }\\ 0&{\sin \beta }&{\cos \beta } \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&{\cos \alpha }&{ - \sin \alpha }\\ 0&{\sin \alpha }&{\cos \alpha } \end{bmatrix}\\ &=\begin{bmatrix} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{bmatrix} \end {aligned} R=Rz(γ)Ry(β)Rx(α)=⎣⎡1000cosγsinγ0−sinγcosγ⎦⎤⎣⎡1000cosβsinβ0−sinβcosβ⎦⎤⎣⎡1000cosαsinα0−sinαcosα⎦⎤=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤
化简得
r 11 = c o s γ c o s β r 12 = − s i n γ c o s α + c o s γ s i n β s i n α r 13 = s i n γ s i n α + c o s γ s i n β c o s α r 21 = s i n γ c o s β r 22 = c o s γ c o s α + s i n γ s i n β s i n α r 23 = − c o s γ s i n α + s i n γ s i n β c o s α r 31 = − s i n β r 32 = c o s β s i n α r 33 = c o s β c o s α \begin {aligned} r_{11}&=cos \gamma cos\beta \\ r_{12}&=-sin \gamma cos \alpha + cos \gamma sin \beta sin \alpha\\ r_{13}&=sin \gamma sin \alpha + cos \gamma sin \beta cos \alpha\\ r_{21}&=sin \gamma cos \beta\\ r_{22}&=cos \gamma cos \alpha + sin \gamma sin \beta sin \alpha\\ r_{23}&=-cos \gamma sin \alpha + sin \gamma sin \beta cos \alpha\\ r_{31}&=-sin \beta\\ r_{32}&=cos \beta sin \alpha \\ r_{33}&=cos \beta cos \alpha \end {aligned} r11r12r13r21r22r23r31r32r33=cosγcosβ=−sinγcosα+cosγsinβsinα=sinγsinα+cosγsinβcosα=sinγcosβ=cosγcosα+sinγsinβsinα=−cosγsinα+sinγsinβcosα=−sinβ=cosβsinα=cosβcosα
这样得到的 R R Rs是一个非线性的矩阵,不能采用最小二乘的方法,需要用高斯牛顿或者列文伯格的犯法,不过特别麻烦。进而采用近似的方法
α , β , γ → 0 c o s θ ≈ 1 , s i n θ ≈ θ , θ 2 ≈ 0 , i f θ ≈ 0 \alpha,\beta,\gamma \to 0\\ cos \theta \approx 1,sin \theta \approx \theta,\theta^2 \approx 0,if \; \; \theta \approx 0 α,β,γ→0cosθ≈1,sinθ≈θ,θ2≈0,ifθ≈0
那么
R ≈ [ 1 α β − γ α γ + β γ α β γ + 1 β γ − α − β α 1 ] ≈ [ 1 − γ β γ 1 − α − β α 1 ] R \approx \begin{bmatrix} 1&{\alpha \beta - \gamma }&{\alpha \gamma + \beta }\\ \gamma &{\alpha \beta \gamma + 1}&{\beta \gamma - \alpha }\\ { - \beta }&\alpha &1 \end{bmatrix} \approx \begin{bmatrix} 1&{ - \gamma }&\beta \\ \gamma &1&{ - \alpha }\\ { - \beta }&\alpha &1 \end{bmatrix} R≈⎣⎡1γ−βαβ−γαβγ+1ααγ+ββγ−α1⎦⎤≈⎣⎡1γ−β−γ1αβ−α1⎦⎤
所以
( R p i + t − q i ) T n i = ( n i z p i y − n i y p i z ) α + ( n i x p i z − n i z p i x ) β + ( n i y p i x − n i x p i y ) γ + n i x t x + n i y t y + n i z t z − ( n i x q i x + n i y q i y + n i z q i z − n i x p i x − n i y p i y − n i z p i z ) (Rp_i+t-q_i)^Tn_i=(n_{iz}p_{iy}-n_{iy}p_{iz})\alpha+(n_{ix}p_{iz}-n_{iz}p_{ix})\beta+(n_{iy}p_{ix}-n_{ix}p_{iy})\gamma\\ +n_{ix}t_x+n_{iy}t_y+n_{iz}t_z\\ -(n_{ix}q_{ix}+n_{iy}q_{iy}+n_{iz}q_{iz}-n_{ix}p_{ix}-n_{iy}p_{iy}-n_{iz}p_{iz}) (Rpi+t−qi)Tni=(nizpiy−niypiz)α+(nixpiz−nizpix)β+(niypix−nixpiy)γ+nixtx+niyty+niztz−(nixqix+niyqiy+nizqiz−nixpix−niypiy−nizpiz)
化成 A x = b Ax=b Ax=b的形式
A = [ a 11 a 12 a 13 n 1 x n 1 y n 1 z a 21 a 22 a 23 n 2 x n 2 y n 2 z . . . . . . . . . . . . . . . . . . a N 1 a N 2 a N 3 n N x n N y n N z ] x = [ α β γ t x t y t z ] b = [ n 1 x q 1 x + n 1 y q 1 y + n 1 z q 1 z − n 1 x p 1 x − n 1 y p 1 y − n 1 z p 1 z n 2 x q 2 x + n 2 y q 2 y + n 2 z q 2 z − n 2 x p 2 x − n 2 y p 2 y − n 2 z p 2 z 0 n N x q N x + n N y q N y + n N z q N z − n N x p N x − n N y p N y − n N z p N z ] \begin {aligned} A&=\begin{bmatrix} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{n_{1x}}}&{{n_{1y}}}&{{n_{1z}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{n_{2x}}}&{{n_{2y}}}&{{n_{2z}}}\\ {...}&{...}&{...}&{...}&{...}&{...}\\ {{a_{N1}}}&{{a_{N2}}}&{{a_{N3}}}&{{n_{Nx}}}&{{n_{Ny}}}&{{n_{Nz}}} \end{bmatrix}\\ x&=\begin{bmatrix} \alpha \\ \beta \\ \gamma \\ {{t_x}}\\ {{t_y}}\\ {{t_z}} \end{bmatrix}\\ b&=\begin{bmatrix} n_{1x}q_{1x}+n_{1y}q_{1y}+n_{1z}q_{1z}-n_{1x}p_{1x}-n_{1y}p_{1y}-n_{1z}p_{1z}\\ n_{2x}q_{2x}+n_{2y}q_{2y}+n_{2z}q_{2z}-n_{2x}p_{2x}-n_{2y}p_{2y}-n_{2z}p_{2z}\\ 0\\ n_{Nx}q_{Nx}+n_{Ny}q_{Ny}+n_{Nz}q_{Nz}-n_{Nx}p_{Nx}-n_{Ny}p_{Ny}-n_{Nz}p_{Nz} \end{bmatrix} \end {aligned} Axb=⎣⎢⎢⎡a11a21...aN1a12a22...aN2a13a23...aN3n1xn2x...nNxn1yn2y...nNyn1zn2z...nNz⎦⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡αβγtxtytz⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎡n1xq1x+n1yq1y+n1zq1z−n1xp1x−n1yp1y−n1zp1zn2xq2x+n2yq2y+n2zq2z−n2xp2x−n2yp2y−n2zp2z0nNxqNx+nNyqNy+nNzqNz−nNxpNx−nNypNy−nNzpNz⎦⎥⎥⎤
其中
a i 1 = n i z p i y − n i y p i z a i 2 = n i x p i z − n i z p i x a i 3 = n i y p i x − n i x p i y a_{i1}=n_{iz}p_{iy}-n_{iy}p_{iz}\\ a_{i2}=n_{ix}p_{iz}-n_{iz}p_{ix}\\ a_{i3}=n_{iy}p_{ix}-n_{ix}p_{iy} ai1=nizpiy−niypizai2=nixpiz−nizpixai3=niypix−nixpiy
最后通过最小二乘的解法 x = ( A T A ) − 1 A T b x=(A^TA)^{-1}A^Tb x=(ATA)−1ATb,解的 x x x在恢复 R , t R,t R,t
2.Point-to-Plane的步骤
给予两组点云集
- 源点云,旋转的 , P = { p 1 , . . . , p N p } , p i ∈ R 3 P=\{p_1,...,p_{N_{p}}\},p_i \in R^3 P={p1,...,pNp},pi∈R3
- 目标点云,固定的, Q = { q 1 , . . . , q N q } , q i ∈ R 3 Q=\{q_1,...,q_{N_{q}}\},q_i\in R^3 Q={q1,...,qNq},qi∈R3
- 数据预处理
- 对每一个点 p i p_i pi在 Q Q Q内寻找最近的邻居
- 移除外点对,如 ∣ ∣ p i − q i ∣ ∣ ||p_i-q_i|| ∣∣pi−qi∣∣太大
- R , t = a r g R , t m i n E ( R , t ) = a r g R , t m i n 1 N ∑ t = 1 N ( ( R p i + t − q i ) T n i ) 2 R,t=arg_{R,t}minE(R,t)=arg_{R,t}min\frac{1}{N}{\sum \limits_{t=1}^N{((Rp_i+t-q_i)^Tn_i)^2}} R,t=argR,tminE(R,t)=argR,tminN1t=1∑N((Rpi+t−qi)Tni)2
- 通过点的三维值和法向量构建 A , x , b A,x,b A,x,b
- x ^ = arg min x E ( x ) = ∣ ∣ A x − b ∣ ∣ 2 = ( A T A ) − 1 A T b \hat x=\arg \mathop {\min }\limits_x E(x)=||Ax-b||^2=(A^TA)^{-1}A^Tb x^=argxminE(x)=∣∣Ax−b∣∣2=(ATA)−1ATb
- x ^ = [ α , β , γ , t x , t y , t z ] T \hat x=[\alpha,\beta,\gamma,t_x,t_y,t_z]^T x^=[α,β,γ,tx,ty,tz]T
- 从 x ^ \hat x x^恢复 R , t R,t R,t
- 校验
- 评估迭代的收敛性
- E ( R , t ) E(R,t) E(R,t)比较小
- Δ R , Δ t \Delta R,\Delta t ΔR,Δt比较小
- 迭代没有终止
- P ← R P + t P \leftarrow RP+t P←RP+t
- 重复1-3步,直至迭代成功。
- 评估迭代的收敛性