机器学习基础简述（一）：决策树

决策树

学习的时候手抄了很多大佬们的笔记，这是从手抄本上重新整理的，有空搜一搜把参考过的大佬们的链接贴上来。

1. 几种常见算法的简单对比

算法类别	算法特点	对比	损失函数
随机森林（RF）	bagging方法，基于样本	对样本进行有放回采样，多次采样来训练不同树，最后投票得到结果
adaboost	boosting方法，基于样本	提高被错分样本的权重，最后加权计分来得到结果，使用的决策树通常为单层决策树（一个决策点）	指数损失函数
梯度下降树(GBDT)	boosting方法，基于残差（前向分布算法）和cart树，决策树加法	引入了残差机制，只用cart树，一阶导数	（1）分类问题可以选用指数损失函数、对数损失函数；（2）回归问题可以选用均方差损失函数、绝对损失函数；（3）huber损失函数和分位数损失函数，也是用于回归问题，可以增加回归问题的健壮性，可以减少异常点对损失函数的影响
XGboost	boosting方法，基于残差，引入了正则化项，二阶导数 ，可用回归树或者分类树	引入了二阶导数和正则项，特征可并行（样本数据预先排序），引入了特征子采样，	损失函数与GBDT同
LightGBM	boosting方法，相比XGboost带来了速率上的优化，性能上其实没什么改动	基于直方图的一系列优化，带深度限制的leaf-wise叶子生长策略，直接支持类别特征，cache命中率优化	与GBDT同

2. 随机森林（RF）

2.1. 模型简介及算法过程

（1）模型

总输入：样本N个（每个样本特征D类）
输入（每轮）：随机抽取的n个样本（有放回），在样本中随机抽取的d类特征
输出（每轮）：所生成的决策树的决策结果
特点：不剪枝，完全并行，树与树之间完全独立毫无依赖

（2）算法过程

1. 首先通过有放回采样（bootstrap）获得n组数据，随机选取特征子集（子特征的数量d通常数量为总特征数的平方根或者对数）
2. 基于每组数据和随机选择的特征子集，构建决策树
3. 集成所有生成的决策树进行决策（因此这些树都尽可能地生长，不会剪枝），这些决策树完全平等（因此不分配权重）

2.2. 损失函数

分类：对数损失函数：
$$L(Y,P(Y\mid X))=-\log P(Y\mid X)=-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^M{y}_{ij}\log \left(p_{ij}\right)$$
对数损失函数的理解：
对数损失是用于最大似然估计的。一组参数在一堆数据下的似然值，等于每一条数据在这组参数下的条件概率之积。而损失函数一般是每条数据的损失之和，为了把积变为和，就取了对数。再加个负号是为了让最大似然值和最小损失对应起来。
回归：均方误差

2.3. 正则化

2.4. 优点和缺点

优点：可并行化，效果好，泛化能力强
缺点：取值划分较多的特征容易产生较大影响，它的原理是减小方差，具有很好的泛化能力，但对应的准确度可能没有减小偏差的方法高。

2. Adaboost

2.1 模型简介及算法过程

（1）输入及输出：
输入：N个样本，每个样本有D个特征，样本权重
总输出：数个单层决策树的决策结果，决策树权重

（2）算法过程

1. 创建一棵单层决策树，得到决策树的决策面，根据该树的误差率，获得决策树权重；
2. 综合所有已有树进行加权表决得到误差率，若该概率大于某个选定阈值，则停止训练，得到最终模型；
3. 增大被错误分类的样本权重，并重复1，2，3过程

（3）数学公式

1. 单棵树的误差率计算：G代表某个基分类器，w代表该分类器中样本的权重
   $$e_m=P\left(G_m\left(x_i\right)\ne y_i\right)=\frac{{\sum }_{i=1}^N{w}_{mi}I\left(G_m\left(x_i\right)\ne y_i\right)}{{\sum }_{i=1}^N{w}_{mi}}=\sum _{i=1}^N{w}_{mi}I\left(G_m\left(x_i\right)\ne y_i\right)$$
   $$\sum _{i=1}^N{w}_{mi}=1$$
2. 单棵树的权重计算：（正确率/错误率）
   $${\alpha }_m=\frac{1}{2}\log \frac{1-e_m}{e_m}$$
3. 样本权重更新：
   $$\begin{array}{l}{W}_{m+1,i}=\frac{w_{mi}\exp \left(-{\alpha }_m{y}_i{G}_m\left(x_i\right)\right)}{{\sum }_{i=1}^N{w}_{mi}\exp \left(-{\alpha }_m{y}_i{G}_m\left(x_i\right)\right)}\end{array}$$
4. 最终分类结果计算：
   $$G(x)=\mathrm{sign}\left(\sum _{m=1}^M{\alpha }_m{G}_m(x)\right)$$

2.2 损失函数

只有指数损失函数：
$$L(y,f(x))=\exp (-yf(x))$$
最小化损失函数：
$$\left({\alpha }_m,G_m(x)\right)=\arg \underset{\alpha ,G}{\min }\sum _{i=1}^N\exp \left(-y_i\left(f_{m-1}\left(x_i\right)+\alpha G\left(x_i\right)\right)\right)$$

2.3 正则化

2.4 优点和缺点

优点：
1、很好的利用了弱分类器进行级联。
2、可以将不同的分类算法作为弱分类器。
3、AdaBoost具有很高的精度。
4、相对于bagging算法和Random Forest算法，AdaBoost充分考虑的每个分类器的权重。
缺点：
1、 弱分类器数目不太好设定，可以使用交叉验证来进行确定。
2、 数据不平衡会明显导致精度下降。
3、 每次都要选最大特征，训练耗时。

3. GBDT

3.1. 模型简介及算法过程

（1）输入及输出
输入：样本
输出：回归树

（2）算法过程

1. 初始化
2. 对样本集中的每个样本，计算损失函数的负梯度在当前模型的值->作为梯度下降的残差。
   对于平方损失函数为，它就是通常所说的残差；而对于一般损失函数，它就是残差的近似值（伪残差）。
   $$r_{mi}=-{\left[\frac{\partial L\left(y_i,f\left(x_i\right)\right)}{\partial f\left(\left(x_i\right)\right)}\right]}_{f(x)=f_{m-1}(x)}$$
3. 我们将残差作为样本对应的y值，拟合一个回归树（因此必须使用cart回归树），得到第m棵树的叶节点区域。对每个叶节点区域，利用线性搜索，估计叶节点区域的值，使损失函数最小化，得到一棵新的回归树。
4. 重复2，3步得到k个回归树。
5. 最终的预测结果是前面这k个回归树结果的加和。

3.2 损失函数

分类树：平方损失，绝对损失，huber损失，分位数损失（后2者的作用是减少异常点对损失函数的影响）。
huber损失：是平方损失和绝对损失的中间产物，对于远离中心的异常点采用绝对损失，而中心附近的点采用平方损失。
$$L(y,f(x))=\{\begin{array}{ll}\frac{1}{2}(y-f(x){)}^2& \text{ if }|y-f(x)|\le \delta \\ \delta \left(|y-f(x)|-\frac{\delta }{2}\right)& \text{ if }|y-f(x)|>\delta \end{array}$$
分位数损失：对应的是分位数回归的损失函数。
$$L(y,f(x))=\sum _{y\ge f(x)}\theta |y-f(x)|+\sum _{y<f(x)}(1-\theta )|y-f(x)|$$

回归树：指数损失函数，对数损失函数。

3.3 正则化

GBDT正则化有三种办法：

1. Shrinkage （衰减算法），即在每一轮迭代获取最终学习器的时候按照一定的步长进行更新。意味着需要更多的迭代次数，通常用步长和迭代最大次数一起来决定算法的拟合效果。
2. subsample（子采样），取值为(0,1]，采用的不放回采样，如果取值为1，则全部样本都使用，等于没有使用子采样；如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合，选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低，推荐在[0.5, 0.8]之间。
3. CART回归树自带的正则化剪枝。

3.4 优点和缺点

主要优点：
可以灵活处理各种类型的数据，包括连续值和离散值。
在相对少的调参时间情况下，预测的准确率也可以比较高。这个是相对SVM来说的。
使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

主要缺点：
由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

（RF不需要进行数据预处理，即特征归一化。而GBDT则需要进行特征归一化。）

4. Xgboost

是BGDT的一种实现，因此基本过程是差不多的，主要从3个方面做了一些优化：
（1）使用了二阶泰勒展开，二阶导数有利于梯度下降的更快更准
（2）添加了模型的复杂程度作为正则项
（3）传统的GBDT采用CART作为基分类器，XGBoost支持多种类型的基分类器，比如线性分类器。
（4）传统的GBDT在每轮迭代时使用全部的数据，XGBoost则采用了与随机森林相似的策略，支持对数据进行采样。
（5）传统的GBDT没有设计对缺失值进行处理，XGBoost能够自动学习出缺失值的处理策略（特征采样）。

4.1 算法过程

1. 迭代生成树T：
2. 迭代初始，对每个样本计算一阶导gi和二阶导hi，该计算只依赖于训练好的树
3. 使用贪心法求解树
4. 新增树后，模型表示为原有的y(t-1)+ft(x)，也就是加上新的树的结果，实践时ft(x)通常要乘以一个参数（叫做步长或者收缩率），其目的是不期望模型每次迭代学习到所有的残差，防止过拟合。

贪心法求解过程：
通常情况下，我们无法枚举所有可能的树结构然后选取最优的，所以我们选择用一种贪婪算法来代替：我们从单个叶节点开始，迭代分裂来给树添加节点，也就是枚举所有特征的所有可能划分，寻找最优分割点。使用一个估计地损失函数来评估切分后的损失函数：

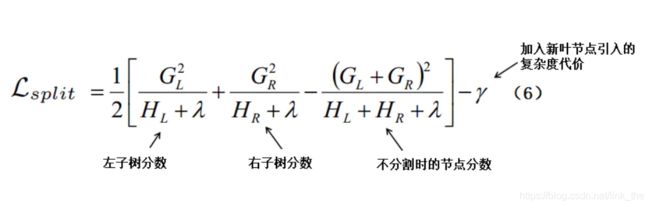
我们的目标是寻找一个特征及对应的值，使得切分后的损失减小程度最大。γ除了控制树的复杂度，另一个作用是作为阈值，只有当分裂后的增益大于γ时，才选择分裂，起到了预剪枝的作用。
该算法要求为连续特征枚举所有可能的切分，这个对计算机要求很高，为了有效做到这一点，XGBoost首先对特征进行排序，然后顺序访问数据，累计loss reduction中的梯度统计量。

4.2 相关公式

每轮迭代时新增树的目标函数：
$${\mathcal{L}}^{(t)}\simeq \sum _{i=1}^n\left[l\left(y_i,{\hat{y}}^{(t-1)}\right)+g_i{f}_t\left({\mathbf{x}}_i\right)+\frac{1}{2}{h}_i{f}_t^2\left({\mathbf{x}}_i\right)\right]+\Omega \left(f_t\right)$$
其中：
$$g_i={\partial }_{{\hat{y}}^{(t-1)}}l\left(y_i,{\hat{y}}^{(t-1)}\right)\text{ and }{h}_i={\partial }_{\hat{y}}^2(t-1)l\left(y_i,{\hat{y}}^{(t-1)}\right)$$
最终目标函数：
${\tilde{\mathcal{L}}}^{(t)}(q)=-\frac{1}{2}{\sum }_{j=1}^T\frac{{\left({\sum }_{i\in I_j}{g}_i\right)}^2}{{\sum }_{i\in I_j}{h}_i+\lambda }+\gamma T$

4.2 损失函数

与GBDT同

4.3 正则化

一次性采用了3种：

1. 正则化项
2. 缩减：通过在每一步的boosting中引入缩减系数，降低每个树和叶子对结果的影响
3. 列采样

4.4 优点和缺点

与GBDT对比：
1.GBDT的基分类器只支持CART树，而XGBoost支持线性分类器，此时相当于带有L1和L2正则项的逻辑回归（分类问题）和线性回归（回归问题）。
2.GBDT在优化时只使用了一阶倒数，而XGBoost对目标函数进行二阶泰勒展开，此外，XGBoost支持自定义损失函数，只要损失函数二阶可导
3.XGBoost借鉴随机森林算法，支持列抽样和行抽样，这样即能降低过拟合风险，又能降低计算。
4.XGBoost在目标函数中引入了正则项，正则项包括叶节点的个数及叶节点的输出值的L2范数。通过约束树结构，降低模型方差，防止过拟合。
5.XGBoost对缺失值不敏感，能自动学习其分裂方向
6.XGBoost在每一步中引入缩减因子，降低单颗树对结果的影响，让后续模型有更大的优化空间，进一步防止过拟合。
7.XGBoost在训练之前，对数据预先进行排序并保存为block，后续迭代中重复使用，减少计算，同时在计算分割点时，可以并行计算
8.可并行的近似直方图算法，树结点在进行分裂时，需要计算每个节点的增益，若数据量较大，对所有节点的特征进行排序，遍历的得到最优分割点，这种贪心法异常耗时，这时引进近似直方图算法，用于生成高效的分割点，即用分裂后的某种值减去分裂前的某种值，获得增益，为了限制树的增长，引入阈值，当增益大于阈值时，进行分裂；

5. LightGBM

改进：
改进了XGboost中的预排序精确贪心算法，这种方法对cache优化不好。支持并行化学习，可处理大规模数据，支持直接使用类别特征。
与SGboost对比：
1.XGBoost采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低，但是不能找到最精确的数据分割点。同时，不精确的分割点可以认为是降低过拟合的一种手段。
2.LightGBM借鉴Adaboost的思想，对样本基于梯度采样，然后计算增益，降低了计算
3.LightGBM对列进行合并，降低了计算
4.XGBoost采样level-wise策略进行决策树的生成，同时分裂同一层的节点，采用多线程优化，不容易过拟合，但有些节点分裂增益非常小，没必要进行分割，这就带来了一些不必要的计算；LightGBM采样leaf-wise策略进行树的生成，每次都选择在当前叶子节点中增益最大的节点进行分裂，如此迭代，但是这样容易产生深度很深的树，产生过拟合，所以增加了最大深度的限制，来保证高效的同时防止过拟合。

6. 通用决策树

6.1 决策树的构造过程

决策树的构造是一个递归过程，其中的每个非叶子节点都表示为一个属性测试，每个分支代表这个特征属性在某个值域上的输出，每个叶子节点存放一个类别，这些样本集合都通过属性测试被划分到子节点中，根节点包含样本全集。
决策树的生成主要分以下两步：（1）节点的分裂：一般当一个节点所代表的属性无法给出判断时，则选择将这一节点分成2个子节点（2）阈值的确定：选择适当的阈值使得分类错误率最小 。
节点分裂终止条件：

1. 当前节点包含的样本都是同一类别，此时该节点标为叶子节点，并设置该节点为对应类别。
2. 属性用完时，无法再继续下分，此时该节点也标为叶子节点，该节点的类别设置为该节点所包含样本最多的类别。
3. 数据用完时，类别设置为父节点中所含样本最多的类别。

6.2 属性划分方法

3个公式：信息熵（信息增益），信息增益率，基尼系数

1. ID3-信息熵（ID3）：对于一组数据，熵越小说明分类结果越好。假定当前样本集合D中第k类样本所占的比例为pk，则样本集合D的信息熵定义为：
   $\mathrm{H}(\mathrm{D})=-{\sum }_{\mathrm{K}=1}^{|\mathrm{K}|}\frac{|{\mathrm{D}}_{\mathrm{k}}|}{|\mathrm{D}|}{\log }_2\frac{|{\mathrm{D}}_{\mathrm{k}}|}{|\mathrm{D}|}$
   信息增益：是决策树中ID3算法中用来进行特征选择的方法，就是用整体的信息熵减掉以按某一特征分裂后的条件熵，结果越大，说明这个特征越能消除不确定性。
   条件熵公式为（假设划分后产生了i个分支子节点）：
   $H(D\mid A)={\sum }_{i=1}^N\frac{|D_i|}{|D|}H\left(D_i\right)$
   信息增益公式为：
   $\mathrm{G}\mathrm{ain}(\mathrm{D},\mathrm{A})=\mathrm{H}(\mathrm{D})-\mathrm{H}(\mathrm{D}\mid \mathrm{A})$

2. 信息增益率（C4.5） ：
   由于信息增益会偏向取值数多的属性，如果遇上有唯一标识的属性那最后会将不确定性减到0，因此引入了信息增益率来控制这个现象，首先用ID3得到信息增益高于平均水平的候选属性，再计算增益率：
   Gainratio $(\mathrm{D},\mathrm{A})=\frac{\mathrm{H}(\mathrm{D})-\mathrm{H}(\mathrm{D}\mid \mathrm{A})}{\mathrm{S}}$
   其中：
   $\mathrm{S}=-{\sum }_{i=1}^k\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$

3. 基尼指数（cart树）：
   基尼指数反映的时从样本集D中随机抽取2个样本，其类别标记不一致的概率，表现的是集合的纯度（类别不一致概率越低，纯度越高，这个子节点的拆分效果越好）。
   $\mathrm{Gini}(D)=1-{\sum }_{k=1}^K{\left(\frac{C_k}{D}\right)}^2$
   当按特征A分裂时，基尼系数的计算如下：
   $\mathrm{Gini}(\mathrm{D},\mathrm{A})={\sum }_{i=1}^N\frac{|D_i|}{|D|}\mathrm{Gini}(Di)$

   为什么要用基尼系数 基尼系数与信息熵计算出来的结果差距很小，但是由于其不用计算对数，因此计算极快。

6.3 剪枝

剪枝的目的：为了对付过拟合
方法：

1. 预剪枝：构造的时候先评估，再考虑是否分支
2. 后剪枝：在构造好后，从下往上评估分支的必要性

6.4 连续值与缺失值处理

1. 连续值离散化：
   常用方法为二分法
2. 缺失值处理：（选择划分属性，分配样本类别）
   （1）如何在属性缺失的情况下选择划分属性？
   选择属性集上没有缺失值的样本子集，计算子集上的信息增益，在城上子集占样本集的比重
   （2）给定划分属性，若某样本在该属性上缺失值，如何划分到具体分支上？
   若样本子集在属性k上缺失，则将该样本以不同的权重（每个分支所含样本比例），将样本划分到所有分支节点中。

6.5 优点和缺点

优点：非参数型，容易解释，能很好地处理缺失特征，对特征空间具有鲁棒性。
缺点：不能在线学习，容易过拟合（因此要剪枝），容易陷入局部最小。