【数据挖掘】第8章 聚类分析: 基本概念和算法

8 聚类分析: 基本概念和算法

---

一、聚类分析概述

1）什么是聚类分析

聚类分析仅根据在数据中发现的描述对象及其关系的信息，将数据对象分组。其目标是， 组内的对象之间是相似的（相关的），而不同的组中的对象是不同的（不相关的）。
组内的相似性（同质性）越大，组间差别越大，聚类就越好。

聚类分析的应用

2）不同的簇类型

簇（Cluster）的定义是不精确的

不同的簇类型

• Well-separated clusters（明显分离的簇）
• Center-based clusters（基于中心的簇）
• Contiguous clusters（基于邻近的簇）
• Density-based clusters （基于密度的簇）
• Property or Conceptual （概念簇）
  

3）聚类算法的分类

大体上，主要的聚类算法可以划分为如下几类：划分方法、层次方法、基于密度的方法、基于网格的方法

1–划分方法
▪ 给定一个有N个元组或者记录的数据集，划分方法将构造K个分组，每一个分组就代表一个聚类，K 1）每一个分组至少包含一个数据记录；
2）每一个数据记录隶属于且仅属于一个分组；
▪ 对于给定的K，算法首先给出一个初始的分组方法，以后通过反复迭代的方法改变分组，使得每一次改进之后分组方案都较前一次好，所谓的“好”的标准就是同一分组的记录越相似越好，而不同分组中的记录则越相异越好。
▪ 最著名与最常用的划分方法是 k-均值方法 和 k-中心点方法。

2–基于层次的方法
▪ 一个层次的聚类方法是将数据对象组成一棵聚类的树。根据层次分解是自底向上还是自顶向下形成，层次的聚类方法可以进一步分为聚合式层次聚类（agglomerative）和分裂式层次聚类（divisive）。
▪ 聚合式的层次聚类，其层次过程的方向是自底向上的。将样本集合中的每个对象作为一个初始簇，然后将最近的两个簇合并，组成新的簇，再将这个新簇与剩余的簇中最近的合并，这种合并过程需要反复进行，直到所有的对象最终被聚到一个簇中。
▪ 分裂式的层次聚类，其层次过程的方向是自顶向下的，最初先将有关对象放到一个簇中，然后将这个簇分裂，分裂的原则是使两个子簇之间的聚类尽可能的远，分裂的过程也反复进行，直到某个终止条件被满足时结束。不论是合并还是分解的过程，都会产生树状结构，树的叶子节点对应各个独立的对象，顶点对应一个包含了所有对象的簇。
▪ 常见的层次聚类算法有：BIRCH算法、CURE算法、ROCK算法等。

3–基于密度的方法
▪ 基于密度的方法与其他方法的一个最根本的区别是：它不是基于各种各样的距离，而是基于密度的，它将簇看做是数据空间中被低密度区域分割开的高密度对象区域，这种方法的优势是善于发现空间数据库中任意形状的聚类。
▪ 基于密度的聚类根据空间密度的差别，把具有相似密度的点作为聚类。由于密度是一个局部概念，这类算法又称为局部聚类（Local Clustering）。一般情况下，基于密度的聚类只扫描一次数据库，故又称为是单次扫描聚类（Single Scan Clustering）。
▪ 基于密度的聚类方法主要：DBSCAN算法、DENCLUE算法。

4–基于网格的方法
▪ 基于网格的方法采用一个多分辨率的网格数据结构。它将数据空间量化，并将其划分为有限数目的网格单元，所有的聚类操作都在网格上进行。该算法的优势在于处理速度快，处理时间与数据对象的数目无关。
▪ 基于网格的聚类方法有STING算法和CLIQUE算法等。

二、K-均值聚类算法

K-means Clustering
K均值是基于原型的、划分的聚类技术。
典型的基于原型的、划分的聚类算法： K均值、 K中心点。

• K均值用 质心 定义原型，其中质心是一组点的均值。 K均值聚类用于n维连续空间中的对象。它试图发现用户指定个数（K）的簇（由质心代表）。
• K中心点使用 中心点 定义原型，其中中心点是一组点中最有代表性的点。K中心点聚类可以用于广泛的数据，因为它只需要对象之间的邻近性度量。尽管质心几乎从来不对应实际的数据点，但是根据定义，中心点必须是一个实际的数据点。

1）基本K均值算法

K均值的算法步骤：首先选择K个初始质心，其中K是用户指定的参数，即所期望的簇的个数。每个点指派到最近的质心，而指派到一个质心的点集为一个簇。然后，根据指派到簇的点，更新每个簇的质心。重复指派和更新步骤，直到簇不发生变化，或等价的，直到质心不发生变化。

算法流程如下：

K-means Clustering: Example

K-均值聚类的距离度量与目标函数
考虑邻近度量为欧几里得距离的数据
度量聚类质量最常用的是误差的平方和(SSE)
▪ 对于每个点, 其误差是到最近质心的距离
▪ 为了得到 SSE, 我们对每个点的误差求平方和   $SSE=\sum _{i=1}^K\sum _{x\in C_i}dis{t}^2(c_i,x)$
▪ $x$是簇 $C_i $的点, $c_i$ 是簇$C_i$的代表点
  可以证明 $c_i$ 对应于簇的质心(均值)   $c_i=\frac{1}{m_i}\sum _{x\in C_i}x$

▪ 给定两个聚类, 我们可以选择具有最小SSE的聚类

其它距离度量
K-means也可以用于非欧氏空间数据
例, 文档数据

• 通常, 文档用余弦相似性度量
  距离是相异性度量, 而余弦是相似性度量
  质心仍然用均值
  最近的质心是最相似的质心
• 目标: 最大化簇中文档与簇的质心的相似性
  总凝聚度   $Totalcohesion=\sum _{i=1}^K\sum _{x\in C_i}cosine(x,c_i)$

K均值：邻近度、质心和目标函数的常见选择

基本K均值算法存在的问题

• 不同的初始质心将收敛得到不同的目标函数，可能只能达到局部最优解。
• 随机选取初始质心，拙劣的初始质心，可能导致很糟糕的聚类结果。
• 可能产生空簇
• 容易受到离群点的影响
• 不能处理非球形簇、不同尺寸和不同密度的簇

1–初始质心问题

解决初始质心的选择问题：
方法1：多次运行，选取最小的SSE
方法2：采用小部分数据，并进行层次聚类得到初始质心
方法3：选择多于K个的初始质心，并在其中选出K个分布广泛的作为初始质心。

• 随机地选择第一个点，或取所有点的质心作为第一个点。然后，对于每个后继初始质心，选择离已经选取过的初始质心最远的点。
• 使用这种方法，确保了选择的初始质心不仅是随机的，而且是散开的。
• 但是，这种方法可能选中离群点。
• 此外，求离当前初始质心集最远的点开销也非常大。为了克服这个问题，通常该方法用于点样本。

2–可能产生空簇
如果所有的点在指派步骤都未分配到某个簇，就会得到空簇。
如果这种情况发生，则需要某种策略来选择一个替补质心，否则的话，平方误差将会偏大。
一种方法是选择一个距离当前任何质心最远的点。这将消除当前对总平方误差影响最大的点。
另一种方法是从具有最大SSE的簇中选择一个替补的质心。这将分裂簇并降低聚类的总SSE。
如果有多个空簇，则该过程重复多次。

3–容易受到离群点的影响
使用平方误差时，离群点会过度影响所发现的簇
在可能的条件下，提前删除离群点
也可以在后处理时识别离群点

4–不能处理非球形簇、不同尺寸和不同密度的簇

2）k-中心点聚类方法

k-均值算法对离群点很敏感!

• 因为具有特别大的值的对象可能显著地影响数据的均值.

k-中心点(k-Medoids)：距离质心最近的点

• 不采用簇中对象的平均值作为参照点, 而是选用簇中最靠近中心的对象, 即中心点(medoid)作为参照点.。
  

三、凝聚层次聚类

层次聚类
将数据对象以树状的层次关系来看待。依层次建构的方式，一般分成两种来进行：凝聚的 、分裂的

• 凝聚的: 从点作为个体簇开始，每一步合并两个最接近的簇，直到只剩下一个簇
• 分裂的: 从包含所以点的某个簇开始，每一步分裂一个簇，直到只剩下单点簇

传统的层次聚类算法使用形似性矩阵或聚类矩阵；每次合并或分裂一个簇

1）基本的凝聚层次聚类算法

基本算法流程

关键操作是如何计算簇之间的邻近性

2）如何计算簇之间的邻近性

簇相似性: MIN or Single Link
单链，又称最短距离法，两个簇的邻近度定义为两个不同簇中任意两点之间的最短距离。

簇相似性: MAX or Complete Linkage
全链，又称最长距离法，两个簇的邻近度定义为两个不同簇中任意两点之间的最长距离。

簇相似性: Group Average
组平均法，两个簇的邻近度定义为两个不同簇中所有点对邻近度的平均值。

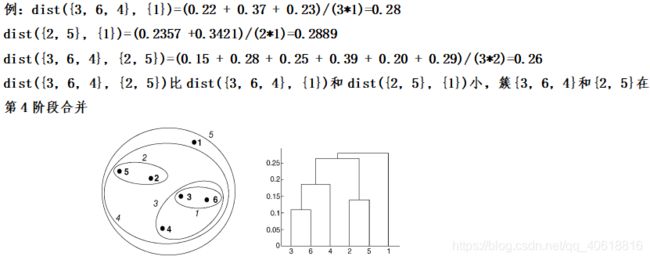
3）层次聚类的主要问题

• 缺乏全局目标函数。
  凝聚层次聚类不能视为全局优化一个目标函数。
• 处理不同大小的聚类能力。
  即如何处理待合并的簇对的相对大小。
  有两种方法：加权，平等的对待所有簇；非加权，考虑每个簇的点数。
• 合并决策是最终的。
  对于合并两个簇，凝聚层次算法倾向于作出好的局部决策，因为它们可以使用所有点的逐对相似度信息。然而，一旦作出合并两个簇的决策，以后就不能撤销。有一些技术试图克服“合并是最终的”这一限制。一种方法试图通过如下方法来修补层次聚类，移动树的分支以改善全局目标函数。另一种方法使用划分聚类技术（如K均值）来创建许多小簇，然后从这些小簇出发进行层次聚类。

bingo~   ✨ 只要心中花千树，人生何处不逢春。