乘幂法计算矩阵主特征值和特征向量-Matlab实现
文章目录
- 1.前言
- 2.方法介绍
- 3.算法步骤
- 4.数值实验
- 5.总结
- 6.Matlab代码
1.前言
乘幂法主要用于求实矩阵按模最大的特征值(主特征值)和相应特征向量.本文通过Matlab解决实际例子来验证乘幂法的正确性.
2.方法介绍
设实矩阵A的特征值为 λ 1 , λ 2 , . . . . . . , λ n \lambda_1,\lambda_2,......,\lambda_n λ1,λ2,......,λn,相应特征向量 x 1 , x 2 , . . . . . . , x n x_1,x_2,......,x_n x1,x2,......,xn线性无关.假设矩阵 A A A的特征值按模排序为 ∣ λ 1 ∣ ≥ ∣ λ 2 ∣ ≥ . . . ≥ ∣ λ n ∣ |\lambda_1|≥|\lambda_2|≥...≥|\lambda_n| ∣λ1∣≥∣λ2∣≥...≥∣λn∣,于是对任一非零向量 V ( 0 ) ∈ R n V^{(0)}∈R^n V(0)∈Rn可得到
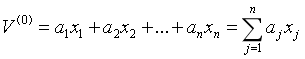 (1)
(1)
令
![]() (2)
(2)
可得向量序列:
 (3)
(3)
下面仅讨论 ∣ λ 1 ∣ > ∣ λ j ∣ , j = 2 , 3 , . . . , n . |\lambda_1|>|\lambda_j|,j=2,3,...,n. ∣λ1∣>∣λj∣,j=2,3,...,n.的情况:
由式(2)(3)知
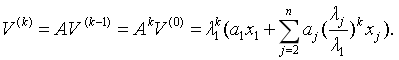 (4)
(4)
若 a ≠ 0 , a≠0, a=0,则当 k k k充分大时有
![]() (5)
(5)
显然当 k k k充分大时,由 ∣ λ j λ 1 ∣ k → 0 |\frac{\lambda_j}{\lambda_1}|^k→0 ∣λ1λj∣k→0知 ϵ k → 0 \epsilon_k→0 ϵk→0.由于特征向量可以相差一个倍数,故式(5)表明 V ( k ) V^{(k)} V(k)就是相应于 λ 1 \lambda_1 λ1的近似特征向量.而对 λ 1 \lambda_1 λ1,由(5)可看出,若 V 1 ( k ) V_1^{(k)} V1(k)用表示的第1个分量,则
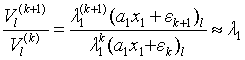 (6)
(6)
具体计算时 V ( 0 ) V^{(0)} V(0)的选取很难保证一定有 a 1 ≠ 0 a_1≠0 a1=0.但由于舍入误差的影响,只要迭代次数足够多就会有 a 1 ′ ≠ 0 a_1'≠0 a1′=0,因而最后的结论成立.
以上讨论说明了乘幂法的基本原理.当 λ 1 \lambda_1 λ1过大或过小时都会导致 ∣ ∣ V ( k ) ∣ ∣ ||V^{(k)}|| ∣∣V(k)∣∣过大或过小,以致运算无法继续.因此实际计算时需作规范化运算:
任取 V ( 0 ) ∈ R n , V ( 0 ) ≠ 0 V^{(0)}∈R^n,V^{(0)}≠0 V(0)∈Rn,V(0)=0,令 U ( 0 ) = V ( 0 ) U^{(0)}=V^{(0)} U(0)=V(0),按下列公式反复计算:
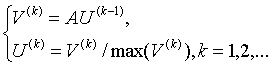 (7)
(7)
这里 m a x ( V ) max(V) max(V)表示向量 V V V的按模最大的分量对于规范化乘幂法,有如下收敛性定理.
定理:设 A A A为 n × n n×n n×n实矩阵,其特征值满足 ∣ λ 1 ∣ ≥ ∣ λ 2 ∣ ≥ . . . ≥ ∣ λ n ∣ |\lambda_1|≥|\lambda_2|≥...≥|\lambda_n| ∣λ1∣≥∣λ2∣≥...≥∣λn∣,向量序列 ( U ( k ) , V ( k ) ) ({U^{(k)},V^{(k)}}) (U(k),V(k))由式(7)确定,则 m a x ( V ( k ) ) → λ 1 , U ( k ) → x 1 / m a x ( x 1 ) ( k → ∞ ) max(V^{(k)})→\lambda_1,U^{(k)}→x_1/max(x_1) (k→∞) max(V(k))→λ1,U(k)→x1/max(x1)(k→∞).
定理证明从略.
3.算法步骤
先判断矩阵主特征值是否可用乘幂法计算,判断思路见代码注释.
给定误差限 ϵ \epsilon ϵ和最大迭代次数 m m m,任取 V ( 0 ) ∈ R n , V ( 0 ) ≠ 0 V^{(0)}∈R^n,V^{(0)}≠0 V(0)∈Rn,V(0)=0,令 U ( 0 ) = V ( 0 ) U^{(0)}=V^{(0)} U(0)=V(0),按下列公式反复计算:
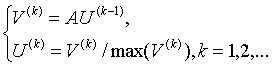 (8)
(8)
这里 m a x ( V ) max(V) max(V)表示向量 V V V的按模最大的分量对于规范化乘幂法. 最终有![]()
当达到 ∣ m a x ( V ( k + 1 ) ) − m a x ( V ( k ) ) ∣ |max(V^{(k+1)})-max(V^{(k)})| ∣max(V(k+1))−max(V(k))∣或 k = m k=m k=m时停止迭代, m a x ( V ( k ) ) max(V^{(k)}) max(V(k))即为主特征值 λ 1 \lambda_1 λ1的近似值, ( U ( k ) ) T (U^{(k)})^T (U(k))T即为对应的特征向量.
注意:取V的按模最大分量而非最大分量,否则运算结果出错.
4.数值实验
下面通过一道例题验证上述求解矩阵特征值问题方法的正确性和可行性.
例:求矩阵
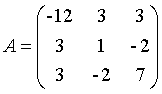
的特征值和特征向量,并对照标准答案.
标准答案: A A A的特征值 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3分别为 -13.220179976292638 ,1.391318328272217 ,7.828861648020419,对应的特征向量 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3分别为![]()
![]()
![]()
解:乘幂法求主特征值和特征向量.
取 V ( 0 ) = U ( 0 ) = ( 1 , 1 , 1 ) T V^{(0)}=U^{(0)}=(1 ,1 ,1)^T V(0)=U(0)=(1,1,1)T,计算结果见下表,收敛标准为 ∣ m a x ( V ( k + 1 ) ) − m a x ( V ( k ) ) ∣ < ϵ = 1 0 6 |max(V^{(k+1)})-max(V^{(k)})|<\epsilon=10^6 ∣max(V(k+1))−max(V(k))∣<ϵ=106.
| k k k | ( V ( k ) ) T (V^{(k)})^T (V(k))T | ( U ( K ) ) T (U^{(K)})^T (U(K))T | m a x ( V ( k ) ) max(V^{(k)}) max(V(k)) |
|---|---|---|---|
| 0 | [1 1 1] | [1 1 1] | 1 |
| 1 | [ -6.0, 2.0, 8.0] | [ -0.75, 0.25, 1.0] | 8.00000000 |
| 2 | [ 12.75, -4.0, 4.25] | [ 1.0, -0.31372549, 0.333333333] | 12.75000000 |
| 3 | [ -11.9411765, 2.01960784, 5.96078431] | [ 1.0, -0.169129721, -0.499178982] | -11.94117647 |
| … | … | … | … |
| 31 | [ -13.2201794, 3.10813636, 2.26886445] | [ 1.0, -0.235105459, -0.171621305] | -13.22017944 |
| 32 | [ -13.2201803, 3.10813715, 2.26886178] | [ 1.0, -0.235105504, -0.171621092] | -13.22018029 |
所以主特征值近似值为-13.22018029,对应特征向量为 [ 1.0 , − 0.235105504 , − 0.171621092 ] T [1.0,-0.235105504,-0.171621092]^T [1.0,−0.235105504,−0.171621092]T.
5.总结
从以上数值结果来看,对照问题的真实解可以看出,乘幂法能在较少的步数内很好地求解其适用范围内的矩阵特征值问题.通过这次数值实验,我们验证乘幂法是正确的,对于求解一定的矩阵特征值问题是有效的.
6.Matlab代码
1.判读是否可用乘幂法的函数
function [lambdaa,beta]=power_method_judge_HYH(A)
%功能:此函数用于A能否使用乘幂法
%其中lambdaa,beta是实际的特征值及其对应的特征向量
%A是待求矩阵,times,x0,ep分别为最大迭代次数,初始向量,误差
%原理:若特征值非单根,主特征值为重根,此时对应于主特征值的特征向量子空间可能不是一维的...
%...这样不同的初始向量可能得到线性无关的特征向量
format long;
b=eig(A); %A中的全部特征值存到向量b中
c=size(b); %b的元素个数存到c中
d=c(1)*c(2); %特征值的总个数
e=length(unique(b)); %不考虑重复的特征值个数
if(d==e)
fprintf('特征值互异,矩阵可对角\n');
fprintf('请选择使用的方法\n');
else
error('特征值有重复,矩阵不可对角化\n');
end
2.乘幂法
function[lambda,x]=power_method_cal_HYH(A,times,x0,e)
%乘幂法
%其中lambda,x是得出的特征值及其对应的特征向量
%A是待求矩阵,times,x0,e分别为最大迭代次数,初始向量,误差
clc;
digits(9);
k=1;
u=0; %u用来记录上一次循环得到的alpha
[m,n]=size(x0);
y=zeros(m,n);
y=x0; %y为初始向量
while k<=times
x=A*y;
z=abs(x); %z存储x各元素的绝对值
[m,p]=max(z); %找出z大值及位置
lambda=x(p); %求x中按模最大的元素
y=x./lambda; %y最终趋于x/max(x)
fprintf('第%d次迭代\n',k);
fprintf('lambda=%.8f\n',lambda);
disp(vpa(x'));
disp(vpa(y'));
if abs(lambda-u)<e
break
else
k=k+1;
u=lambda;
end
end