第3章 Python 数字图像处理(DIP) - 灰度变换与空间滤波15 - 锐化高通滤波器 -拉普拉斯核(二阶导数)
目录
- 锐化(高通)空间滤波器
-
-
- 基础 - 一阶导数和二阶导数的锐化滤波器
- 二阶导数锐化图像--拉普拉斯
-
锐化(高通)空间滤波器
- 平滑通过称为低通滤波
- 类似于积分运算
- 锐化通常称为高通滤波
- 微分运算
- 高过(负责细节的)高频,衰减或抑制低频
基础 - 一阶导数和二阶导数的锐化滤波器
数字函数的导数是用差分来定义的。定义这些差分的方法有多种
一阶导数的任何定义都要满足如下要求:
- 恒定灰度区域的一阶导数必须为0
- 灰度台阶或斜坡开始处的一阶导数必须非零。
- 灰度斜坡上的一阶导数必须非零。
二阶导数的任何定义都要满足如下要求:
- 恒定灰度区域的二阶导数必须为零。
- 灰度台阶或斜坡的开始处和结束处的地阶导数必须非零。
- 灰度斜坡上的二阶导数必须为零。
一维函数 f ( x ) f(x) f(x)的一阶导数的一个基本定义是差分:
∂ f ∂ x = f ( x + 1 ) − f ( x ) (3.48) \frac{\partial f}{\partial x} = f(x+1) -f(x) \tag{3.48} ∂x∂f=f(x+1)−f(x)(3.48)
二阶导数定义为差分:
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) (3.49) \frac{\partial^2 f}{\partial x^2} = f(x+1) + f(x-1) - 2f(x) \tag{3.49} ∂x2∂2f=f(x+1)+f(x−1)−2f(x)(3.49)
def first_derivative(y):
y_1 = np.zeros(len(y)-1)
for i in range(1, len(y)):
if i + 1 < len(y):
y_1[i] = y[i+1] - y[i]
return y_1
def second_derivative(y):
y_2 = np.zeros(len(y)-1)
for i in range(1, len(y)):
if i + 1 < len(y):
y_2[i] = y[i+1] + y[i-1] - 2*y[i]
return y_2
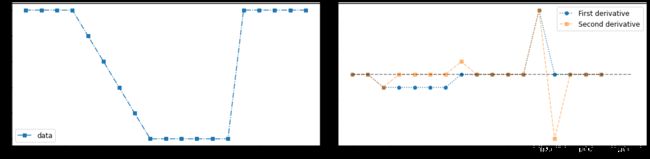
#一维数字一阶与二阶导数
y = np.arange(1, 7)
y = y[::-1]
y = np.pad(y, (3, 5), mode='constant', constant_values=(6, 1))
y = np.pad(y, (0, 5), mode='constant', constant_values=(0, 6))
x = np.arange(len(y))
fig = plt.figure(figsize=(16, 4))
ax_1 = fig.add_subplot(1, 2, 1)
ax_1.plot(x, y, '-.s', label="data")
ax_1.legend(loc='best', fontsize=12)
y_1 = first_derivative(y)
y_2 = second_derivative(y)
ax_2 = fig.add_subplot(1, 2, 2)
ax_2.plot(y_1[1:], ':o', label='First derivative')
ax_2.plot(y_2[1:], '--s', alpha=0.5, label='Second derivative')
ax_2.plot(np.zeros(19), '--k', alpha=0.5)
ax_2.legend(loc='best', fontsize=12)
plt.tight_layout()
plt.show()
二阶导数锐化图像–拉普拉斯
我们感兴趣的是各向同性核,这种核的响应与图像中灰度不连续的方向无关。最简单的各向同性导数算子(核)是拉普拉斯, 它定义为:
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 (3.50) \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \tag{3.50} ∇2f=∂x2∂2f+∂y2∂2f(3.50)
我们把这个片子以离散形式表达:
∂ 2 f ∂ x 2 = f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) (3.51) \frac{\partial^2 f}{\partial x^2} = f(x+1, y) + f(x-1, y) -2f(x, y) \tag{3.51} ∂x2∂2f=f(x+1,y)+f(x−1,y)−2f(x,y)(3.51)
∂ 2 f ∂ y 2 = f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) (3.52) \frac{\partial^2 f}{\partial y^2} = f(x, y+1) + f(x, y-1) -2f(x, y) \tag{3.52} ∂y2∂2f=f(x,y+1)+f(x,y−1)−2f(x,y)(3.52)
两个变量的离散拉普拉斯是
∇ 2 f ( x , y ) = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) (3.53) \nabla^2 f(x, y)= f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1)-4f(x, y) \tag{3.53} ∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)(3.53)
写成矩阵的形式就得到拉普拉斯核:
[ 0 1 ( f ( x , y − 1 ) 的 权 值 ) 0 1 ( f ( x − 1 , y ) 的 权 值 ) − 4 ( f ( x , y ) 的 权 值 ) 1 ( f ( x + 1 , y ) 的 权 值 ) 0 1 ( f ( x , y + 1 ) 的 权 值 ) 0 ] \begin{bmatrix} 0 & 1 (f(x,y-1)的权值) & 0 \\ 1 (f(x-1,y)的权值) & -4 (f(x,y)的权值) & 1 (f(x+1,y)的权值) \\ 0 & 1 (f(x,y+1)的权值) & 0\end{bmatrix} ⎣⎡01(f(x−1,y)的权值)01(f(x,y−1)的权值)−4(f(x,y)的权值)1(f(x,y+1)的权值)01(f(x+1,y)的权值)0⎦⎤
图像的锐化的滤波原理也类似于描述的低通滤波,只不过使用不同的系数
后面两个是含对角项的扩展公式的核:
[ 0 1 0 1 − 4 1 0 1 0 ] [ 1 1 1 1 − 8 1 1 1 1 ] \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1\end{bmatrix} ⎣⎡0101−41010⎦⎤⎣⎡1111−81111⎦⎤
这两个是二阶导数定义得到的:
[ 0 − 1 0 − 1 4 − 1 0 − 1 0 ] [ − 1 − 1 − 1 − 1 8 − 1 − 1 − 1 − 1 ] \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0\end{bmatrix} \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1\end{bmatrix} ⎣⎡0−10−14−10−10⎦⎤⎣⎡−1−1−1−18−1−1−1−1⎦⎤
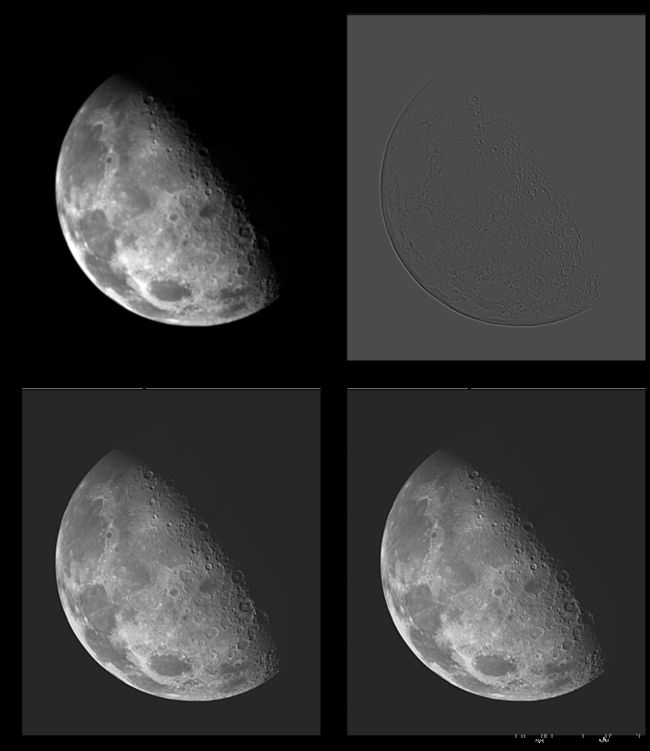
拉普拉斯是导数算子,因此会突出图像中的急剧灰度过渡,并且不会强调缓慢变化的灰度区域。这往往会产生具有灰色边缘线和其他不连续性的图像,它们都叠加在暗色无特征背景上。将拉普拉斯图像与原图相加,就可以“恢复”背景特征,同时保留拉普拉斯的锐化效果。 上面两个核得到的图像需要用原图减去得到的图,下面两个核得到的图像需要用原图加下得到的图,以实现锐化。
g ( x , y ) = f ( x , y ) + c [ ∇ 2 f ( x , y ) ] (3.54) g(x,y) = f(x,y) + c[\nabla^2 f(x,y)] \tag{3.54} g(x,y)=f(x,y)+c[∇2f(x,y)](3.54)
使用上面的前两个核,则 c = − 1 c = -1 c=−1,后面的两个二阶导数定义的核则 c = 1 c = 1 c=1
两组核刚好相差一个负号
观察平滑与锐化核可发现,平滑核的系数之和为1,锐化核的系数之和为0。用锐化核处理图像时,有会出现负值,需要进行额外处理才能得到合适的视觉结果。
# Laplacian filter 不同的核,拉普拉斯锐化
img = cv2.imread('DIP_Figures/DIP3E_Original_Images_CH03/Fig0338(a)(blurry_moon).tif', 0)
img = normalize(img)
kernel_laplacian_a = np.array([
[0,1,0],
[1,-4,1],
[0,1,0]])
# 下面这个核虽然可以锐化,但是效果没有上面这个好
# kernel_laplacian_d = np.array([[
# [-1, -1, -1],
# [-1, 8, -1],
# [-1, -1, -1]
# ]])
laplacian_img_a = filter_2d(img, kernel_laplacian_a, mode='constant')
laplacian_img_b = filter_2d(img, -kernel_laplacian_a, mode='constant')
plt.figure(figsize=(14, 16))
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray', vmin=0, vmax=1), plt.title('Original')
plt.subplot(2, 2, 2), plt.imshow(laplacian_img_a, cmap='gray', vmax=1), plt.title('Laplacian')
laplacian_img_ori = normalize(img - laplacian_img_a)
plt.subplot(2, 2, 3), plt.imshow(laplacian_img_ori, cmap='gray', vmax=1), plt.title('Laplacian With ORI')
laplacian_imgori = normalize(img + laplacian_img_b)
plt.subplot(2, 2, 4), plt.imshow(laplacian_imgori, cmap='gray', vmax=1), plt.title('Laplacian With ORI')
plt.tight_layout()
plt.show()