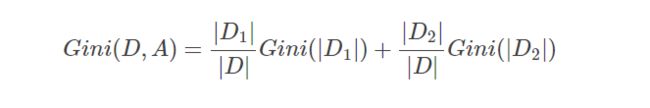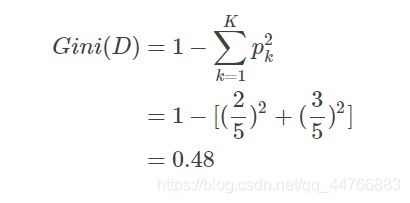熵，信息增益，信息增益率，基尼指数(附案例)

数据样例

名称	是否用鳃呼吸	有无鱼鳍	是否为鱼
鲨鱼	是	有	是
鲫鱼	是	有	是
河蚌	是	无	否
鲸	否	有	否
海豚	否	有	否

熵

熵(Entropy) 是度量样本集合纯度最常用的一种指标，对于包含m个训练样本的数据集D:{(X⁽¹⁾,y⁽¹⁾⁾,(X⁽²⁾,y⁽²⁾),⋯，(X^(m),y^(m))} ,在数据集D中，第k类的样本所占的比例为$p_k$,则数据集D的信息熵为：

$$Info(D)=-\sum _{i=1}^m{p}_{i}lo{g}_2(p_i)$$

其中，K表示的是数据集D中类别的个数。对于数据样例中的，是否为鱼这一结果。其信息熵为;

$$Info(D)=-\sum _{i=1}^2{p}_{i}lo{g}_2{p}_i=-\frac{2}{5}lo{g}_2\frac{2}{5}-\frac{3}{5}lo{g}_2\frac{3}{5}=0.971$$

当样本按照特征A的值a划分成两个独立的子数据集 $D_1和D_2$时，此时整个数据集D的熵分为两个独立数据集 $D_1$的熵和 $D_2$的熵的加权和，即：

$$\begin{array}{rl}Inf{o}_A(D)& =\sum _{j=1}^2\frac{|D_j|}{|D|}\times Info(D)\\ & =-\frac{|D_1|}{|D|}\sum _{k=1}^K{p}_{k}lo{g}_2{p}_k-\frac{|D_2|}{|D|}\sum _{k=1}^K{p}_{k}lo{g}_2{p}_k\end{array}$$

其中， $|D_1|$表示的是数据集$|D_1|$中的样本的个数， $|D_2|$表示的是数据集 $|D_2|$中的样本的个数。对于数据样例，将样本按照特征“是否用鳃呼吸”划分成两个独立的子数据集，此时，数据集D的信息熵为：

$$\begin{array}{rl}Inf{o}_A(D)& =\frac{3}{5}Info(D_1)+\frac{2}{5}Info(D_2)\\ & =-\frac{3}{5}(\frac{2}{3}lo{g}_2\frac{2}{3}+\frac{1}{3}lo{g}_2\frac{1}{3})-\frac{2}{5}lo{g}_{2}1\\ & =0.551\end{array}$$

信息增益

由上述的划分可以看出，在划分后的数据集D的信息熵减小了，对于给定的数据集，划分前后信息熵的减少量称为 信息增益(information gain)，就是原来的信息需求与新的信息需求的差。即：

$$Gain(A)=Info(D)-Inf{o}_A(D)$$

信息熵表示的数据集中的不纯度，信息熵较小表明数据集纯度提升了。在选择数据集划分的标准时，通常选择能够使的信息增益最大的划分。ID3决策树算法就是利用信息增益作为划分数据集的一种方法。数据样例中，

$$Gain{(}^{\prime }是否用鳃呼{吸}^{\prime })=Info(D)-Inf{o}_A(D)=0.971-0.551=0.44$$

缺陷：该方法倾向于选择具有大量值的属性。例如，按id分组，此时每个分区值包含一个元组，由于每个分区都是纯的，所以基于该划分对数据集D分类所需要的信息为$inf{o}_{id}(D)=0$。因此通过对该属性的划分得到的信息增益最大。显然，这种划分对分类没用。

信息增益率

在上面，我们提到了ID3使用信息增益进行判断的缺陷，那么如何改进呢？

ID3的后继C4.5使用一种称为 增益率（Gain Ratio) 的信息增益扩充，试图克服这种偏依。它用 分裂信息(split information) 值将信息增益规范化，如下：

$$SplitInf{o}_A(D)=-\sum _{j=1}^v\frac{|D_j|}{D}\times lo{g}_2(\frac{|D_j|}{|D|})$$

增益率定义为：

$$GrianRate(A)=\frac{Grain(A)}{SplitInf{o}_A(D)}$$

此时如果分类以id进行，不难看出我们的SplitInfo也会很大，这样就会对我们求得的结果进行一个矫正，避免出现极端情况。

在数据样例中，是否用鳃呼吸作为特征A，其 SplitInfo_A(D) 为：

$$\begin{array}{rl}SplitInf{o}_A(D)& =-\sum _{j=1}^v\frac{|D_j|}{D}\times lo{g}_2(\frac{|D_j|}{|D|})\\ & =-\frac{3}{5}lo{g}_2\frac{3}{5}-\frac{2}{5}lo{g}_2\frac{2}{5}\\ & =0.971\end{array}$$

信息增益率为：

$$\begin{array}{rl}GrianRate(A)& =\frac{Grain(A)}{SplitInf{o}_A(D)}\\ & =\frac{0.971}{0.44}\\ & =2.0682\end{array}$$

基尼指数

无论是ID3还是C4.5，都是基于熵的模型，里面会涉及到大量的对数运算，能不能简化一下？

CART中采用基尼指数来进行特征选择

基尼指数（Gini index)也可以选择最优的划分属性，对于数据集D，假设有K个分类，则样本属于第k个类的概率为pk则此概率分布的基尼系数为：

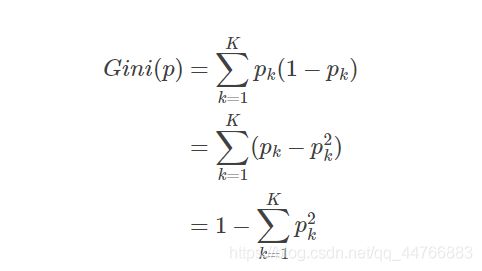
对于数据集D，其基尼指数为：
其中，$|C_k|$表示数据集D中，属于类别 k的样本的个数。若此时根据特征A将数据集D划分为独立的两个数据集D1和 D2，此时的基尼指数为:

在数据样例中，数据集D的基尼指数（针对是否为鱼而言）:

利用特征“是否用鳃呼吸”将数据集D划分成独立的两个数据集 D1和 D2后，其基尼指数为：

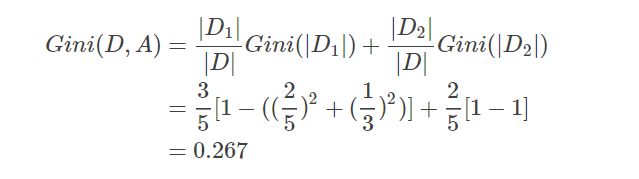
参考：

• 熵、信息增益、信息增益率与基尼指数
• 数据挖掘概念与技术 Jiawei Han Jian Pei