卡尔曼滤波-建立卡尔曼滤波直觉
卡尔曼滤波-建立卡尔曼滤波直觉
- 概述
-
- 预测算法的必要性
- 数学知识
-
-
- 均值和期望值
- 方差和标准差
-
- 拓展一下(有偏估计和无偏估计)
- 高斯分布(正态分布)
- 随机变量
- 估计、准确度和精度
- 小结
-
- α−β−γ 滤波
-
- 例1:称金条的重量
- 称金条中蕴含的卡尔曼滤波的思想(必看)
-
- 下面重点来了,只要看完了下面的推导过程,你就会理解卡尔曼滤波的思想了,建立起卡尔曼滤波的直觉
- 那么为什么这里的卡尔曼增益会等于 1 n \frac{1}{n} n1呢?
-
- 算法估计流程图
概述
卡尔曼滤波作为一种强大的数据融合和数据预测算法,在很多方面都有着不错的运用;用于雷达追踪定位和导航系统、控制系统、计算机图形等等。
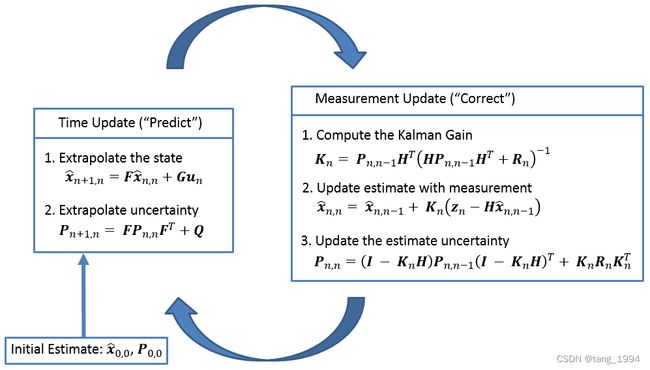
卡尔曼滤波的核心思想比较简单,核心就是下面图一中的五个公式,更新和预测不停的迭代下去,但是许多书籍和教程并不容易理解。
大多数教程都默认读者具备了相应的数学背景(虽然我认为确实是的,但是上来就怼公式真的很难学进去),把公式晾出来之后,就开始推导,我反正很难看进去,而且大都缺乏实用的数值示例让读者更进一步的从实际角度去理解。所以造成的结果就是每一个公式都看得懂,组合起来就懵逼的那种。
所以这里我会先帮助大家建立起一种“直觉”,对于卡尔曼滤波算法的直觉,让您能够深入的理解它的原理,再加上实际的数值例子来加深您的直觉,这样就不用今天死记公式,几天后又给忘了,从底层原理去理解它,能够帮助大家更久更好的记住它。
预测算法的必要性
再深入了解卡尔曼滤波之前,我们先来考虑一个雷达追踪的场景:

假设一个追踪周期为5秒。跟踪雷达向目标方向发送一束射束。也就是每5秒,雷达就会通过向目标方向发送专用跟踪波束来重新定位目标。
发送波束后,雷达估计当前目标位置和速度。并且雷达还估计(或预测)下一个发射跟踪波束的目标位置。
可以使用牛顿运动方程轻松计算未来目标位置:
x = x 0 + v 0 Δ t + 1 2 a Δ t 2 x 是目标的位置 x 0 是初始的位置 v 0 是初始的速度 a 是目标的加速度 Δ t 是时间间隔(这里是 5 s ) x=x_0+v_0\Delta t+\frac{1}{2}a\Delta t^2 \\ x是目标的位置\\ x_0是初始的位置\\ v_0是初始的速度\\ a是目标的加速度\\ \Delta t是时间间隔(这里是5s) x=x0+v0Δt+21aΔt2x是目标的位置x0是初始的位置v0是初始的速度a是目标的加速度Δt是时间间隔(这里是5s)
而在三维空间中,上面的牛顿公式可以重写成下面这种:
x = x 0 + v x 0 Δ t + 1 2 a x Δ t 2 y = y 0 + v y 0 Δ t + 1 2 a y Δ t 2 z = z 0 + v z 0 Δ t + 1 2 a z Δ t 2 x=x_0+v_{x0}\Delta t+\frac{1}{2}a_x\Delta t^2 \\ y=y_0+v_{y0}\Delta t+\frac{1}{2}a_y\Delta t^2 \\ z=z_0+v_{z0}\Delta t+\frac{1}{2}a_z\Delta t^2 \\ x=x0+vx0Δt+21axΔt2y=y0+vy0Δt+21ayΔt2z=z0+vz0Δt+21azΔt2
上面的公式被称为状态空间模型(Dynamic model),它描述的是输入状态和输出状态之间的关系。
其中 [ x , y , z , v x , v y , v z , a x , a y , a z ] [x,y,z,v_x,v_y,v_z,a_x,a_y,a_z] [x,y,z,vx,vy,vz,ax,ay,az]也就是我们常说的系统状态,在算法预测阶段(predict),输入是当前的状态,输出是下个时间节点的状态。
根据上面给出的公式可以知道,当我们知道状态空间模型和当前的状态的时候,可以很容易的预测出模型下一个时间点的状态。
然而事实并非如此。首先,雷达测量不是绝对准确的。它包括随机误差(或者称为不确定性)。误差幅度取决于许多参数,例如雷达校准、波束宽度和返回回波的信噪比。测量中包含的误差称为测量噪声。
此外,由于风、空气湍流和飞行员机动等外部因素,目标运动并不严格符合运动方程。动态模型误差(或不确定性)称为过程噪声。
由于测量噪声和过程噪声,估计的目标位置可能与实际目标位置相距甚远。在这种情况下,雷达可能会向错误的方向发送跟踪波束而错过目标。
所以我们需要一种考虑过程和测量不确定性的预测算法来提高雷达跟踪性能。
最广泛使用的预测算法是卡尔曼滤波器。
数学知识
几个基本术语,方差、标准差、正态分布、估计值、准确度、精确度(精度)、均值、期望值和随机变量
我相信有精力学习卡尔曼滤波的读者,基本上对这部分数学知识都是很清楚的,没兴趣的读者可以直接跳过,有兴趣的读者可以当作复习一下吧;不过就算是不大清楚这部分数学知识的读者,我也会尽量让大家都看懂。
均值和期望值
E 期望值 μ 均值 E期望值\\ \mu均值 E期望值μ均值
均值和期望值是两个密切相关的数学术语,很多情况下我们都是直接使用均值等于期望值,如下图公式,但是他们确实存在区别。
E ( x ) = μ E(x)=\mu E(x)=μ
例如,我们有两个五美分和三个十美分的硬币,我们可以很容易的计算他们的均值。

V m e a n = 1 N ∑ n = 1 N V n = 1 5 ( 5 + 5 + 10 + 10 + 10 ) = 8 c e n t V_{mean}=\frac{1}{N}\sum_{n=1}^N{V_n}=\frac{1}{5}(5+5+10+10+10)=8cent Vmean=N1n=1∑NVn=51(5+5+10+10+10)=8cent
上面这个例子中,输出结果不能定义为预期值,因为系统状态(硬币值)没有隐藏,我们使用了整个族群(所有5个硬币)来计算平均值,所以这里均值不能被称为期望值。
现在假设同一个人测出了五个不同的体重值:79.8kg、80kg、80.1kg、79.8kg和80.2kg;一个人可以看作一个系统,人的体重可以看作是一个系统状态。

这五次的测量值之所以不一样是因为体重秤在测量时存在一个随机误差,由于人的体重它是一个隐藏状态所以我们不知道人的真实体重。但是我们可以通过求这五次测量值的均值来估计人的体重。估计的结果是人体重的期望值。
期望值就是您期望隐藏变量在很长一段时间或多次试验中具有的值。
方差和标准差
方差是衡量数据集偏离均值的程度,标准差是方差的平方根,一般标准差用希腊字母 σ = 1 N ∑ n = 1 N ( x n − μ ) 2 \sigma=\sqrt{\frac{1}{N}\sum_{n=1}^N(x_n-\mu)^2} σ=N1n=1∑N(xn−μ)2表示,方差则是 σ 2 = 1 N ∑ n = 1 N ( x n − μ ) 2 \sigma^2=\frac{1}{N}\sum_{n=1}^N(x_n-\mu)^2 σ2=N1n=1∑N(xn−μ)2表示。
我们就下面两个学校的篮球队队员的身高来进行比较吧。
| 球员1 | 球员2 | 球员3 | 球员4 | 球员5 | 平均身高 | |
|---|---|---|---|---|---|---|
| A队 | 1.89m | 2.1m | 1.75m | 1.98m | 1.85m | 1.914m |
| B队 | 1.94m | 1.9m | 1.97m | 1.89m | 1.87m | 1.914m |
根据方差公式,就是每个队的身高与他们的身高均值的差值的平方和再求均值。
最终分别求得球队A和B的方差如下:
σ A 2 = 1 N ∑ n = 1 N ( x A n − μ A ) 2 = 1 5 ( 0.000576 + 0.034596 + 0.026896 + 0.004356 + 0.004096 ) = 0.014 m 2 σ B 2 = 1 N ∑ n = 1 N ( x B n − μ B ) 2 = 1 5 ( 0.000676 + 0.000196 + 0.003136 + 0.000576 + 0.001936 ) = 0.0013 m 2 \sigma^2_A=\frac{1}{N}\sum_{n=1}^N(x_{An}-\mu_A)^2=\frac{1}{5}(0.000576+0.034596+0.026896+0.004356+0.004096)=0.014m^2\\ \sigma^2_B=\frac{1}{N}\sum_{n=1}^N(x_{Bn}-\mu_B)^2=\frac{1}{5}(0.000676+0.000196+0.003136+0.000576+0.001936)=0.0013m^2 σA2=N1n=1∑N(xAn−μA)2=51(0.000576+0.034596+0.026896+0.004356+0.004096)=0.014m2σB2=N1n=1∑N(xBn−μB)2=51(0.000676+0.000196+0.003136+0.000576+0.001936)=0.0013m2
A队的标准差为 0.12 m = σ A 2 = 0.014 m 2 0.12m=\sqrt{\sigma_A^2}=\sqrt{0.014m^2} 0.12m=σA2=0.014m2
B队的标准差为 0.036 m = σ B 2 = 0.0013 m 2 0.036m=\sqrt{\sigma_B^2}=\sqrt{0.0013m^2} 0.036m=σB2=0.0013m2
从标准差或者方差可以看到,A和B两队的平均身高一样,但是A队身高的多样性更多,从篮球的角度考虑A队身高分布更合理,因为中锋,前锋,后卫的身高是相差比较大的,而B队的身高从篮球的角度来看不大合理,身高差别不大。
拓展一下(有偏估计和无偏估计)
假设我们要计算所有高中所有篮球运动员身高的均值和方差。
这将是一项艰巨的任务,因为我们需要收集每所高中每位球员的身高数据。
所以一般我们可以通过抽样出一个大数据集并在这个数据集上进行计算来估计玩家的均值和方差,从而降低这项任务的工作量。也就是我们常说的抽样调查,所以上面的大数据集抽样要尽可能的多样,尽可能的随机,从而保证评估效果的准确性。
均值估计公式 μ = μ s a m p l e = 1 N ∑ n = 1 N H s a m p l e n \mu=\mu_{sample}=\frac{1}{N}\sum_{n=1}^{N}H_{sample_n} μ=μsample=N1n=1∑NHsamplen属于无偏估计。
然而,当我们估计方差时,方差计算的方程式略有不同。不是按照样本的个数N归一化,我们将通过样本数N-1归一化 ,也就是我们通常说的有偏估计:
σ 2 = N N − 1 σ s a m p l e 2 = 1 N − 1 ∑ n = 1 N ( x A n − μ s a m p l e ) 2 \sigma^2=\frac{N}{N-1}\sigma^2_{sample}=\frac{1}{N-1}\sum_{n=1}^N(x_{An}-\mu_{sample})^2 σ2=N−1Nσsample2=N−11n=1∑N(xAn−μsample)2
至于为啥一个是有偏一个是无偏,这里就不拓展,有兴趣的读者可能查阅资料。
高斯分布(正态分布)
高斯分布是数学课程中很重要的一课,以伟大的数学家高斯名字命名,很多的自然现象都遵循着高斯分布,所以在很多场景都用到过高斯分布,在很多问题上面进行建模,都会用到高斯分布。而且高斯公式的简洁性让它的地位更加稳固,他只需要一个均值和一个方差就可以表达出他的公式。 F ( x ; μ , σ ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 F(x;\mu,\sigma)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}} F(x;μ,σ)=2πσ1e2σ2−(x−μ)2
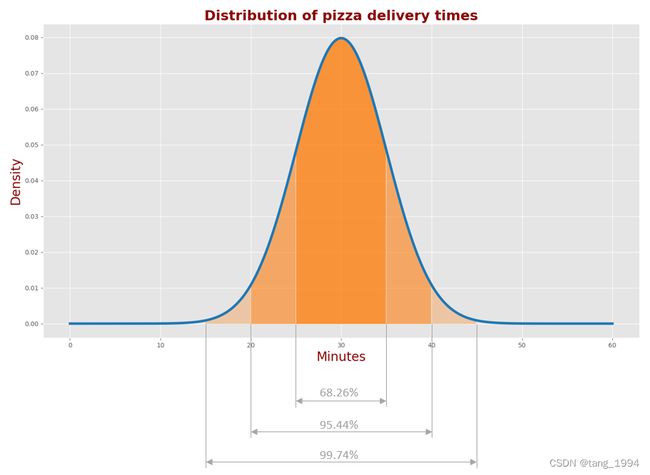
高斯曲线也称为正态分布的概率密度函数 (PDF)。
下图描述了三个城市的披萨配送时间的 PDF:城市“A”、城市“B”和城市“C”。

- 在“A”城市,平均送货时间为 30 分钟,标准差为 5 分钟。
- 在城市“B”,平均送货时间为 40 分钟,标准差为 5 分钟。
- 在城市“C”,平均送货时间为 30 分钟,标准差为 10 分钟。
我们可以看到城市“A”和城市“B”的披萨配送时间的高斯形状是相同的;但是,它们的中心不同也就是平均时间不同。这意味着在城市“A”,您等待比萨饼的平均时间减少了 10 分钟,而比萨交付时间的分散度是相同的。
我们还可以看到城市“A”和城市“C”的高斯中心是相同的;但是,它们的形状不同。因此,两个城市的平均比萨送货时间相同,但配送的时间分布不同。
- 68.26% 的交货时间在μ ± σ范围(25-35 分钟)
- 95.44% 的交货时间在 μ ± 2 σ 范围(20-40 分钟)
- 99.74% 的交货时间在 μ ± 3 σ 范围(15-45 分钟)
通常,测量误差呈正态分布。卡尔曼滤波器设计的时候也假定测量误差服从正态分布。
随机变量
随机变量X描述了系统的隐藏状态。随机变量是来自随机实验的一组可能值。随机变量可以是连续的或离散的:
- 连续随机变量可以取特定范围内的任何值,例如电池充电时间或马拉松比赛时间。
- 离散随机变量是可数的,例如网站访问者的数量或班级中的学生人数。
在卡尔曼滤波里面只用到了随机变量X的两个性质:均值和方差
估计、准确度和精度
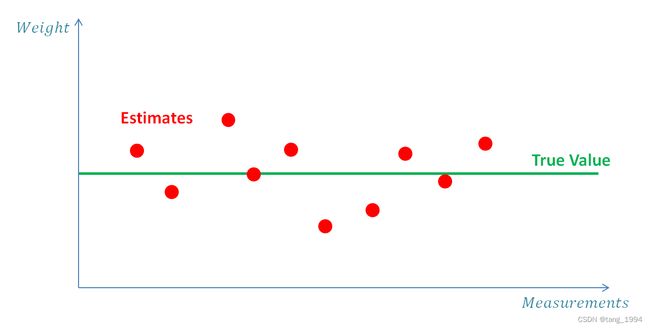
估计是评估系统中的隐藏状态。飞机的真实位置对观察者是隐藏的或者说未知的。我们可以使用雷达等传感器来估计飞机的位置。通过使用多个传感器并应用高级估计和跟踪算法(例如卡尔曼滤波器),可以显着改善估计。每个测量或计算的参数都是一个估计值。
准确度表示测量值与真值的接近程度。
精度描述了同一参数的一系列测量中的稳定性(或者说可变形)。准确度和精密度构成估算的基础。
下图说明了什么是准确度和精度:

高精度(High precision)系统在其测量中具有低方差(即低不确定性),而低精度(low precision)系统在其测量中具有高方差(即高不确定性)。随机测量中的误差产生方差。
低准确度(Low accuracy)系统被称为有偏差系统,因为它们的测量具有内置的系统误差(偏差),如上图左子图和中子图。
通过平均或平滑测量可以显着降低方差的影响。例如,如果我们使用具有随机测量误差的温度计测量温度,我们可以进行多次测量并取平均值。由于误差是随机的,一些测量值会高于真实值,而另一些会低于真实值。估计值将接近真实值。我们进行的测量越多,估计就越接近。
另一方面,有偏差的温度计会在估计中产生恒定的系统误差。
本教程中的所有示例都假设系统是无偏的。
小结
一次测量是一个随机变量,由概率密度函数 (PDF)描述。
所有测量的平均值是随机变量的期望值(Expected Value E(x))。
测量平均值与真实值之间的偏差就是测量的准确性(accuracy of the measurements),也称为偏差(bias)或系统测量误差。
离散度分布就是测量精度(measurement precision),也称为测量噪声、随机测量误差或测量不确定度(measurement uncertainty)。
α−β−γ 滤波
例1:称金条的重量
现在我们进入第一个简单的例子。在这个例子中,我们估计静态系统的状态。静态系统是在合理的时间内不会改变其状态的系统。例如,静态系统可以是一座塔,状态就是它的高度。
在这个例子中,我们估计金条的重量。我们有无偏尺度(可以回顾数学知识小结的篇章,里面有提到什么是有偏的测量),即测量没有系统误差,但测量确实包括随机噪声。
系统就是金条,系统状态就是金条的重量。系统的动态模型是恒定的或者静态的,因为我们假设权重不会在短期内发生变化。为了估计系统状态(即重量),我们可以进行多次测量并取平均值,从而消除随机噪声带来的影响。
在时间点n或者第n次测量之后,估计值 x ^ n n \hat x_{nn} x^nn表示前面所有测量结果的平均值。
x ^ n , n = 1 n ( z 1 + z 2 + z 3 + . . . + z n ) = 1 n ∑ i = 1 n z i \hat x_{n,n}=\frac{1}{n}(z_1+z_2+z_3+...+z_n)=\frac{1}{n}\sum_{i=1}^n{z_i} x^n,n=n1(z1+z2+z3+...+zn)=n1i=1∑nzi
上述参数的含义:
x x x 金条的真实重量
z n z_n zn 第n个时间点或者第n次测量的金条的重量
x ^ n , n \hat x_{n,n} x^n,n 在时间点n或者第n次测量之后,对金条评估的重量
x ^ n + 1 , n \hat x_{n+1,n} x^n+1,n在时间点n或者第n次测量之后预测n+1时间点金条的重量(这里的预测一般按照动态模型进行预测,也称为状态转移模型进行状态转移)
由于我们前面假设我们的动态模型是常态的和静态的,金条的重量不随时间的变化而变化,因此在进行状态转移的时候系统状态(金条重量)保持不变,也就是预测下个时间点的状态直接相等就可以了(也可以简单的理解成状态转移矩阵就是1)
所以 x ^ n + 1 , n \hat x_{n+1,n} x^n+1,n=1* x ^ n , n \hat x_{n,n} x^n,n
虽然上面的等式在数学上是正确的,但实现起来可行性不大。为了估计状态X̂ 我们需要记住所有历史测量值;因此,我们需要大内存。如果我们想在每次新测量后更新估计值,我们还需要反复重新计算平均值。因此,在数据量特别大的时候,计算会变得越来越困难,也就是这样,进而衍生出了下面这个算法的思想。通过只保留最后的估计 x ^ n − 1 , n − 1 \hat x_{n-1,n-1} x^n−1,n−1会更具实用性,并在每次测量后更新它,从而极大的减小了内存的需求也提升了算法的效率。
下图举例说明了所需的算法:
- 以时间点n举例,状态转移(或者成为预测矩阵)为1,
根据测量 z n z_n zn和先前的预测** x ^ n , n − 1 \hat x_{n,n-1} x^n,n−1=1* x ^ n − 1 , n − 1 \hat x_{n-1,n-1} x^n−1,n−1估计当前状态 x ^ n , n \hat x_{n,n} x^n,n - 使用动态模型根据当前状态 x ^ n , n \hat x_{n,n} x^n,n估计预测下一个状态** x ^ n + 1 , n \hat x_{n+1,n} x^n+1,n=1* x ^ n , n \hat x_{n,n} x^n,n

上面两个步骤,就是卡尔曼滤波的update和predict。
重点来了,根据上面的步骤我们能得到一个公式,也就是卡尔曼滤波的五个公式之一状态更新等式:
x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1)
上面公式里的因子 1 n \frac{1}{n} n1是特定于这个称金条的例子,而在卡尔曼滤波中,这个因子就是大名鼎鼎的卡尔曼增益,一般用 K n K_n Kn表示,下角标n表示每次迭代改值会随着更新。所以卡尔曼滤波算法的状态更新等式如下图:
x ^ n , n = x ^ n , n − 1 + K n ( z n − x ^ n , n − 1 ) \hat x_{n,n}=\hat x_{n,n-1}+K_n(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+Kn(zn−x^n,n−1)
x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1)这个公式详细的推导过程如下:
x ^ n , n = 1 n ∑ i = 1 n z i 测量 n 次后求均值 = 1 n ( ∑ i = 1 n − 1 z i + z n ) 将 z n 从求和式中提出 = 1 n ∑ i = 1 n − 1 z i + 1 n z n z n 单独提出来 = n − 1 n 1 n − 1 ∑ i = 1 n − 1 z i + 1 n z n 给第一项配相应的参数,从而进行代换 = n − 1 n x ^ n − 1 , n − 1 + 1 n z n 因为根据定义 x ^ n − 1 , n − 1 = 1 n − 1 ∑ i = 1 n − 1 z i = x ^ n − 1 , n − 1 − 1 n x ^ n − 1 , n − 1 + 1 n z n 拆分第一项 = x ^ n − 1 , n − 1 + 1 n ( z n − x ^ n − 1 , n − 1 ) 移项合并 \begin{split} \hat x_{n,n}&=\frac{1}{n}\sum_{i=1}^n{z_i}\space\space\space\space测量n次后求均值\\ &=\frac{1}{n}(\sum_{i=1}^{n-1}{z_i}+z_n)\space\space\space\space 将z_n从求和式中提出\\ &=\frac{1}{n}\sum_{i=1}^{n-1}{z_i}+\frac{1}{n}z_n\space\space\space\space z_n单独提出来\\ &=\frac{n-1}{n}\frac{1}{n-1}\sum_{i=1}^{n-1}{z_i}+\frac{1}{n}z_n\space\space\space\space 给第一项配相应的参数,从而进行代换\\ &=\frac{n-1}{n}\hat x_{n-1,n-1}+\frac{1}{n}z_n\space\space\space\space 因为根据定义\hat x_{n-1,n-1}=\frac{1}{n-1}\sum_{i=1}^{n-1}{z_i}\\ &=\hat x_{n-1,n-1}-\frac{1}{n}\hat x_{n-1,n-1}+\frac{1}{n}z_n\space\space\space\space 拆分第一项\\ &=\hat x_{n-1,n-1}+\frac{1}{n}(z_n-\hat x_{n-1,n-1})\space\space\space\space 移项合并 \end{split} x^n,n=n1i=1∑nzi 测量n次后求均值=n1(i=1∑n−1zi+zn) 将zn从求和式中提出=n1i=1∑n−1zi+n1zn zn单独提出来=nn−1n−11i=1∑n−1zi+n1zn 给第一项配相应的参数,从而进行代换=nn−1x^n−1,n−1+n1zn 因为根据定义x^n−1,n−1=n−11i=1∑n−1zi=x^n−1,n−1−n1x^n−1,n−1+n1zn 拆分第一项=x^n−1,n−1+n1(zn−x^n−1,n−1) 移项合并
称金条中蕴含的卡尔曼滤波的思想(必看)
看完上面称金条的例子,大家可能觉得多称几次,取平均这样的操作不是基本操作吗?至于底层理论大家都知道是为了减少测量过程中的随机误差,从而获取到更准确的期望值。
但是其实这个跟卡尔曼滤波的思想是一致的,也就是通过不停的称重(卡尔曼滤波中称为迭代),降低随机误差带来的影响,在不确定性中获取到最优的那个估计量。
x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) x ^ n , n = x ^ n , n − 1 + K n ( z n − x ^ n , n − 1 ) \begin{align} \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1})\\ \hat x_{n,n}=\hat x_{n,n-1}+K_n(z_n-\hat x_{n,n-1})\end{align} x^n,n=x^n,n−1+n1(zn−x^n,n−1)x^n,n=x^n,n−1+Kn(zn−x^n,n−1)
上面(1)式是求金条重量的公式,(2)式是卡尔曼滤波的状态更新公式,五大重要公式之一的状态更新公式。
下面重点来了,只要看完了下面的推导过程,你就会理解卡尔曼滤波的思想了,建立起卡尔曼滤波的直觉
根据上面(1)式和(2)式,求金条重量的例子中,公式的卡尔曼增益 K n K_n Kn就等于 1 n \frac{1}{n} n1,其中n表示第n个时间点或者第n次称量金条重量。
那么为什么这里的卡尔曼增益会等于 1 n \frac{1}{n} n1呢?
反正我觉得不是一拍脑袋决定的,下面我从头推导一遍给大家看,也许会让你对多次测量求期望的场景有一个全新的认识,帮助大家在建模的时候能够更深入的去思考。
推导过程:
- 首先大家从直觉的角度出发,当你不知道一个东西的重量的时候,对它的性质也不了解,纯靠蒙的时候,无论你猜什么值,这个值的不确定性是非常大的,因为你是纯靠蒙的,所以它的初始不确定性可以定义为 P 0 , 0 = ∞ P_{0,0}=\infin P0,0=∞,这里不一定要是无穷大,你可以理解成是一个大数;然后它的初始评估重量为 x ^ 0 , 0 \hat x_{0,0} x^0,0,至于具体等于多少都无所谓,后面你将看到实际上它对结果基本没影响。
- 因为瞎猜的结果是不合适的,所以我们需要用工具来称量金条的重量,从而来降低瞎猜结果带来的不确定性,前面这句话很重要,因为卡尔曼滤波就是围绕着降低不确定性来获得最优的估计结果。那么请注意这里我们给的一个条件就是一个具有随机噪声误差的电子秤来称金条,而我们见的最多的随机噪声的分布就是服从均值为0,方差1的高斯分布;也就是称量出来的结果的不确定性就是噪声的方差1;还有一点就是由于这是一个静态的系统,所以我们可以认为电子秤的状态每次都等价,也就是它的噪声的方差可以认为是 R n = 1 R_n=1 Rn=1,n是称金条的序号。
- 根据前面两点,我们会得到初始评估不确定性 P 0 , 0 = ∞ P_{0,0}=\infin P0,0=∞,初始评估重量 x ^ 0 , 0 \hat x_{0,0} x^0,0,第一次称量金条的重量 z 1 z_1 z1,称重误差(不确定性) R n = 1 R_n=1 Rn=1
算法估计流程图
下图是直接用了原作者博客里面的图,画图我不太擅长,这里就直接套用了,大家将就看一下。

初始化(第0次迭代 initialize)
在没有其他条件的时候,大胆对初始重量 x ^ 0 , 0 \hat x_{0,0} x^0,0进行估计,从后面的推导结果来看,它对后续的影响不大,在咱们这个例子里没影响。由于不存在合理的先验知识的情况下,这个初始状态(重量)的不确定性(方差) p 0 , 0 = ∞ p_{0,0}= \infin p0,0=∞。
x ^ 0 , 0 = 1000 g p 0 , 0 = ∞ \hat x_{0,0}=1000g\\ p_{0,0}= \infin x^0,0=1000gp0,0=∞
预测(predict)
预测步骤是根据动态模型来进行的,也就是经过状态转移矩阵进行下一个时间点状态预测,根据我们前面的假定动态模型是静态的,不变的,所以预测过后的不确定性也和前面的一致,状态转移矩阵在这个例子里就是F=1,所以
F = 1 x ^ 1 , 0 = F ∗ x ^ 0 , 0 = 1000 g p 1 , 0 = p 0 , 0 = ∞ F=1\\ \hat x_{1,0}= F*\hat x_{0,0}=1000g\\ p_{1,0}=p_{0,0}= \infin F=1x^1,0=F∗x^0,0=1000gp1,0=p0,0=∞
第1次迭代
测量步骤(measure)
用秤第一次称量金条的重量,并且我们假定这个秤存在随机误差,不确定性为R=1,得到 z 1 = 1030 g R 1 = 1 z_1 = 1030g\\ R_1=1 z1=1030gR1=1
评估步骤(update)
首先直接套用前面的公式 x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1),因为第1轮次,n=1,公式更新为 x ^ 1 , 1 = x ^ 1 , 0 + 1 1 ( z 1 − x ^ 1 , 0 ) x ^ 1 , 1 = 1000 g + 1 ∗ ( 1030 g − 1000 g ) x ^ 1 , 1 = 1030 g \hat x_{1,1}=\hat x_{1,0}+\frac{1}{1}(z_1-\hat x_{1,0})\\ \hat x_{1,1}=1000g+1*(1030g-1000g)\\ \hat x_{1,1}=1030g x^1,1=x^1,0+11(z1−x^1,0)x^1,1=1000g+1∗(1030g−1000g)x^1,1=1030g
根据公式组 x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) x ^ n , n = x ^ n , n − 1 + K n ( z n − x ^ n , n − 1 ) \ \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1})\\ \hat x_{n,n}=\hat x_{n,n-1}+K_n(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1)x^n,n=x^n,n−1+Kn(zn−x^n,n−1)
我们知道该步骤的卡尔曼增益 K 1 = 1 1 = 1 K_1=\frac{1}{1}=1 K1=11=1,下面我们从卡尔曼滤波的思想来推导一下为什么 K 1 = 1 1 = 1 K_1=\frac{1}{1}=1 K1=11=1?
首先得到两个公式,一个是根据预测结果和测量结果对下一个时间点的评估的结果。那么我们可以想一下,我们需要从预测的结果获取多少比例的信息,从测量中获取多少信息才能得到最优的评估结果,所以我们假设从测量结果 z 1 z_1 z1中获取到 w 1 w_1 w1的信息,其中 0 < = w 1 < = 1 0<=w_1<=1 0<=w1<=1;那么我们从预测结果 x ^ 1 , 0 \hat x_{1,0} x^1,0获取 1 − w 1 1-w_1 1−w1的信息,。得到下面的公式: x ^ 1 , 1 = ( 1 − w 1 ) ∗ x ^ 1 , 0 + w 1 ∗ z 1 \hat x_{1,1}=(1-w_1)*\hat x_{1,0}+w_1*z_1 x^1,1=(1−w1)∗x^1,0+w1∗z1
那么再想一下, w 1 w_1 w1取什么值合适呢?光凭上面的公式是无法确认 w 1 w_1 w1的值。这个时候我们前面一直说的不确定性(方差)就派上用场了。
说到方差先补充一个知识,这样大家就比较好理解接下来的推导了。也就是 v a r ( a x ) = a 2 v a r ( x ) var(ax)=a^2var(x) var(ax)=a2var(x),这个公式自己手动去推导也不难得到,就是随机变量同乘一个常数a之后,它的方差将变为原来的 a 2 倍 a^2倍 a2倍。
根据 x ^ 1 , 0 \hat x_{1,0} x^1,0具有的不确定性(方差)为 p 1 , 0 p_{1,0} p1,0, z 1 z_1 z1具有的不确定性为 R 1 R_1 R1。根据上面的公式,那么我们将得到评估结果的不确定性了
p 1 , 1 = ( 1 − w 1 ) 2 ∗ p 1 , 0 + w 1 2 ∗ R 1 p_{1,1}=(1-w_1)^2*p_{1,0}+w_1^2*R_1 p1,1=(1−w1)2∗p1,0+w12∗R1
PS.1.至于为什么要将权重平方,就是方差的性质。
2.为什么评估结果的不确定性,是两个不确定性相加,我们默认的是评估误差和测量误差都服从高斯分布,可以通过两个高斯分布概率密度相乘得到相同的推导结果,也就是上面公式等驾驭两个高斯分布函数相乘之后得到的新的高斯分布。
关键步骤:
那么我们认为经过预测结果和测量结果结合之后,不确定性变得最小,得到的结果就是最优的评估结果,这个思想就是卡尔曼滤波的核心思想。
那么要求 p 1 , 1 p_{1,1} p1,1最小,我们可以对上面公式右边求导数,对 w 1 w_{1} w1的导数。推导如下:
p 1 , 1 = ( 1 − w 1 ) 2 ∗ p 1 , 0 + w 1 2 ∗ R 1 求导 ∂ p 1 , 1 ∂ w 1 = 2 w 1 ∗ R 1 − 2 ∗ ( 1 − w 1 ) p 1 , 0 ∂ p 1 , 1 ∂ w 1 = w 1 ∗ R 1 − ( 1 − w 1 ) p 1 , 0 \begin{split} p_{1,1}&=(1-w_1)^2*p_{1,0}+w_1^2*R_1\space\space 求导\\ \frac{\partial p_{1,1}}{\partial w_1}&=2w_1*R_1-2*(1-w_1)p_{1,0}\\ \frac{\partial p_{1,1}}{\partial w_1}&=w_1*R_1-(1-w_1)p_{1,0}\\ \end{split} p1,1∂w1∂p1,1∂w1∂p1,1=(1−w1)2∗p1,0+w12∗R1 求导=2w1∗R1−2∗(1−w1)p1,0=w1∗R1−(1−w1)p1,0
上面右边是一个关于 w 1 w_1 w1的一元二次函数,当导函数等于0的时候, p 1 , 1 p_{1,1} p1,1取得极小值(高中的数学知识了,大家应该都知道的)所以得到下面:
∂ p 1 , 1 ∂ w 1 = w 1 ∗ R 1 − ( 1 − w 1 ) p 1 , 0 = 0 0 = w 1 ∗ R 1 − ( 1 − w 1 ) p 1 , 0 w 1 = p 1 , 0 R 1 + p 1 , 0 \begin{split} \frac{\partial p_{1,1}}{\partial w_1}&=w_1*R_1-(1-w_1)p_{1,0}=0\\ 0&=w_1*R_1-(1-w_1)p_{1,0}\\ w_1&=\frac{p_{1,0}}{R_1+p_{1,0}} \end{split} ∂w1∂p1,10w1=w1∗R1−(1−w1)p1,0=0=w1∗R1−(1−w1)p1,0=R1+p1,0p1,0
所以
K 1 = p 1 , 0 R 1 + p 1 , 0 K_1=\frac{p_{1,0}}{R_1+p_{1,0}} K1=R1+p1,0p1,0
将 p 1 , 0 = ∞ p_{1,0}=\infin p1,0=∞和 R 1 = 1 R_1=1 R1=1代入到上面的公式,得到 w 1 ≈ 1 w_1 \approx 1 w1≈1
而从公式来看卡尔曼增益 K 1 = w 1 = 1 K_1=w_1=1 K1=w1=1,所以从卡尔曼滤波角度来推导, K 1 = w 1 = 1 1 K_1=w_1=\frac{1}{1} K1=w1=11.
好了最重要的推导过程已经结束了,在这里大家应该都理解了什么是卡尔曼增益了吧,对卡尔曼滤波有了一个比较清晰的认识,建立起了对卡尔曼滤波的直觉。接下来就是循环上述步骤。
评估不确定性等于
p 1 , 1 = ( 1 − w 1 ) 2 ∗ p 1 , 0 + w 1 2 ∗ R 1 p_{1,1}=(1-w_1)^2*p_{1,0}+w_1^2*R_1 p1,1=(1−w1)2∗p1,0+w12∗R1将 w 1 = 1 w_1=1 w1=1和 R 1 = 1 R_1=1 R1=1代入到式子中去,得到 p 1 , 1 = 1 p_{1,1}=1 p1,1=1;
x ^ 1 , 1 = ( 1 − w 1 ) ∗ x ^ 1 , 0 + w 1 ∗ z 1 x ^ 1 , 1 = 1 ∗ z 1 = 1030 g \hat x_{1,1}=(1-w_1)*\hat x_{1,0}+w_1*z_1\\ \hat x_{1,1} =1*z_1=1030g x^1,1=(1−w1)∗x^1,0+w1∗z1x^1,1=1∗z1=1030g
可以看到初始的估计重量,被忽略了,由于它的高不确定性
预测步骤
预测步骤是根据动态模型来进行的,也就是经过状态转移矩阵进行下一个时间点状态预测,根据我们前面的假定动态模型是静态的,不变的,所以预测过后的不确定性也和前面的一致,状态转移矩阵在这个例子里就是F=1,所以
F = 1 x ^ 2 , 1 = F ∗ x ^ 1 , 1 = 1030 g p 2 , 1 = 1 ∗ p 1 , 1 = 1 F=1\\ \hat x_{2,1}= F*\hat x_{1,1}=1030g\\ p_{2,1}=1*p_{1,1}= 1 F=1x^2,1=F∗x^1,1=1030gp2,1=1∗p1,1=1
到这里第一轮迭代就结束了,接下来同样方式推导。
第2次迭代
测量步骤(measure)
用秤第二次称量金条的重量,并且我们假定这个秤误差不变,存在随机误差,不确定性为R=1,得到 z 2 = 989 g R 2 = 1 z_2 = 989g\\ R_2=1 z2=989gR2=1
评估步骤(update)
首先直接套用前面的公式 x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1),因为第2轮次,n=2,
根据公式组 x ^ n , n = x ^ n , n − 1 + 1 n ( z n − x ^ n , n − 1 ) x ^ n , n = x ^ n , n − 1 + K n ( z n − x ^ n , n − 1 ) \ \hat x_{n,n}=\hat x_{n,n-1}+\frac{1}{n}(z_n-\hat x_{n,n-1})\\ \hat x_{n,n}=\hat x_{n,n-1}+K_n(z_n-\hat x_{n,n-1}) x^n,n=x^n,n−1+n1(zn−x^n,n−1)x^n,n=x^n,n−1+Kn(zn−x^n,n−1)
我们知道该步骤的卡尔曼增益$K_2=\frac{1}{2},推导步骤在上面的第1轮迭代中。
K 2 = p 2 , 1 R 2 + p 2 , 1 = 1 1 + 1 = 1 2 K_2=\frac{p_{2,1}}{R_2+p_{2,1}}=\frac{1}{1+1}=\frac{1}{2} K2=R2+p2,1p2,1=1+11=21
公式更新为 x ^ 2 , 2 = x ^ 2 , 1 + 1 2 ( z 2 − x ^ 2 , 1 ) x ^ 2 , 2 = 1030 g + 1 2 ∗ ( 989 g − 1030 g ) x ^ 2 , 2 = 1009.5 g \hat x_{2,2}=\hat x_{2,1}+\frac{1}{2}(z_2-\hat x_{2,1})\\ \hat x_{2,2}=1030g+\frac{1}{2}*(989g-1030g)\\ \hat x_{2,2}=1009.5g x^2,2=x^2,1+21(z2−x^2,1)x^2,2=1030g+21∗(989g−1030g)x^2,2=1009.5g
p 2 , 2 = ( 1 − K 2 ) 2 ∗ p 2 , 1 + K 2 2 ∗ R 2 = 1 2 p_{2,2}=(1-K_2)^2*p_{2,1}+K_2^2*R_2=\frac{1}{2} p2,2=(1−K2)2∗p2,1+K22∗R2=21
预测步骤
预测步骤是根据动态模型来进行的,也就是经过状态转移矩阵进行下一个时间点状态预测,根据我们前面的假定动态模型是静态的,不变的,所以预测过后的不确定性也和前面的一致,状态转移矩阵在这个例子里就是F=1,所以
F = 1 x ^ 3 , 2 = F ∗ x ^ 2 , 2 = 1009.5 g p 3 , 2 = 1 ∗ p 2 , 2 = 1 2 F=1\\ \hat x_{3,2}= F*\hat x_{2,2}=1009.5g\\ p_{3,2}=1*p_{2,2}= \frac{1}{2} F=1x^3,2=F∗x^2,2=1009.5gp3,2=1∗p2,2=21
后面步骤我就省略一点
第3个迭代
z 3 = 1017 g R 3 = 1 z_3 = 1017g\\ R_3=1 z3=1017gR3=1
K 3 = p 3 , 2 R 3 + p 3 , 2 = 1 / 2 1 + 1 / 2 = 1 3 K_3=\frac{p_{3,2}}{R_3+p_{3,2}}=\frac{1/2}{1+1/2}=\frac{1}{3} K3=R3+p3,2p3,2=1+1/21/2=31
x ^ 3 , 3 = x ^ 3 , 2 + K 3 ( z 3 − x ^ 3 , 2 ) x ^ 3 , 3 = 1009.5 g + 1 3 ∗ ( 1017 g − 1009.5 g ) x ^ 3 , 3 = 1012 g \hat x_{3,3}=\hat x_{3,2}+K_3(z_3-\hat x_{3,2})\\ \hat x_{3,3}=1009.5g+\frac{1}{3}*(1017g-1009.5g)\\ \hat x_{3,3}=1012g x^3,3=x^3,2+K3(z3−x^3,2)x^3,3=1009.5g+31∗(1017g−1009.5g)x^3,3=1012g
p 3 , 3 = ( 1 − K 3 ) 2 ∗ p 3 , 2 + K 3 2 ∗ R 3 = 1 3 p_{3,3}=(1-K_3)^2*p_{3,2}+K_3^2*R_3=\frac{1}{3} p3,3=(1−K3)2∗p3,2+K32∗R3=31
F = 1 x ^ 4 , 3 = F ∗ x ^ 3 , 3 = 1012 g p 4 , 3 = 1 ∗ p 3 , 3 = 1 3 F=1\\ \hat x_{4,3}= F*\hat x_{3,3}=1012g\\ p_{4,3}=1*p_{3,3}= \frac{1}{3} F=1x^4,3=F∗x^3,3=1012gp4,3=1∗p3,3=31
第4个迭代
z 4 = 1009 g R 4 = 1 z_4= 1009g\\ R_4=1 z4=1009gR4=1
K 4 = p 4 , 3 R 4 + p 4 , 3 = 1 / 3 1 + 1 / 3 = 1 4 K_4=\frac{p_{4,3}}{R_4+p_{4,3}}=\frac{1/3}{1+1/3}=\frac{1}{4} K4=R4+p4,3p4,3=1+1/31/3=41
x ^ 4 , 4 = x ^ 4 , 3 + K 4 ( z 4 − x ^ 4 , 3 ) x ^ 4 , 4 = 1012 g + 1 4 ∗ ( 1009 g − 1012 g ) x ^ 4 , 4 = 1011.25 g \hat x_{4,4}=\hat x_{4,3}+K_4(z_4-\hat x_{4,3})\\ \hat x_{4,4}=1012g+\frac{1}{4}*(1009g-1012g)\\ \hat x_{4,4}=1011.25g x^4,4=x^4,3+K4(z4−x^4,3)x^4,4=1012g+41∗(1009g−1012g)x^4,4=1011.25g
p 4 , 4 = ( 1 − K 4 ) 2 ∗ p 4 , 3 + K 4 2 ∗ R 4 = 1 4 p_{4,4}=(1-K_4)^2*p_{4,3}+K_4^2*R_4=\frac{1}{4} p4,4=(1−K4)2∗p4,3+K42∗R4=41
F = 1 x ^ 5 , 4 = F ∗ x ^ 4 , 4 = 1011.25 g p 5 , 4 = 1 ∗ p 4 , 4 = 1 4 F=1\\ \hat x_{5,4}= F*\hat x_{4,4}=1011.25g\\ p_{5,4}=1*p_{4,4}= \frac{1}{4} F=1x^5,4=F∗x^4,4=1011.25gp5,4=1∗p4,4=41
第5个迭代
z 5 = 1013 g R 5 = 1 z_5= 1013g\\ R_5=1 z5=1013gR5=1
K 5 = p 5 , 4 R 5 + p 5 , 4 = 1 / 4 1 + 1 / 4 = 1 5 K_5=\frac{p_{5,4}}{R_5+p_{5,4}}=\frac{1/4}{1+1/4}=\frac{1}{5} K5=R5+p5,4p5,4=1+1/41/4=51
x ^ 5 , 5 = x ^ 5 , 4 + K 5 ( z 5 − x ^ 5 , 4 ) x ^ 5 , 5 = 1011.25 g + 1 5 ∗ ( 1013 g − 1011.25 g ) x ^ 5 , 5 = 1011.6 g \hat x_{5,5}=\hat x_{5,4}+K_5(z_5-\hat x_{5,4})\\ \hat x_{5,5}=1011.25g+\frac{1}{5}*(1013g-1011.25g)\\ \hat x_{5,5}=1011.6g x^5,5=x^5,4+K5(z5−x^5,4)x^5,5=1011.25g+51∗(1013g−1011.25g)x^5,5=1011.6g
p 5 , 5 = ( 1 − K 5 ) 2 ∗ p 5 , 4 + K 5 2 ∗ R 5 = 1 5 p_{5,5}=(1-K_5)^2*p_{5,4}+K_5^2*R_5=\frac{1}{5} p5,5=(1−K5)2∗p5,4+K52∗R5=51
F = 1 x ^ 6 , 5 = F ∗ x ^ 5 , 5 = 1011.6 g p 6 , 5 = 1 ∗ p 5 , 5 = 1 5 F=1\\ \hat x_{6,5}= F*\hat x_{5,5}=1011.6g\\ p_{6,5}=1*p_{5,5}= \frac{1}{5} F=1x^6,5=F∗x^5,5=1011.6gp6,5=1∗p5,5=51
后面五个迭代我就不写了,我直接把结果给出来,反正就是按照上面一样的步骤就可以。
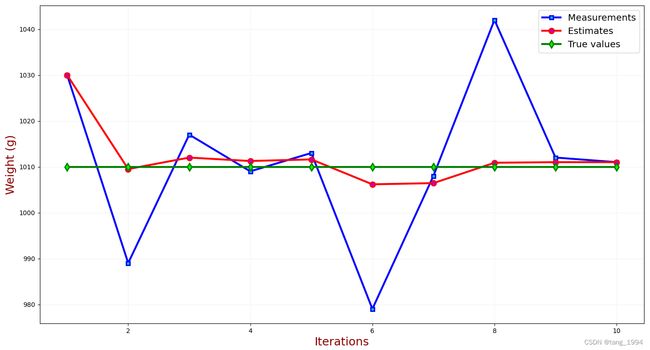
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| K n K_n Kn | 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | 1/10 |
| z n z_n zn | 1030 | 989 | 1017 | 1009 | 1013 | 979 | 1008 | 1042 | 1012 | 1011 |
| x ^ n , n \hat x_{n,n} x^n,n | 1030 | 1009.5 | 1012 | 1011.25 | 1011.6 | 1006.17 | 1006.43 | 1010.87 | 1011 | 1011 |
| x ^ n + 1 , n \hat x_{n+1,n} x^n+1,n | 1030 | 1009.5 | 1012 | 1011.25 | 1011.6 | 1006.17 | 1006.43 | 1010.87 | 1011 | 1011 |
从上面的图表中,可以看出,最终金条的重量是向着真实重量收敛的。
参考文档