OM | OR青年——可替换组件多阶段供应保障模型和动态协调机制研究

作者：朱晨希 浙江大学管理科学与工程专业在读硕士生

编者按：
可替换组件（LRU）的库存管理是一个非常重要的问题，它影响后勤支持过程中的系统可用性和运营成本。本文通过马尔可夫方法模拟库存变化的过程，为决策者的库存管理提供数据支持。

一、背景

为了保持高水平的系统可用性，可替换组件（LRU）被广泛地部署在资本密集型系统上。LRU 是一种按照通用规格设计的机电一体化组件的黑盒子，可以在一级维修设施中快速更换；例如，空客和波音商用飞机上的航空运输无线电和模块化组件单元。

可以更换的性质使得备用 LRU 的库存管理成为一个非常重要的问题，它影响后勤支持过程中的系统可用性和运营成本。一般来说，系统的可用性需要改进，同时减少由备用单元产生的库存成本。LRU 在货架上停留的时间越长，库存成本就越高，它由于技术变化而过时的风险也就越高。例如，在 1997 年，商业航空工业拥有价值超过 520 亿美元的备件库存，约 45%是可修复的备件。事实上，飞机的备件成本通常远远超过飞机本身的成本。

在本文中，我们主要关注一个如图 1 所示的集中控制的库存系统。例如，英国皇家空军在这样一个系统下运行，大约有 855000 个线路可更换项目。当零件失效时，将从库存中拆卸替换全新的 LRU，将系统恢复到服务。出现故障的 LRU 将在维修中心进行修复，并作为完全可用的备用单元重新进入库存。

二、模型描述

2.1 模型假设

我们假设系统由N个同种类型的零件组成，这些零件共享一个备用仓库。虽然这些组件是相同的，但它们可能包含在不同的子系统中，可能在不同的条件下运行，可能导致不同的故障率。如果更换了一个组件，则会丢弃旧组件，并且新组件处于最新状态0。由于与部件的预期寿命（年）和备件的交货时间（月）相比，维修时间通常较小（天），因此假设更换是即时的、替换零件不需要时间，但只能在有所需备件时才计划更换。备件可以订购任何数量，并在1个周期的固定交货时间（通常以月为顺序）后到达。如果某个零件出现很严重的故障以至于不能使用，修复故障件需要的时间为1个周期。同时我们假设库存订购策略为（s,S）。

2.2 事件发生顺序

事件发生的顺序如下。在每个时间单位开始时，可以到达上一期下单的备件订单（只要上一期下了订单）。接下来，对每个组件产生所谓的运营成本，这取决于组件的状态。设$O^j$表示运营成本。如果组件 j 处于状态 u，则每个时间单位的运行成本为$O_u^j$ 。这样，不仅可以包括故障组件的停机成本，而且还可以包括由于组件恶化而造成的收入损失的成本。在产生运营成本后，只要手头有足够的备件，就可以更换部件。在产生运营成本后，只要手头有足够的备件，就可以更换部件。在实践中，纠正性更换有时比预防性更换更昂贵，因为一个部件故障也会对系统的其他部件造成损坏。更换零件 j 的成本为$R^j$。在执行可能的维护操作后，可以订购备件，每订单产生固定成本 F。此成本与所订购的备件的数量无关。对于在时间单位结束时仍有的每个备件，将产生持有成本 H。

2.3 参数设定

三、马尔可夫决策过程

3.1 状态空间

设备状态诊断基于状态维护策略而提出，其认为设备是存在一个性能退化过程的，退化过程中设备的性能及故障率都会随之发生变化，而不是绝对的非健康则故障。举例来说，轴承磨损程度决定其性能，所以通常采用无磨损、轻微磨损、正常磨损、严重磨损等分类方式代表其运行状态。

本文将零件性能退化过程中的运行状态统一划分为健康、良好、正常、劣化和故障 5个等级。

我们可以首先对状态监测系统的数据进行采集、抽样，然后将所有参数数据归一化，生成一组[0,1]之间的无量纲数值，数值越小代表设备运行状态越好，最后通过在[0,1]之间划定不同的数值界限，对应不同的零件状态等级。所以只要我们能够通过监测系统采集不同零件的主要性能参数数据，并获得相应的数据处理结果，就可以基于上述状态分级方法，得到相应的状态等级划分结果。

3.2 动作空间

3.3 状态转移

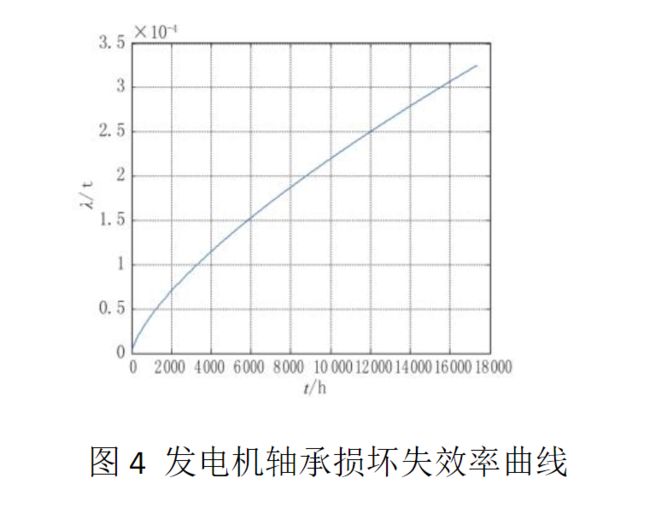
在实际应用中，可以通过失效率曲线估算状态转移的概率。以风电机组运行过程中发电机部分的2个故障模式发电机碳刷磨损、发电机轴承的失效率为例：

发电机碳刷磨损故障表现为早期故障模式，设备投运初期故障率较高，运行一段时间后，故障率趋于平稳并不会随着时间而变大。

发电机轴承损坏的失效率曲线呈现明显的损耗故障特征，主要故障原因是轴承的疲劳损伤。

3.4 预期成本

3.5 （s,S）库存策略

四、学习心得

我选择的细分课题是基于信息松弛方法的维修备件库存管理。八周跟随孙老师的学习干货满满。在第一周，我了解了 LRU 相关问题所处的背景资料，了解到可修复备件在备件供应保障结构中是循环库存模式，在实际中可修复备件一般价格昂贵、占用库存资金比重大，可以经多次修复使用。在军用航空场景下应用较多，航空备件保障直接影响飞机的快速出动和高强度出动。

在第二周，我学习了David Brown 在operations research 发表的文章，了解到可以用启发式策略以确定最优库存水平的下界，使用信息松弛（Information Relaxation）的方法解决POMDP 问题，找到松弛问题和原始问题之间的联系，并构造函数来惩罚来自额外信息的收益，以此来估计库存水平最优值的上界和下界；

在第三周，我跟随着David Brown 文章进行了数学推导，了解到动态规划的目标是选择一个策略以最大化预期的总回报，在动态规划中决策者的选择是未知的，因此在t 周期的行动选择只取决于t 周期开始时已知的内容。我们假设在时间段t 内的回报是可观测的并且只依赖于第一个t+1 动作，我们为每一个结果选择一个最优动作a。通过文献我还学习到了信息松弛分为三种，完美的信息松弛、较紧密的信息松弛、紧密的信息松弛。完美的信息松弛中，成本序列、需求分布和实际需求都是随机生成的，即假设成本、需求分布和实际需求都是已知的。而第二种信息松弛，它假设需求分布和实际需求是已知的，但订购成本是未知的，随机生成需求分布和需求。第三种最紧密的信息松弛是只假设需求分布是已知的，但是实际成本和实际需求是未知的。

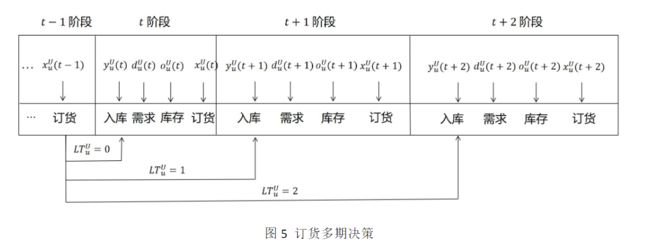
在第四周，我对LRU 问题的多期决策过程进行了梳理，此时我规定状态变量为库存水平，决策变量为订货量，如图5 所示。

在第五周，我在模型中考虑到了设备的状态，重新定义了决策变量为维护设备动作，即根据设备当前寿命$t_n$和状态$i$，从最优策略集合中挑选出最优维护动作。此时，孙老师指出我的问题确定的并不清楚，并让我重新考虑一下基本的换零件返修的库存订货模型。

在第六周，我考虑了一个基本的换零件返修的库存模型，并假设库存策略为缺货多少补货多少。我假设第一期故障零件有$a_1$个（$a_1$是随机变量），库存有$z_1$个（$z_1$为给定常量），如果$z_1\ge a_1$，那就选择在当期立即拆卸并替换$a_1$个零件，并且修复并存储其中1部分，并在第二期进行存储（假设修复零件需要一个周期）。如果$z1\le a_1$，那么需要订货$a_1-z_1$个，并修复并存储其中${\delta }_1$部分，如图6 所示。

在第七周，我将状态空间定义为系统是否有故障出现，动作空间定义为是否检测并替换故障零件。此时，孙老师及时发现了我的错误，发现我对于动态规划的基本知识并不了解，对我进行了指导并给了我一些参考资料，其中包括Sheldon Ross 写的动态规划书籍Introduction to stochastic dynamic programming 和孙老师POMDP 的讲座视频资料。

在第八周，我参考Minou 的文章对于模型进行了重新调整，在定义状态空间时同时考虑到了零件状态和库存水平。

参考文献

[1]Minou C. A. Olde Keizer & RuRuud H. Teunter etc.(2016). Joint condition-based maintenance and inventory optimization for systems with multiple components.European Journal of Operational Research,257:209-222.

[2] Alain Bensoussan, Pengfefei Guo. (2015).Technical Note—Managing Nonperishable Inventories with Learning About Demand Arrrrival Rate Through Stockout Times. OperationsResearch,63(3):602-609.

[3] David B. Brown & James E. Smith etc.(2010).Information relaxations and duality in stochastic dynamic programs.Operations Research, 58(4): 785–801.

[4] Xiao Liu & Loon Ching Tang (2016) Reliability analysis and spares provisioning for repairable systems with dependent failure processes and a time-varying installed base, IIE Transactions, 48:1, 43-56, DOI: 10.1080/0740817X.2015.1055391