CNN的Python实现——第六章:梯度反向传播算法
文章目录
- 第6章 梯度反向传播算法
-
- 6.1 基本函数的梯度
- 6.2 链式法则
- 6.3 深度网络的误差反向传播算法
- 6.4 矩阵化
- 6.5 softmax损失函数梯度计算
- 6.6 全连接层梯度反向传播
- 6.7 激活层梯度反向传播
- 6.8 卷积层梯度反向传播
- 6.9 最大值池化层梯度反向传播
第6章 梯度反向传播算法
本章的核心问题是: 给定参数化模型的损失函数 f ( x , w ) f(x,w) f(x,w),其中 x x x 是输入数据, w w w 是模型参数,需要计算损失函数关于参数 w w w 的梯度。有了梯度,我们就能使用梯度下降法的各种改进方法进行模型优化了。注意损失函数输出的是标量,是一个数值,而不是向量或矩阵。
6.1 基本函数的梯度
神经网络模型包含最基本的三种函数:乘法、加法和非线性激活Re LU。这三种函数的梯度计算都非常简单,列举如下:

这里所有的变量都是标量,为一个数值。 I ( x ) I(x) I(x) 是指示函数,当括号内的表达式为真时输出1 ,否则输出 0 。注意 m a x ( 0 , x ) max(0,x) max(0,x) 函数,在 0 点导数不连续,但是右导数为 1 ,左导数为 0 ,存在次导数。读者需要牢记偏导数的意义为函数值对于该变量的敏感程度,偏导数越大说明越敏感。偏导数为正, 表示变量增加,函数值增加,是正相关; 偏导数为负,表示变量增加,函数值减小,是负相关。
6.2 链式法则
对于复合函数,求梯度需采用链式法则。链式法则的内容如下:
z = f ( y ) , y = g ( x ) z=f(y),y=g(x) z=f(y),y=g(x)
则: ∂ z ∂ x = ∂ z ∂ y ∂ y ∂ x \frac{{\partial z}}{{\partial x}} = \frac{{\partial z}}{{\partial y}}\frac{{\partial y}}{{\partial x}} ∂x∂z=∂y∂z∂x∂y,即 z z z 对 变量 x x x 的梯度是 z z z 对中间变量 y y y 的梯度与 y y y 对变量 x x x 的梯度的乘积。
常规神经网络和卷积网络都是多层网络,多层网络从函数角度看,就是复合函数。举个例子,为了突出链式法则,我们对模型进行简化,忽略偏置,令神经网络的每层神经元数量都为I ,这样都是标量,简化了偏导数求解, 当两层的常规神经网络用于回归任务时, 其数学模型为:
a 1 = x w 1 , h 1 = max ( 0 , a 1 ) , a 2 = h 1 w 2 , l o s s = 1 2 ( a 2 − y 0 ) 2 {a_1} = x{w_1},\ {h_1} = \max (0,{a_1}),\ \ {a_2} = {h_1}{w_2}, \ \ loss = \frac{1}{2}{({a_2} - {y_0})^2} a1=xw1, h1=max(0,a1), a2=h1w2, loss=21(a2−y0)2
其中 x x x 是输入, y 0 y_0 y0 是 x x x 对应的标签, 即需拟合的真实值。为了求 loss 对参数 w 1 w_1 w1 的梯度,必须采用链式法则,先求每个函数的梯度,然后所有梯度连乘,得到最终梯度:
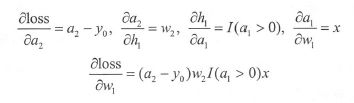
这个例子表明,利用链式法则求梯度,只要能求得每个中间函数的梯度,则最终的梯度就是每个梯度的乘积。中间函数就是每层的变换函数,它们都由三种基本函数组成,求解十分简单,所以不存在困难。
这是一个稍微复杂的例子,函数形式:
f = x + y 2 x + y f = \frac{{x + y}}{{2x + y}} f=2x+yx+y
求 f f f 对 x x x 的偏导数。读者可以采用高数的方法直接求偏导数,这里 为了清晰地展示链式法则和理解深度网络,我们采用分步法。分步法的关键是一个复杂函数通过中间变量,使之变成简单模块的嵌套,每个简单模块能直接利用公式得到偏导数,每个模块相当于一层网络。具体如下,先通过一些中间变量来计算函数值:
n u m = x + y , d e n = 2 x + y , i n v d e n = 1 / d e n , f = n u m × i n v d e n num=x+y, \ den=2x+y, \ invden = 1/den, \ f=num \times invden num=x+y, den=2x+y, invden=1/den, f=num×invden
再对每个函数求偏导数,得:

这里有两个路径可以得到 f f f 对 x x x 的偏导数:

一定要注意,最终结果是这两个偏导数之和。
6.3 深度网络的误差反向传播算法
本节采用 n n n 层网络模型,求损失函数对参数的偏导,达到深刻理解梯度反向传播规律的目的这对理解深度网络训练特别有帮助。
同理,本节为了突出梯度反向传播规律,简化数学处理,令深度神经网络的每层神经元数量都为1 ,这样都是标量,简化了求偏导数。神经网络用于回归任务,设 x x x 是输入, y 0 y_0 y0 是 x x x 对应的标签, 即需拟合的真实值, h n h_n hn 是网络的预测值, f ( x ) f(x) f(x) 是非线性激活函数。令 h 0 h_0 h0 等于 x x x , f ’ ( a n ) f’( a_n) f’(an) 等于 1 ,则数学模型为:
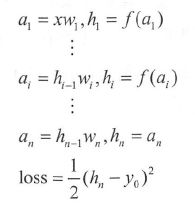
首先,对每层求偏导数, 然后进行连乘,就能得到损失 loss 对任一层 参数 w i w_i wi 的梯度:
∂ l o s s ∂ w i = ( h n − y 0 ) ∏ j = i + 1 n w j ∏ j = i n f ′ ( a j ) h i − 1 \frac{{\partial loss}}{{\partial {w_i}}} = ({h_n} - {y_0})\prod\limits_{j = i + 1}^n {{w_j}} \prod\limits_{j = i}^n {f'({a_j}){h_{i - 1}}} ∂wi∂loss=(hn−y0)j=i+1∏nwjj=i∏nf′(aj)hi−1
这里有几点请读者注意:
- h n − y 0 {h_n} - {y_0} hn−y0 是预测值和真实值之间的误差,乘积中的变量是从最后一层开始向前递推的,所以该方法称为误差反向传播算法。有误差,就有梯度,就能学习,直到误差为0 , 学习才结束。
- 表达式中有中间变量 a j a_j aj,所以为了加快梯度计算, 需要在网络的前向计算过程中存储中间变量, 但这样会占用大量内存。
- 表达式中含有权重的乘积,所以如果权重初始化得过小,梯度就会很小,导致学习速度慢。因为权重的绝对值小于1 ,所以相乘的项越多,乘积越小,这导致越是靠前的层( i i i 较小)的参数越难学习。
- 表达式中有非线性激活函数导数的乘积。当激活函数采用sigmoid 或tanh 等函数时,由于其导数绝对值均小于 1 ,且存在饱和(导数趋近0 ),这样乘积会很小。特别是对于网络前面的层,乘积会更小。这种现象在浅层网络不明显,但在深度网络中特别明显,因为层数 n 基本都在 10 以上,甚至成百上千。这样连乘的项很多,乘积会十分小( 0. 5 20 = 1 0 − 6 0.5^{20}= 10^{-6} 0.520=10−6 ),梯度太小会导致参数更新率低,学习困难。
- 如果激活函数是ReLU , ReLU 的导数为 I ( x > 0 ) I(x>0) I(x>0) ,即变量小于等于0 ,导数为0 ;变量大于0 ,导数为1 。当网络采用合适的参数进行初始化和数据归一化时,可假设网络各层中间变量 a j a_j aj 有一半的概率小于0 ,一半的概率大于0 ,这样 loss 对参数 w i w_i wi 的梯度为 0 的概率十分高并且随着 i i i 的减小会越来越高。当梯度为0 时,根据梯度下降法,参数将无法更新,不能进行学习。在深度卷积网络中,损失函数对前面几层参数的梯度包含大量激活函数梯度的连乘,只要有一层激活函数的梯度为 0,则整个表达式就为0 。因此,网络中大量参数的梯度会为0,易导致 “ ReLU 死亡 ” 问题,所以前面几层的参数很难进行有效学习。
- 如果激活函数是ReLU , 虽然大部分非线性激活函数导数的乘积是0 ,但还是有部分乘积不是0 ,则这些乘积就是1 (虽然所占比例不高),不会像sigmoid 函数那样,乘积都变得很小。乘积为 1 时,学习就比较容易,所以 ReLU 的收敛速度比 sigmoid 快不少,这也是 ReLU 大量使用的原因。
6.4 矩阵化
实际的网络中,所有的变量(包括输入、中间变量和参数)都是矩阵,这样求中间函数的梯度就是求矩阵对矩阵的梯度,非常困难。在上面的例子中,由于变量都是标量,所以中间函数的梯度也是标量,十分简单。这里通过一个数学技巧,避免直接计算中间函数的梯度,达到简化计算的目的,而且更便于理解。
因为损失函数是标量,最终的目的是计算损失函数对参数的梯度,且标量对矩阵参数的梯度是矩阵,所以梯度矩阵的尺寸和矩阵参数的尺寸一致。利用这个性质,能极大地简化梯度计算。任何机器学习模型的损失函数值都是标量,这一定要牢记在心,所以直接求损失函数对各层参数的梯度会十分方便。
网络最后一层输出分值向量(向量是矩阵的特例) S S S 。假设我们得到损失函数 loss 对 S S S 的梯度,该梯度简记为 d S dS dS (注意之后的损失函数对参数的梯度都简记为 d W dW dW,省略重复的 d l o s s dloss dloss ),注意 d S dS dS 和 S S S 的尺寸相同。网络最后两层的模型如下:
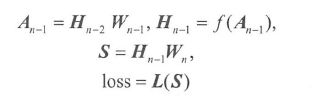
再次提醒此时所有变量都是矩阵,已经得到 d S dS dS 。现在从 d S dS dS 开始反向传播,推导其他变量的梯度。
- 首先,根据 S = H n − 1 W n S=H_{n-1}W_n S=Hn−1Wn 可以得到 H n − 1 H_{n-1} Hn−1, W n W_n Wn 的梯度,其值为: d H n − 1 = d S W n T dH_{n-1}=dSW_n^T dHn−1=dSWnT 和 d W n = H n − 1 T d S dW_n=H_{n-1}^TdS dWn=Hn−1TdS,其中矩阵上标 T T T表示矩阵的转置。
- 根据 H n − 1 = f ( A n − 1 ) H_{n-1} = f(A_{n-1}) Hn−1=f(An−1) 和 d H n − 1 dH_{n-1} dHn−1 可得 d A n − 1 = d H n − 1 f ′ ( A n − 1 ) dA_{n-1} = dH_{n-1}f'(A_{n-1}) dAn−1=dHn−1f′(An−1),注意该式是逐元素计算的,不是矩阵乘法。
- 有了 d A n − 1 dA_{n-1} dAn−1,再结合 A n − 1 = H n − 2 W n − 1 A_{n-1} = H_{n-2}W_{n-1} An−1=Hn−2Wn−1 可得: d H n − 2 = d A n − 1 W n − 1 T dH_{n-2} = dA_{n-1}W^T_{n-1} dHn−2=dAn−1Wn−1T 和 d W n − 2 = H n − 2 T d A n − 1 dW_{n-2} = H^T_{n-2}dA_{n-1} dWn−2=Hn−2TdAn−1
- 有了 d H n − 2 dH_{n-2} dHn−2,可以继续往前推,反向得到各层参数和中间变量的梯度,直到得到第一层参数的梯度和输入的梯度。
这里的核心是矩阵乘法 A = H W A=HW A=HW ,并且已知 d A dA dA ,求 d H dH dH 和 d W dW dW ,那么:

希望读者记住此公式,该公式比较好记【如果有兴趣,可以自己推一下】,首先把这些变量看成标量,则 d H = W d A , d W = H d A dH=WdA, \ \ dW=HdA dH=WdA, dW=HdA,然后把它们看作矩阵。由于矩阵乘法需要满足矩阵的尺寸一致性, 即尺寸为 m × n m \times n m×n 和尺寸为 n × k n × k n×k 的矩阵乘积为 m × k m × k m×k 的矩阵,两个相乘矩阵必须有个维度相等。可以发现,只有 d H = d A W T dH=dAW^T dH=dAWT 和 d W = H T d A d W=H^TdA dW=HTdA 的形式满足矩阵乘法的性质。
6.5 softmax损失函数梯度计算
softrnax 损失函数的定义:
p k = − log ( e s k / ∑ j = 1 K e s j ) L i = − log ( p y i ) \begin{array}{l} {p_k} = - \log \left( {{e^{{s_k}}}/\sum\limits_{j = 1}^K {{e^{{s_j}}}} } \right)\\ {L_i} = - \log ({p_{{y_i}}}) \end{array} pk=−log(esk/j=1∑Kesj)Li=−log(pyi)
其中 y i y_i yi 是样本 i i i 的标签,即样本类别的序号, p k p_k pk 是第 k k k 类的概率, s k s_k sk 是第 k k k 类的分值。现在求 ∂ L i / ∂ s k \partial {L_i}/\partial {s_k} ∂Li/∂sk ,利用高数知识,可以很容易求出该梯度:
∂ L i / ∂ s k = p k − I ( y i = k ) \partial {L_i}/\partial {s_k} = {p_k} - I({y_i} = k) ∂Li/∂sk=pk−I(yi=k)
其中, l ( y i = k ) l(y_i = k) l(yi=k) 表示当 k k k 等于标签 y i y_i yi 时,则结果等于 1 , 否则为 0 。这样
我们就得到了 d S dS dS,然后就可以进行6 .4 节的梯度反向传播,获得各层参数的梯度。
式( 6.14)十分简洁,同时具有启发意义
- 由于概率 p k p_k pk大于 0 ,所以当 k k k 不等于标签 y i y_i yi 时,梯度为: p k p_k pk 。
当梯度为正的时候,即: ∂ L i / ∂ s k > 0 \partial {L_i}/\partial {s_k}>0 ∂Li/∂sk>0
上式表示:随着分值 s k {s_k} sk 增加,损失值 L i {L_i} Li 也会增加;
这正是我们希望的:对于非类别对应的分值,希望其越小越好。 - 当 k k k 等于标签 y i y_i yi 时,梯度为: p y i − 1 < 0 p_{y_i}-1 <0 pyi−1<0 。
当梯度为正的时候,即: ∂ L i / ∂ s k < 0 \partial {L_i}/\partial {s_k}<0 ∂Li/∂sk<0
上式表示:随着分值 s k {s_k} sk 增加,损失值 L i {L_i} Li 会减小;
这正是我们希望的:对于样本的类别对应的分值,希望其越大越好。
(上述两点均是使得LOSS变小的分析)
实践中, 一般会对多个样本同时进行处理,代码如下:
import numpy as np
K = 10 # 类别数
N = 128 # 样本数量
scores = np.random.randn(N, K) # 一行一个样本的分值向量
labels = np.random.randint(K, size = N)
exp_scores = np.exp(scores)
exp_scores_sum = np.sum(exp_scores, axis = 1, keepdims=True)
probs = exp_scores/exp_scores_sum
dscores = probs.copy()
dscores[range(N), labels] -= 1 ## 语句1
dscores /= N
随机生成分值矩阵和样本标签,其中分值矩阵的一行是一个样本的分值向量。
然后计算概率矩阵和分值矩阵的梯度,最后取平均。
注意语句①的索引方式,用于获得样本的类别分值。
分值梯度dscores的尺寸和scores 一致, 每行对应一个样本。
6.6 全连接层梯度反向传播
全连接层梯度的计算和6.4 节所述很像,只是多了偏置。公式为

import numpy as np
D = 784 # 数据维度
K = 10 # 类别数
N = 128 # 样本数量
X = np.random.randn(N, D) # 一行一个样本
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
scores = np.dot(X, W) + b
# 反向传播
dscores = np.random.randn(N, K) # 与scores的尺寸一样
dX = np.dot(dscores, W.T)
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True) ## 1
首先前向计算分值矩阵,同样每一行是一个样本的分值向量。
随机生成分值矩阵的梯度dscores 后,计算 d X dX dX 和 d W dW dW。
需要特别注意语句①中 d b db db 的计算方式, d b db db 中的每个元素是 dscores 每列之和。因为如果不使用NumPy 的广播机制,则 b b b 向量需扩增为矩阵。计算 d b db db 的每个元素,有 N N N 条路径, N N N 条路径之和就是 d b db db 元素的值。
6.7 激活层梯度反向传播
首先,给出一个定义:对于 y = f ( x ) y=f(x) y=f(x) ,那么 d x = d y ⋅ f ′ ( x ) dx = dy \cdot f'(x) dx=dy⋅f′(x)
当激活函数采用ReLU 时,公式为 H o u t = R e L U ( H i n ) H_{out} = ReLU(H_{in}) Hout=ReLU(Hin), 其中 H i n H_{in} Hin 是激活层的输入, H o u t H_{out} Hout 是输出。注意,该公式是逐元素计算的。已知 d H o u t dH_{out} dHout,需要计算 d H i n dH_{in} dHin。 ReLU 的梯度计算特别简单,因为当输入小于0 时,梯度为0 ;当输入大于0 时,梯度为1 。所以 H i n H_{in} Hin 的每个元素只需简单地和 0 比较,如果大于0 , 则输出梯度等于输入梯度,否则为0。代码如下:
import numpy as np
dim1 = 164
dim2 = 128
Hin = np.random.randn(dim1, dim2)
Hout = np.maximum(0, Hin) # ReLU激活
dHout = np.random.randn(dim1, dim2) # 与Hout的尺寸一样
# 反向传播
dHin = dHout
dHin[Hin <= 0] = 0
对于随机生成的输入矩阵 H i n H_{in} Hin 和梯度 d H o u t dH_{out} dHout,先进行 ReLU 激活,输入梯度先赋值为输出梯度, 然后进行梯度反传,即把输入值 H i n H_{in} Hin 小于等于0 的梯度设置为0。该代码十分清晰地展示了梯度反向传播,但是增加了很多中间变量,存储开销比较大。实践中代码可以简化如下:
dim1 = 164
dim2 = 128
hidden_data = np.random.randn(dim1, dim2)
hidden_data = np.maximum(0, hidden_data) # ReLU激活
dhidden_data = np.random.randn(dim1, dim2) # 与hidden_data的尺寸一样
# 反向传播
dhidden_data[hidden_data <= 0] = 0 # ①
由于输入数据和输出数据的尺寸相同,又不需要存储中间结果,所以输入和输出数据可以共享存储空间,使用同一个变量。
与其他激活函数的梯度反向传播程序类似, 只是语句① 有所不同,现在以 ELU 激活函数为例进行介绍,公式为:

其梯度为:

而 e x = f ( x ) + 1 e^x = f(x)+1 ex=f(x)+1,所以语句①的代码为:dhidden_data[hidden_data<=0] *= (hidden_data+1)
6.8 卷积层梯度反向传播
卷积层的梯度反向传播比较复杂,本书采用大矩阵乘法来实现。梯度反向传播的计算过程和卷积层的正向计算过程正好相反,是其逆过程,所以本节首先简单回顾一下如何利用大矩阵乘法实现卷积层的正向计算过程。其核心有三步。
(1)将输入特征图变换为大矩阵 matric_data 。
(2)进行矩阵相乘和非线性激活( 等价于全连接层)后得到 filter_ data 。
(3)将filter_ data 变换为输出特征图。
卷积层梯度反向传播是己知输出特征图的梯度,求输入特征图的梯度及卷积核的梯度,其过程如下。
(1)把输出特征图的梯度 d o u t _ d a t a dout\_data dout_data 变换为矩阵形式(正向计算第( 3 ) 步的逆过程)。
(2)将全连接层和激活层的梯度进行反向传播。
(3)把第( 2 )步得到的大矩阵梯度变换为特征图形状的梯度,即得到输入特征图的梯度。
梯度反向传播时,需要正向计算过程得到的 matric_data 和 filter_data ,读者只要理解了正向计算过程,其逆过程很简单,所以这里直接给出代码。若需要示意图,可以参考4.2 . 5 节的图4.4 。
首先,定义一些超参数, 同时随机生成一些必要的数据,这些数据能够在正向计算中获得:
import numpy as np
filter_size = 3
filter_size2 = filter_size*filter_size
stride = 1
padding = (filter_size - 1)//2
batch = 8
(in_height, in_width, in_depth) = (32, 48, 16)
(out_height, out_width, out_depth) = (32, 48, 32)
out_size = out_height*out_width
dout_data = np.random.randn(batch, out_height, out_width, out_depth)
matric_data = np.random.randn( out_size*batch, filter_size2*in_depth )
filter_data = np.random.randn( out_size*batch, out_depth )
weights = 0.01 * np.random.randn(filter_size2*in_depth, out_depth)
其中, d o u t _ d a t a dout\_data dout_data 是上次梯度反向传播得到的,是输入梯度, m a t r i c _ d a t a matric\_data matric_data 、 f i l t e r _ d a t a filter\_data filter_data 和 w e i g h t s weights weights 都是在正向计算中得到的。
然后把 d o u t _ d a t a dout\_data dout_data 变换为矩阵形式 d f i l t e r _ d a t a dfilter\_data dfilter_data , 即尺寸与 f i l t e r _ d a t a filter\_data filter_data 一致。 d o u t _ d a t a dout\_data dout_data 的每个深度列就是 d f i l t e r _ d a t a dfilter\_data dfilter_data 的一行,代码如下:
#first backprop the dout_data to dfilter_data
#one depth of dout_data into one row of dfilter_data
dfilter_data = np.zeros_like(filter_data)
for i_batch in range(batch):
i_batch_size = i_batch*out_size
for i_height in range(out_height):
i_height_size = i_batch_size + i_height*out_width
for i_width in range(out_width):
dfilter_data[i_height_size + i_width, :] = dout_data[i_batch, i_height, i_width, :]
其次,进行激活层和全连接层反向传播,得到权重 d w e i g h t s dweights dweights 、偏置的梯度 d b i a s dbias dbias 以及矩阵形式的梯度 d m a t r i c d a t a dmatric_data dmatricdata:
#backprop the RELU non-linearity
dfilter_data[filter_data <= 0] = 0
#backprop the dot product filter_data = np.dot(matric_data, weights) + bias
dweights = np.dot(matric_data.T, dfilter_data)
dbias = np.sum(dfilter_data, axis=0, keepdims=True)
dmatric_data = np.dot(dfilter_data, weights.T)
最后, 把 d m a t r i c _ d a t a dmatric\_data dmatric_data 变换为特征图形状的梯度, 即得到输入特征图的梯度:
#backprop the dmatric_data to dpadding_data
padding_height = in_height + 2*padding
padding_width = in_width + 2*padding
dpadding_data = np.zeros((batch, padding_height, padding_width, in_depth) )
height_ef = padding_height - filter_size + 1
width_ef = padding_width - filter_size + 1
for i_batch in range(batch):
i_batch_size = i_batch*out_size
for i_h, i_height in zip(range(out_height), range(0, height_ef, stride)):
i_height_size = i_batch_size + i_h*out_width
for i_w, i_width in zip(range(out_width), range(0, width_ef, stride)):
dpadding_data[i_batch, i_height : i_height + filter_size,
i_width : i_width + filter_size, :] += dmatric_data[
i_height_size + i_w, :].reshape(filter_size, filter_size, -1) ## 语句①
#backprop the dpadding_data to din_data
if padding:
din_data = dpadding_data[:,padding:-padding,padding:-padding,:]
else:
din_data = dpadding_data
其中, d m a t r i c _ d a t a dmatric\_data dmatric_data 的每一行数据就是 d p a d d i n g _ d a t a dpadding\_data dpadding_data 的局部窗口的一个数据,注意行向量需要 reshape 成3D 矩阵。特别注意语句① 中的加号,这是因为 d p a d d i n g _ d a t a dpadding\_data dpadding_data 数据有多条路径(即局部窗口有重叠)得到梯度,所以需要累加。
现在有了 d i n _ d a t a din\_data din_data ,又可以向前一层进行梯度反向传播了,这样一层一层传播下去,直到第一层。
6.9 最大值池化层梯度反向传播
最大值池化层梯度反向传播类似于ReLU 激活层梯度反向传播。ReLU 是求 m a x ( 0 , x ) max(0, x) max(0,x) 的偏导数,最大值池化层是求 f = m a x ( a , b , c , d ) f= max(a,b, c, d) f=max(a,b,c,d) 的偏导数,其中 a , b , c a,b,c a,b,c 和 d d d 是输入 2 × 2 2 × 2 2×2 窗口的数据。该函数的偏导数很简单,对 a 、 b 、 c a、b 、c a、b、c 和 d d d 中最大值的梯度为1 ,其他为0 。计算过程如下。

import numpy as np
(batch, in_height, in_width, in_depth) = (8, 32, 48, 16)
filter_size = 2
filter_size2 = filter_size*filter_size
stride = 2
out_height = (in_height - filter_size)//stride + 1
out_width = (in_width - filter_size)//stride + 1
out_depth = in_depth
out_size = out_height*out_width
dout_data = np.random.randn(batch, out_height, out_width, out_depth)
matric_data_max_pos = np.random.randn(out_size*in_depth*batch, filter_size2) # 1
matric_data_max_pos = matric_data_max_pos > 0 # 2
matric_data_not_max_pos = ~matric_data_max_pos # 3
din_data = np.zeros((batch, in_height, in_width, in_depth), dtype = np.float64)
height_ef = in_height - filter_size + 1
width_ef = in_width - filter_size + 1
for i_batch in range(batch):
i_batch_size = i_batch*out_size*in_depth
for i_h_out, i_height in zip(range(out_height), range(0, height_ef, stride)):
i_height_size = i_batch_size + i_h_out*out_width*in_depth
for i_w_dout, i_w, i_width in zip(range(out_width),
range(0, in_depth*out_width, in_depth),
range(0, width_ef, stride)):
md = matric_data_not_max_pos[i_height_size + i_w : i_height_size + i_w + in_depth, : ] # 4
din = din_data[i_batch, i_height : i_height + filter_size,
i_width : i_width + filter_size, :] # 5
dout = dout_data[i_batch, i_h_out, i_w_dout, :] # 6
for i in range(filter_size):
for j in range(filter_size):
din[i, j, :] = dout[:] # 7
din[i, j, :][md[:, i*filter_size + j]] = 0 # 8


