机器学习实战 2.6选择和训练模型 & 2.7微调模型
2.6.1 训练和评估数据集
首先,先训练一个线性回归模型:
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
# 模型训练
lin_reg.fit(housing_prepared, housing_labels)![]()
此时就有一个可以工作的线性回归模型了,让我们用几个训练集的实例试试:
# 在几个训练实例上应用完整的预处理
some_data = housing.iloc[:5] # 测试集
some_labels = housing_labels.iloc[:5] # 测试标签
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:", lin_reg.predict(some_data_prepared))
print("Labels:", list(some_labels)) 可以看出,预测的结果还不太准确,第一次预测的失效接近40%。可以使用 Scikit-Learn 的 mean_squared_errod() 函数来测量整个训练集上回归模型的 RMSE ( 均方根误差):
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
# 均方误差
lin_mse = mean_squared_error(housing_labels, housing_predictions)
# 均方根误差
lin_rmse = np.sqrt(lin_mse)
lin_rmse![]()
这太大了...因为大多数区域的median_housing_values都分布在120000~265000美元之间,所以这个结果差强人意。这就是一个典型的模型对训练数据欠拟合的案例,此时通常意味着这些特征可能无法提供足够的信息来供我们做出更好的预测。此时有三个解决方法:
1、选择更加强大的模型;
2、为算法提供更好的特征;
3、减少对模型的限制;
4、...
本模型LinearRegression不是一个正则化模型,所以第三点排除。我们先来看一下一个更为复杂的模型DecisionTreeRegressor是怎么工作的(它能在数据中找到复杂的非线性关系):
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=42)
# 模型训练
tree_reg.fit(housing_prepared, housing_labels)
# 模型预测
housing_predictions = tree_reg.predict(housing_prepared)
# 均方误差
tree_mse = mean_squared_error(housing_labels, housing_predictions)
# 均方根误差
tree_rmse = np.sqrt(tree_mse)
tree_rmse完全没有误差??真的吗??但事实是,这个模型对数据严重过拟合了。如何确认呢?可以使用下面的方式。在有信心启动模型之前,都不要去碰测试集,所以这里需要拿出训练集的一部分用于寻来你,另一部分由于模型验证。
2.6.2 使用交叉验证来更好地评估
评估模型的一种方法是使用 train_test_split 函数将训练集划分为较小的训练集和测试集。还有一种方法是使用 Scikit-Learn 的 K 折交叉验证的功能。比如:它可以将训练集分割成 10 个不同的子集,每个子集称为一个折叠,然后对模型进行 10 训练和评估——每次挑选1个折叠进行评估,使用其他 9 个折叠进行模型训练,返回一个包含 10 次评估分数的数组。
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores)
#交叉验证功能更倾向于使用效用函数(越大越好)而不是成本函数(越小越好)
#所以计算分数的函数实际上是负的MSE函数
def display_scores(temp_scores):
print("Scores:", temp_scores)
print("Mean:", temp_scores.mean())
print("Standard deviation:", temp_scores.std())
display_scores(tree_rmse_scores)误差 71407 ,上下浮动 ±2439。这结果。。怎么比线性模型还糟糕呢?
注意:交叉验证不仅可以得到模型的性能评估值,还可以衡量该评估的精确度(即其标准差)。如果只是用一个验证机,就收不到这里的结果信息。所以,交叉验证的代价就是要多次训练模型,因此也不是一直行得通。保险起见,我们再回头计算一下线性模型的评分:
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores) 最后,我们再来尝试一个模型: RandomForestRegressor 随机森林。它通过特征的随机子集进行多个决策树的训练,然后对其预测取平均。在多个模型的基础上建立模型,这就是集成学习。
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(housing_prepared, housing_labels)#训练
#计算误差
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse这个RMSE的结果看起来不错,但是训练集上的分数还是远低于验证集,这说明该模型仍然存在着过拟合。 解决方法有:简化模型、约束模型(正则化)、获得更多训练数据。不过在此之前,我们应该尝试一边各种机器学习算法的其他模型(具有不同内核的支持向量机,比如神经网络模型)。记住,不要花太多时间调节超参数,我们的目的是筛选几个有效的模型。
每一个尝试过的模型都应该妥善保存,记得同时保存超参数和训练过的参数,以及交叉验证的评分和实际预测的结果,这样便可轻松对比。通过python的pickle模式或者joblib库,可以轻松保存Scikit-Learn模型,这样可以更有效地将大型NumPy数组(可以用pip安装)序列化:
import joblib
joblib.dump(my_model, "my_model.pkl")
#and later...
my_model_loaded = joblib.load("my_model.pkl")2.7.1 网格搜索
一种方法是手动调整超参数,直到找到一组很好的超参数组合。或者,通过使用 Scikit-Learn 的 GridSearchCV 来寻找最佳的超参数组合:你只需要传入要进行实验地超参数是什么,以及需要尝试的值, GridSearchCV 会使用交叉验证来评估超参数值的所有组合。、
下面通过 GridSearchCV 来搜索 RandomForestRegressor 的超参数值的最佳组合。
from sklearn.model_selection import GridSearchCV
param_grid = [
# 首先评估第一个dict中这3×4=12种超参数组合
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
# 然后评估第二个dict中这2×3=6种超参数组合。设置bootstrap=False(默认是True)
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
#网格搜索将探索RandomForestRegressor超参数值的18种组合
forest_reg = RandomForestRegressor(random_state=42)
# 训练5次(使用的是5-折交叉验证),总共训练(12+6)×5=90次
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)完成后,我们获得最佳的参数组合:
查看评分最高的超参数组合:
grid_search.best_params_![]()
被评估的n_estimator最大值是8和30,所以可以试试更高的值以改善评分。由于超参数的最佳值都处于取值范围的右边界,可能需要再扩大取值范围,继续寻找(这一步要等5min):
param_grid = [
{'n_estimators': [30, 50, 70, 90], 'max_features': [7, 8, 9]},
]
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
grid_search.best_params_这个结果合理满意。
接下来看看当前的最佳估算器(输出只显示非默认的参数):
grid_search.best_estimator_GridSearchCV 计算的各种超参数组合的评分:
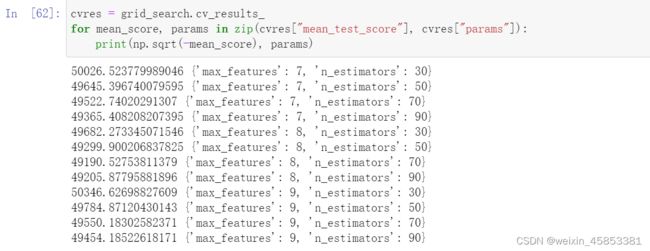
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)根据49682和49190两个评分可以看出,相较于第一次调参结果,第二次的超参数组合确实要高一些。
2.7.2 随机搜索
如果探索的组合数量较少时,网格搜索是一种不错的方法,但当超参数的搜索范围较大时,通常会优先选择使用 RandomizedSearchCV 。它与 GridSearchCV 用法相似,但它不会尝试所有可能的组合,而是在每次迭代中为每个超参数选择一个随机值,然后对一定数量的随机组合进行评估,这种方法有两个显著的好处。
- 如果运行随机
1000个迭代,那么将会探索每个超参数的1000个不同的值(而不像网格搜索方法那样每个超参数仅探索少量几个值)。 - 通过简单地设置迭代次数,可以更好地控制要分配给超参数搜索的计算预算。
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
# 均匀离散随机变量
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=7, high=9),
}
forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
rnd_search.fit(housing_prepared, housing_labels)
看一下 RandomizedSearchCV 计算的各种超参数组合的评分:
cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
结果显而易见,它相比于网格搜索有着更好的随机性,能够在相同时间内探索更多可能的区域,但带来的就是不确定性,就如同上面的结果, max_features 的取值绝大多数为 7 。
2.7.4 分析最佳模型及其误差
通过检查最佳模型,你总是可以得到一些好的洞见,如在进行准确预测的时候, RandomForestRegressor 可以指出每个属性的相对重要程度:
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
将这些重要性分数显示在对应的属性名称旁边:
extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
# cat_encoder: OneHotEncoder()
cat_encoder = full_pipeline.named_transformers_["cat"]
# cat_one_hot_attribs: ['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN']
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)有了这些信息,就可以尝试着删除一些不太有用的特征,如 ocean_proximity 中只有 INLAND 类别是有用的,我们可以试着删除其他所有的类别( <1H OCEAN> 、 NEAR OCEAN 、 NEAR BAY 、 ISLAND )。
2.7.5 通过测试集评估系统
经过前面的训练,现在有了一个表现足够优秀的系统了,是时候用测试集评估最终模型的时候了,我们只需要从测试集中获取预测器和标签,运行 full_pipeline 来转换数据(调用 transform() 而不是 fit_transform() ),然后在测试集上评估最终模型。
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
# 数据处理
X_test_prepared = full_pipeline.transform(X_test)
# 模型预测
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse在某些情况下,泛化误差的这种点估计将不足以说服你启动生产环境:如果它只比当前生产环境中的模型好0.1%呢?为了得到这个估计的准确度,我们可以使用 scipy.stats.t.interval() 计算泛化误差的 95% 置信区间。
from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))
如果之前进行过大量的超参数调整,这时的评估结果往往会略逊于你之前使用交叉验证是的表现结果(通过不断调整,系统在测试集上面终于表现良好,但在未知数据集上可能达不到这么好的效果)。在上面的结果中,结果尽管并非如此,但你也一定不要去继续调整参数,不要试图再努力让测试集的结果变得好看,因为这些改进在泛化到新的数据集时又会变成无用功。