R语言：逆变换法生成随机数

一、概念解释

1、PDF

probability density function 概率密度函数，简称密度函数。连续型随机变量的概率密度函数是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数

借陈希孺老师所著的《概率论与数理统计》中关于概率密度函数的释义以方便理解概念。

2、PMF

probability mass function 概率质量函数, 概率质量函数是离散随机变量在各特定取值上的概率（就是离散型随机变量的分布律）

例如，抛掷硬币，若为正面记X = 1，反面记x = 0，则概率质量函数为:

3、CDF

cumulative distribution function 累积分布函数 ，也叫分布函数，是概率密度函数的积分

常用积分表

二、连续型情况举例

步骤:
1、设U = 概率密度函数积分 = 分布函数
2、分布函数求逆，得到x = 式①
3、构造符合均匀分布的随机数 U = runif(num, start, stop)
4、随机数U代入step2中式①，即可得到对应随机数
5、验证生成的x是否符合预期： 绘制x的频数直方图，绘制总体密度函数曲线

利用逆变换法生成1000个服从$f_x(x)=3x^2,0<x<1$的随机数。

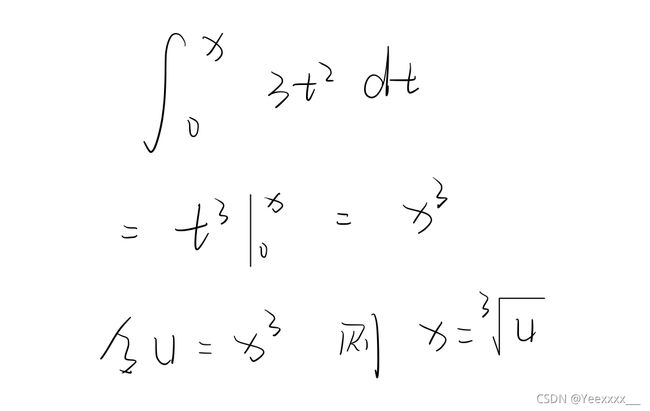
代码实现：

U = runif(1000,0,1)  # 生成1000个服从[0,1]均匀分布的随机数
x = U^(1/3)   # 式① 生成服从题目分布的随机数
hist(x, prob = TRUE)  # 绘制生成随机数x的频数直方图
xx = seq(0,1,0.1)
lines(xx ,3 * xx ^ 2)  # 绘制密度函数，与频数分布直方图的趋势作比较

部分结果展示：

验证结果展示：

练习：
利用逆变换法生成服从$f_x(x)=\frac{x-2}{8},2<x<6$的5000个随机数。

代码实现：

U = runif(5000,0,1)  # 生成1000个服从[0,1]均匀分布的随机数
x = 4*sqrt(U)+2   # 式① 生成服从题目分布的随机数
hist(x, prob = TRUE)  # 绘制生成随机数x的频数直方图
xx = seq(2,6,0.1)
lines(xx ,(xx-2)/8)  # 绘制密度函数，与频数分布直方图的趋势作比较

三、离散型情况举例

离散型生成随机数的四种方法：
① R语言内置函数
② sample函数
③ 逆变换法
④ 接受拒绝法

步骤:
1、对照列联表写分布函数
2、分布函数求逆
3、构造符合均匀分布的随机数 U = runif(num, start, stop)
4、随机数U代入step2中式①，即可得到对应随机数
5、验证生成的x是否符合预期： 制表统计看频率

利用逆变换法生成1000个服从下列概率质量函数的随机数。

X	0	1	2	3	4
P	0.1	0.2	0.2	0.2	0.3

代码实现：

n = 1000
x = seq(0, 4, 1)
p = c(0.1, 0.2, 0.2, 0.2, 0.3)
FF = c(0,cumsum(p)); FF  #累加得到分布函数
y1 = integer(n)  # 逻辑向量
m = length(FF)
u = runif(n)  # 生成1000个服从[0,1]均匀分布的随机数
for(i in 1:m-1){  # u代入逆运算的结果
  ind = u>FF[i] & u<=FF[i+1];  # or = |   and = &
  y1[ind]=x[i];
}; y1
table(y1)/n   # 频数验证

部分结果展示:

验证结果展示: