统计机器学习代码合集

P39 习题应用8

college = read.csv("./data/College.csv",sep = ',',header = TRUE);


rownames(college) = college[,1] # 将第一列令为行名
# fix(college)
college = college[,-1]  # 删除第一列
# fix(college)

college$Private=huaas.factor(college$Private)  # Private是字符型变量 所以因子化

# 数据特征
summary(college)

# 散点图矩阵
pairs(college)

# 箱线图
plot(college$Private, college$Outstate)  # P对O的沿边箱线图
   # 横坐标为P的Yes和NO ，纵坐标为O的数值

Elite = rep("No", nrow(college))  # 创建一个列表Elite，重复赋值college行数个No
Elite[college$Top10perc>50]="Yes"   # 大于50赋值Y 向量运算
Elite = as.factor(Elite)  # 转化为因子
college = data.frame(college, Elite) # 合并
summary(Elite)
plot(college$Elite, college$Outstate)


# 直方图
par(mfrow = c(2,2)) # 窗口分区
hist(college$Accept,breaks = 5, prob=T)
hist(college$Accept,breaks = 10, prob=T)
hist(college$Accept,breaks = 20, prob=T)
hist(college$Accept,breaks = 50, prob=T)

第二次作业

1.人造数据:生成200个f(x)=sinx y=f(x)+ei~N(0,0.2) 生成正态分布随机数rnorm
2.线性回归拟合数据：输出均方误差
3.多项式函数poly（1，3，5，20，23）再拟合点

# 生成sin+噪声数据
set.seed(11)  # 设置随机种子
x = runif(200,-10,10); # 200个-10到10之间均匀分布的随机数
x = sort(x)  # 排序
y = sin(x)+rnorm(200,0,0.2)   # sinx+e,e服从正态分布均值为0，方差为0.2的随机扰动

# 画图
plot(x,y,type = 'l',col = 'red',main = "Ganerate random data")
lines(x,sin(x),col = 'blue')
legend(x = 'bottomleft', 
       legend = c(expression(y == sinx+e), expression(y == sinx)),
       lty =1,
       col = c('red', 'blue'),
       bty = 'n',
       horiz = T,
       cex = 0.8)
       
# 计算mse函数
MSE_fit = function(y,fit,p){
  n=length(fit$residuals)
  rse = sqrt(sum(fit$residuals^2)/(n-p-1)) # https://www.cnblogs.com/HuZihu/p/9692814.html
  mse1 = rse^2*((n-p-1)/n);mse1
}

# 线性回归
fit1 = lm(y~x)
summary(fit1)
MSE_fit(y,fit1,1)  # 计算mse

# 做图对比
plot(x,y,main = "Linear regression",cex = 0.8)
fit1_y = predict(fit1)
lines(x,fit1_y,col ='red')
legend(x = 'bottomleft', 
       legend = c(expression(y == sinx+e), expression('Predicts')),
       lty =1,
       col = c('black', 'red'),
       bty = 'n',
       horiz = T,
       cex = 0.8)

# 多项式绘图图例函数
pr_plot = function(x,y,fit,main_num){
  plot(x,y,main = main_num, cex = 0.8)
  fit_y = predict(fit)
  lines(x,fit_y, col = 'red')
  legend(x = 'bottomleft', 
        legend = c(expression(y == sinx+e), expression('Predicts')),
        lty =1,
        col = c('black', 'red'),
        bty = 'n',
        horiz = T,
        cex = 0.8)
        
# 多项式函数拟合
# 方法一：各画一个图
mse = c()
for(i in seq(3,14)){
  fit = lm(y~poly(x, i))  # 多项式函数
  pr_plot(x,y,fit,paste('Polynomial regression',i))
  mse = c(mse,MSE_fit(fit, i))
}
mse
}

# 方法二：线画在一个图上
mse = c()
plot(x,y)
for(i in seq(3,14)){
  fit = lm(y~poly(x, i))
  mse = c(mse,MSE_fit(fit, i))
  lines(x,predict(fit),col=i)  
}
mse

# Simulated data 生成数据
GenerateDataSin = function(n, sigma1, sigma2)
{
  x = seq(0,2*pi,length.out = n)  # x的范围和输出长度n
  set.seed(1) # 设置随机种子
  r = rnorm(n, mean = 0, sd = sigma1) # x的随机扰动 服从均值为0，方差为sigma1的正态分布
  X = x + r
  set.seed(2)  
  epsilon = rnorm(n, mean = 0, sd = sigma2)  # 随机误差项
  Y = sin(X) + epsilon 
  dataAll = data.frame(X,Y) # x y 合并为数据框
  return(dataAll)  # 返回数据框
}

# Getting training and test data 生成训练集和测试集
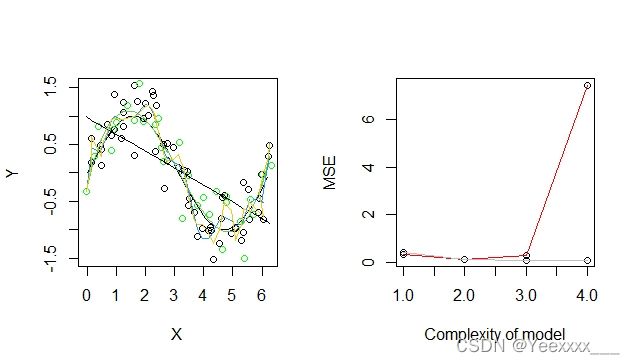
TrainData = GenerateDataSin(60, 0.1, 0.3)  # 训练集
par(mfrow = c(1, 2))
plot(TrainData$X, TrainData$Y, xlab = "X", ylab = "Y")
TestData = GenerateDataSin(30, 0.1, 0.3)  # 测试集
points(TestData$X, TestData$Y,col = "green") # 测试集的点"Green" points represent the test data

# 标准图像绘制
xx = seq(0,2*pi, by = 0.1)   # 0到2pi，间隔为0.1
lines(xx,sin(xx))  # sinx标准图像


# Fitting the model 拟合模型
ModelSin = function(Train, Test, k) # k是多项式的次数
{
  modelfit.lm = lm(Y~poly(X, k), data = Train)  # 线性回归
  trainX = Train$X
  tstX = Test$X
  yhat.train = predict(modelfit.lm, data.frame(X = trainX))  # 训练集上的预测
  yhat.tst = predict(modelfit.lm, data.frame(X = tstX))  # 测试集预测
  lines(trainX, yhat.train, col = k) # 训练集拟合线
  trainMSE = mean((Train$Y - yhat.train)^2)  # 训练mse 训练集均方误差
  tstMSE = mean((Test$Y - yhat.tst)^2)   # 测试集均方误差
  Output = list(yhat.tst,trainMSE,tstMSE)  # 返回测试集预测 训练均方误差 测试均方误差
  return(Output)
}

Output1 = ModelSin(TrainData, TestData, 1) # 一次 简单线性回归
Output3 = ModelSin(TrainData, TestData, 3) # 绿色曲线
Output20 = ModelSin(TrainData, TestData, 20)  # 蓝色
Output23 = ModelSin(TrainData, TestData, 23)  # 黄色

# MSE
TrainMSE = c(Output1[[2]], Output3[[2]], Output20[[2]], Output23[[2]])
TrainMSE  # 训练集均方误差 随光滑度的增大 单调递减
TestMSE = c(Output1[[3]], Output3[[3]], Output20[[3]], Output23[[3]])
TestMSE  # 测试集均方误差 随光滑度增大呈现u形分布
plot(TestMSE,xlab = "Complexity of model", ylab = "MSE")
lines(TestMSE, col = "red")
points(TrainMSE)
lines(TrainMSE, col = "grey")

第三章 简单线性回归

Auto = read.csv("./data/Auto.csv")
for(i in 1:length(Auto[,1])){
  if(Auto$horsepower[i] == "?"){
    Auto$horsepower[i] = NA
  }
}   # 数据中？的处理
Auto = na.omit(Auto)  # 删除空值
class(Auto$horsepower)  # "character"
Auto$horsepower = as.numeric(Auto$horsepower) # 转换类型为数值
attach(Auto)


# lm 简单线性回归 
  # 二者之间是否具有相关关系
cor.test(mpg,horsepower)
  # Pearson's product-moment correlation
  # 
  # data:  mpg and horsepower
  # t = -24.489, df = 390, p-value < 2.2e-16
  # alternative hypothesis: true correlation is not equal to 0
  # 95 percent confidence interval:
  #  -0.8146631 -0.7361359
  # sample estimates:
  #        cor 
  # -0.7784268 
    # 从相关系数上判断，mpg与horsepower具有高度负相关关系，相关系数高达0.778
    # 进一步地可以相关性显著性检验，
    # H0为X和Y之间没有相关关系，p值远小于0.05，拒绝原假设，二者之间一定有关系。
    
fit1 = lm(mpg~horsepower) # 拟合简单线性回归模型 
summary(fit1)  # 详细信息
coef(fit1)  # 参数
  # 模型写为方程形式 ：mpg = 39.9358610 - 0.1578447 * horsepower 
# 当horsepower=98时的预测值为?
a = as.data.frame(98)
colnames(a)=list("horsepower") 
predict(fit1,a)  # 24.46708 
# 当horsepower=98时 对应的置信区间为？[23.97308 24.96108]
predict(fit1,a,interval = "confidence")
  #      fit      lwr      upr
  # 1 24.46708 23.97308 24.96108
  #     预测值 置信区间下限/上限
# 当horsepower=98时 对应的预测区间为？[14.8094 34.12476]
predict(fit1,a, interval = "prediction")
  #      fit     lwr      upr
  # 1 24.46708 14.8094 34.12476

# 绘制响应变量和预测变量的关系图，用abline()函数显示最小二乘回归线
plot(horsepower,mpg,col="red") 
abline(fit1,col="blue",lw=2)

# 回归诊断图
par(mfrow = c(2, 2))
plot(fit1)
	# Residuals vs Fitted：残差与估计值之间的关系，数据点应该大致落在两倍标准差也就是2、-2之			间，且这些点不应该呈现任何有规律的趋势.
	# Normal QQ：若满足正态假设，那么图上的点应该落在呈45度角的直线上；若不是如此，那么就违反了正态性的假设.
	# Scale-Location：GM假设中的同方差可以通过这张图诊断，方差应该呈现基本确定或持平的样子.
	# Cook’s distance：Cook距离，用于强影响点的诊断.

Auto$name = as.factor(name) # 转化为因子
pairs(Auto)  # 绘制矩阵散点图
# 计算变量之间的相关系数矩阵，排除定性变量name
cor(Auto[,1:8])
  
  # 多元线性回归
fit2 = lm(mpg~.-name,data = Auto) 
summary(fit2)
  #（1）由F统计量值为254.4可知，远大于 1，且 F 统计量的 p 值几乎为零。 说明至少一个预测变量与响应变量有关系。
  #（2）由模型信息可知，预测变量displacement、weight、year、origin的 p 值较小，与响应变量具有显著关系。 
  #（3）year 的系数为正值，说明随着车龄增长，油耗会增加。增加一年车龄，每桶油可行驶公里数平均增加0.7508公里
par(mfrow=c(2,2)) 
plot(fit2)

  # 有交互项的线性回归模型拟合
fit3 = lm(mpg~.-name+horsepower*cylinders,data=Auto) 
summary(fit3)
  # 存在统计显著的交互项，不过系数较小。
  
  # 非线性变换
fit4 = lm(mpg ~ .-name + log(horsepower), data=Auto)
summary(fit4)
  # horsepower 的对数项 p 值几乎为 0，说明部分预测变量与响应变量之间有非线性关系。

fit5 = lm(mpg ~ .-name + sqrt(horsepower), data=Auto) # 开根
summary(fit5)

第五章 重抽样方法

### (a)生成一个模拟数据集如下：
set.seed(1)
y=rnorm(100)
x=rnorm(100)
y=x-2*x^2+rnorm(100)
	# n = 100, p = 2. 
	# 模型形式为 $Y=X−2X^2+ϵ$.

### (b)做X对Y的散点图
plot(x, y)

### (c)LOOCV误差
library(boot)
data = data.frame(x, y)  # 定义数据框
	# 函数：留一法拟合+返回误差
Loocv_fit = function(seed,po){  # po（poly）
  set.seed(seed)
  glm.fit = glm(y ~ poly(x, po))  # 拟合模型  glm和lm一样，只是glm可以和cv.glm一起用
  cv.err = cv.glm(data, glm.fit) # 第一个参数为数据 第二个参数是模型
  return(cv.err$delta)  # 交叉验证的结果：原始结果 和调整后的结果
}

for(i in 1:4){
  print(i)
  print(Loocv_fit(11,i)) # 11是随机种子
}
# 用交叉验证选出的模型是二次的

### (d) 变换随机种子
for(i in 1:4){
  print(i)
  print(Loocv_fit(12,i))
}
#结果并没有变化，因为LOOCV在训练集与验证集上的分割并不存在随机性，所以总会得到相同的结果

### （e）
# ii. $Y= \beta_{0} + \beta_{1}X + \beta_{2}X^2 + ϵ$ 有最小的LOOCV误差，跟预计结果一致，因为（a）中生成随机数的的模型形式就是二次的，说明我们能够通过LOOCV选出一个较好的模型.

### （f）看t检验选出来的特征与交叉验证的结果是否吻合
fit = glm(y ~ poly(x, 4))
summary(fit)
# 一致，一次项和二次项的p值小于0.05，显著具有统计意义，三次四次不显著。统计检验的结果与LOOCV结果一致。

# P182 8 abcd
### (a)生成x 和 $\epsilon$ 
set.seed(1) # 设置随机种子
X = rnorm(100)
eps = rnorm(100)

### (b) 建立模型，生成响应变量Y
beta0 = 1
beta1 = 3
beta2 = -2
beta3 = 0.5
Y = beta0 + beta1 * X + beta2 * X^2 + beta3 * X^3 + eps

library(leaps)
data = data.frame(y = Y, x = X)  # 构造同时包含X和Y的数据集、框
regfit.full = regsubsets(y ~ poly(x, 10, raw = T), data = data, nvmax = 10)  # ?raw 最优子集选择法 nvmax是最多选择的特征个数
mod.summary = summary(regfit.full)
mod.summary

# 通过cp、bic、adjust R^2判断选择哪一个模型最优，cp bic最小，adjustR^2最大
which.min(mod.summary$cp)
which.min(mod.summary$bic)
which.max(mod.summary$adjr2)
	#cp、bic最小，adjust $R^2$最大的都是3

# 可视化cp
par(mfrow = c(1,2))
plot(mod.summary$cp, ylab = "Cp",type = "l")  # 十个模型的cp的折线图
points(3, mod.summary$cp[3],col = "red", lwd = 2)
plot(regfit.full,scale = 'Cp') 
# 可视化bic
par(mfrow = c(1,2))
plot(mod.summary$bic, ylab = "BIC",type = "l")
points(3, mod.summary$bic[3],col = "red", lwd = 2)
plot(regfit.full,scale = 'bic')
# 可视化adjr2
par(mfrow = c(1,2))
plot(mod.summary$adjr2, ylab = "Adjusted R2",type = "l")
points(3, mod.summary$adjr2[3],col = "red", lwd = 2)
plot(regfit.full,scale = 'adjr2')

# 拟合三次模型
b_fit=lm(y ~ poly(x,3, raw = T), data = data) 
summary(b_fit)
coef(b_fit)  # 最优模型的估计系数  真实系数是 1 3 -2 0.5


### (d)向前向后逐步
mod.fwd = regsubsets(y ~ poly(x, 10, raw = T), data = data, nvmax = 10, 
    method = "forward") # 向前
mod.bwd = regsubsets(y ~ poly(x, 10, raw = T), data = data, nvmax = 10, 
    method = "backward")  # 向后
fwd.summary = summary(mod.fwd)
bwd.summary = summary(mod.bwd)

which.min(fwd.summary$cp)
which.min(fwd.summary$bic)
which.max(fwd.summary$adjr2)

which.min(bwd.summary$cp)
which.min(bwd.summary$bic)
which.max(bwd.summary$adjr2)

# 与（c）中最优子集选择的结果一致，均为3次，由于本次实验p并不大，最优子集选择法仍适用，向前向后逐步也得到一致的结果，暂且说明向前向后逐步选择法还是很优秀的，运算效率高，也比较准确。