自编码器
自编码器是一种基于无监督学习的数据维度压缩和特征表达方法。多层自编码器能够更好地进行压缩及特征表达。本部分介绍自编码器及其变种,如降噪自编码器、稀疏自编码器,以及由多层自编码器组成的栈式自编码器.
自编码器
自编码器 ( autoencoder ) (\text{autoencoder}) (autoencoder)是一种有效的数据维度压缩算法,主要应用在以下两个方面
- 构建一种能够重构输入样本并进行特征表达的神经网络
- 训练多层神经网络时,通过自编码器训练样本得到参数初始值
第一条中的特征表达是指对于分类会发生变动的不稳定模式,例如手写字符识别中由于不同人的书写习惯和风格的不同造成字符模式不稳定,或者输入样本中包含噪声等情况,神经网络也能将其转换成可以准确识别的特征。当样本中包含噪声时,如果神经网络能够消除噪声,则被称为降噪自编码器 ( denosing autoencoder ) (\text{denosing autoencoder}) (denosing autoencoder)的网络,它在自编码器中引入了正则化项,以去除冗余信息。
第二条中的得到参数初始值是指在多层神经网络中得到最优参数。一个多层神经网络的训练,首先要利用随机数初始化训练样本的参数,然后通过训练样本得到最优参数。但是,如果是层数较多的神经网络,即使使用误差反向传播算法也很难把误差梯度有效反馈到底层,这样就会导致神经网络训练困难。所以,需要使用自编码器计算每层的参数,并将其作为神经网络的参数初始值逐层训练,以便得到更加完善的神经网络模型。首先,我们来看一下自编码器
自编码器的基本形式如上图所示,和受限玻尔兹曼机一样,都是两层结构,由输入层和输出层组成。图中的输入数据 x \boldsymbol x x与对应的连接权重 W \boldsymbol W W相乘,再加上偏置 b \boldsymbol b b,并经过激活函数 f ( ⋅ ) \boldsymbol{f(\cdot)} f(⋅)变换后,就可以得到输出 y \boldsymbol y y,如下所示。 y = f ( W x + b ) ( 1 ) \boldsymbol{y=f(W x+b)} \qquad(1) y=f(Wx+b)(1)自编码器是一种基于无监督学习的神经网络,目的在于通过不断调整参数,重构经过维度压缩的输入样本。现在我们来看一种能够重构输入样本的三层神经网络。
我们把输入层到中间层之间的映射称为编码,把中间层到输出层之间的映射称为解码。编码和解码的过程如图所示,先通过编码得到压缩后的向量,再通过解码进行重构。
中间层和重构层之间的连接权重及偏置分别记作 W ~ \boldsymbol{\widetilde{W}} W 和 b ~ \boldsymbol{\widetilde{b}} b ,重构值(解码结果)记作 x ~ \widetilde{\boldsymbol{x}} x x ~ = f ~ ( W ~ y + b ~ ) ( 2 ) \boldsymbol{\tilde{x}=\widetilde{f}(\widetilde{W} y+\tilde{b})} \qquad(2) x~=f (W y+b~)(2)
这里, f ( ⋅ ) \boldsymbol{f(\cdot)} f(⋅)表示编码器的激活函数, f ~ ( ⋅ ) \boldsymbol{\widetilde{f}(\cdot)} f (⋅)表示解码器的激活函数。
根据公式 ( 1 ) (1) (1)和公式 ( 2 ) (2) (2)可以得到重构层的 x ~ \widetilde{\boldsymbol{x}} x x ~ = f ~ ( W ~ f ( W x + b ) + b ~ ) ( 3 ) \boldsymbol{\tilde{x}=\widetilde{f}(\widetilde{W} f(W x+b)+\tilde{b})} \qquad(3) x~=f (W f(Wx+b)+b~)(3)
自编码器的训练就是确定编码器和解码器的参数 W , W ~ , b , b ~ \boldsymbol{W, \widetilde{W}, b, \tilde{b}} W,W ,b,b~的过程。首先,使用公式 ( 3 ) (3) (3)计算输入样本 x \boldsymbol{x} x的重构值 x ~ \widetilde{\boldsymbol{x}} x ,然后使用误差反向传播算法调整参数值,不断迭代上述过程直至误差函数收敛于极小值。误差函数 E E E可以使用公式 ( 4 ) (4) (4)中的最小二乘误差函数或公式 ( 5 ) (5) (5)中的交叉熵代价函数。 E = ∑ n = 1 N ∥ x n − x n ~ ∥ 2 ( 4 ) E=\sum_{n=1}^{N}\left\|x_{n}-\widetilde{x_{n}}\right\|^{2} \qquad(4) E=n=1∑N∥xn−xn ∥2(4) E = − ∑ i = 1 N ( x i log x ~ i + ( 1 − x i ) log ( 1 − x ~ i ) ) ( 5 ) E=-\sum_{i=1}^{N}\left(x_{i} \log \tilde{x}_{i}+\left(1-x_{i}\right) \log \left(1-\tilde{x}_{i}\right)\right)\qquad(5) E=−i=1∑N(xilogx~i+(1−xi)log(1−x~i))(5)
上面公式中的 x i x_{i} xi和 x ~ i \tilde{x}_{i} x~i分别表示 x x x和 x ~ \tilde{x} x~的第 i i i个元素。
前面介绍了编码器的连接权重 W \boldsymbol{W} W和解码器的连接权重 W ~ \boldsymbol{\widetilde{W}} W ,两者数值不同。不过编码器和解码器可以共享连接权重,这称为权值共享,可以用如下公式表示: W ~ = W ( 6 ) \boldsymbol{\widetilde{W}={W}} \qquad(6) W =W(6)自编码器和受限玻尔兹曼机的结构相似,都是两层。两者最大的区别在于受限玻尔兹曼机是一个概率模型,训练目的是求出能够使似然函数达到极大值的参数估计,而且正向传播时,我们可以以似然函数的值为概率决定单元的输出结果。而自编码器需要定义一个误差函数,通过调整参数使得输入样本和重构结果的误差收敛于极小值。和神经网络一样,自编码器的计算结果也会进行正向传播,这就是自编码器和受限玻尔兹曼机的主要区别。
降噪自编码器
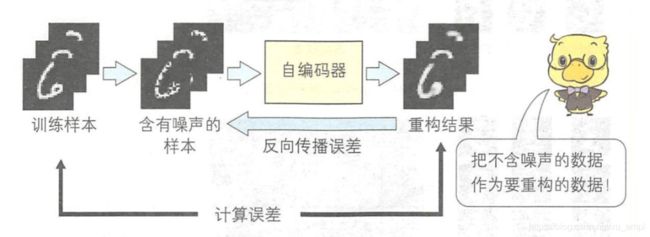
自编码器的重构结果和输入模式是相同的。在自编码器的基础上衍生的降噪自编码器如下图所示。
降噪自编码器的网络结构与自编码器一样,只是对训练方法进行了改进,改进后的训练过程如下图所示:
自编码器是把训练样本直接输入给输入层,而降噪自编码器则是把通过向训练样本中加入随机噪声得到的样本 x ~ \tilde{\boldsymbol{x}} x~输入给输入层。 x ~ = x + v x \tilde{x}=x+v x x~=x+vx 随机噪声 v v v服从均值为 0 0 0、方差为 σ 2 \sigma^{2} σ2的正态分布。我们需要训练神经网络,使得重构结果与不含噪声的样本之间的误差收敛小于极小值。误差函数会对不含噪声的输入样本进行测试,故降噪自编码器能够完成下述两项训练。
- 保持输入样本不变的条件下,提取能够更好地反映样本属性的特征
- 消除输入样本中包含的噪声
稀疏自编码器
自编码器是一种有效的数据维度压缩算法,它会对神经网络的参数进行训练,使输出层可能如实地重构输入样本。但是中间层的单元个数太少会导致神经网络很难重构输入样本,而单元个数太多又会产生单元冗余,降低压缩效率。为了解决这个问题,人们将稀疏正则化引入到自编码器中,提出了稀疏自编码器。通过增加正则化项,大部分的输出都变为了 0 0 0,这样就能利用少数单元有效完成压缩或重构。加入正则化项后的误差函数 E E E如下所示。 E = ∑ n = 1 N ∥ x n − x ~ n ∥ 2 + β ∑ j = 1 M K L ( ρ ∥ ρ ^ j ) E=\sum_{n=1}^{N}\left\|x_{n}-\tilde{x}_{n}\right\|^{2}+\beta \sum_{j=1}^{M} K L\left(\rho \| \hat{\rho}_{j}\right) E=n=1∑N∥xn−x~n∥2+βj=1∑MKL(ρ∥ρ^j) ρ ^ j \hat{\rho}_{j} ρ^j表示中间层第 j j j个单元的平均激活度。 ρ ^ j = 1 N ∑ n = 1 N f ( W j x n + b j ) \hat{\rho}_{j}=\frac{1}{N} \sum_{n=1}^{N} f\left(W_{j} x_{n}+b_{j}\right) ρ^j=N1n=1∑Nf(Wjxn+bj) K L ( ρ ∥ ρ ^ j ) K L\left(\rho \| \hat{\rho}_{j}\right) KL(ρ∥ρ^j)表示 K L KL KL距离 K L ( ρ ∥ ρ ^ j ) = ρ log ( ρ ρ ^ j ) + ( 1 − ρ ) log ( 1 − ρ 1 − ρ ^ j ) K L\left(\rho \| \hat{\rho}_{j}\right)=\rho \log \left(\frac{\rho}{\hat{\rho}_{j}}\right)+(1-\rho) \log \left(\frac{1-\rho}{1-\hat{\rho}_{j}}\right) KL(ρ∥ρ^j)=ρlog(ρ^jρ)+(1−ρ)log(1−ρ^j1−ρ)
这里的 ρ {\rho} ρ表示平均激活度的目标值, ρ ^ j \hat{\rho}_{j} ρ^j表示计算得到的平均激活度和目标值的差异。 ρ {\rho} ρ值越接近于0,中间层的平均激活地 ρ ^ j \hat{\rho}_{j} ρ^j就越小。连接权重 W j W_j Wj和偏置 b j b_j bj需要不断调整,以使误差函数 E E E收敛于极小值。 β \beta β是在原来的误差函数的基础上增加的参数,用于控制稀疏性的权重。在训练网络时,需要通过不断调整参数使 β \beta β达到极小值,稀疏编码器的训练也需要使用误差反向传播算法,通过对误差函数求导计算输入层和中间层,以及中间层和重构层之间的连接权重 W j W_j Wj和偏置 b j b_j bj的调整值。在对误差函数 E E E进行求导时必须考虑 K L ( ρ ∥ ρ ^ j ) K L\left(\rho \| \hat{\rho}_{j}\right) KL(ρ∥ρ^j)的导数。 ∂ ∂ u j ( β ∑ j = 1 M K L ( ρ ∥ ρ ^ j ) ) = β ∂ ∂ ρ ^ j K L ( ρ ∥ ρ ^ j ) ∂ ρ ^ j ∂ u j = ( − ρ ρ ^ j + 1 − ρ 1 − ρ ^ j ) ∂ ρ ^ j ∂ u j \begin{aligned} \frac{\partial}{\partial u_{j}}\left(\beta \sum_{j=1}^{M} K L\left(\rho \| \hat{\rho}_{j}\right)\right) &=\beta \frac{\partial}{\partial \hat{\rho}_{j}} K L\left(\rho \| \hat{\rho}_{j}\right) \frac{\partial \hat{\rho}_{j}}{\partial u_{j}} \\ &=\left(-\frac{\rho}{\hat{\rho}_{j}}+\frac{1-\rho}{1-\hat{\rho}_{j}}\right) \frac{\partial \hat{\rho}_{j}}{\partial u_{j}} \end{aligned} ∂uj∂(βj=1∑MKL(ρ∥ρ^j))=β∂ρ^j∂KL(ρ∥ρ^j)∂uj∂ρ^j=(−ρ^jρ+1−ρ^j1−ρ)∂uj∂ρ^j由 ρ ^ j = 1 N ∑ n = 1 N f ( W j x n + b j ) \hat{\rho}_{j}=\frac{1}{N} \sum_{n=1}^{N} f\left(W_{j} x_{n}+b_{j}\right) ρ^j=N1∑n=1Nf(Wjxn+bj)有下式 ∂ ∂ u j ( β ∑ j = 1 M K L ( ρ ∥ ρ ^ j ) ) = ( − ρ ρ ^ j + 1 − ρ 1 − ρ ^ j ) ∂ ρ ^ j ∂ u j f ′ ( W j x n + b j ) \frac{\partial}{\partial u_{j}}\left(\beta \sum_{j=1}^{M} K L\left(\rho \| \hat{\rho}_{j}\right)\right)=\left(-\frac{\rho}{\hat{\rho}_{j}}+\frac{1-\rho}{1-\hat{\rho}_{j}}\right) \frac{\partial \hat{\rho}_{j}}{\partial u_{j}} f^{\prime}\left(W_{j} x_{n}+b_{j}\right) ∂uj∂(βj=1∑MKL(ρ∥ρ^j))=(−ρ^jρ+1−ρ^j1−ρ)∂uj∂ρ^jf′(Wjxn+bj)
平均激活度是根据所有样本计算出来的,所以在计算任何单元的反向传播之前,需要对所有样本计算一遍正向传播,从而获取平均激活度。所以使用小批量梯度下降法进行训练时的效率很低,要想解决这个问题,可以只计算 Mini-Batch \text { Mini-Batch } Mini-Batch 中包含的训练样本的平均激活度,然后在 Mini-Batch \text { Mini-Batch } Mini-Batch 之间计算加权平均并求近似值。假设时刻 t − 1 t-1 t−1的 Mini-Batch \text { Mini-Batch } Mini-Batch 的平均激活度为 ρ ^ j t − 1 \hat{\rho}_{j}^{t-1} ρ^jt−1,当前时刻 t t t的 Mini-Batch \text { Mini-Batch } Mini-Batch 的平均激活度为 ρ ^ j t \hat{\rho}_{j}^{t} ρ^jt,则有下式成立 ρ ^ j ( t ) = λ ρ ^ j ( t − 1 ) + ( 1 − λ ) ρ ^ j ( t ) \hat{\rho}_{j}^{(t)}=\lambda \hat{\rho}_{j}^{(t-1)}+(1-\lambda) \hat{\rho}_{j}^{(t)} ρ^j(t)=λρ^j(t−1)+(1−λ)ρ^j(t)这里的 λ \lambda λ是权重。 λ \lambda λ越大,则时刻 t − 1 t-1 t−1的 Mini-Batch \text { Mini-Batch } Mini-Batch 所占的比重也越高。
栈式自编码器
自编码器、降噪编码器以及稀疏编码器都是包含编码器和解码器的三层结构,但是在进行维度压缩时,可以只包括输入层和中间层。把输入层和中间层多层堆叠后,就可以得到栈式自编码器。栈式自编码器和深度信念网络一样,都是逐层训练,从第二层开始,前一个自编码器的输出作为后一个自编码器的输入,但两种网络的训练方法不同。深度信念网络是利用对比散度算法逐层训练两层之间的参数。而栈式自编码器的训练则如下图所示
首先训练一个自编码器,然后保留第一个自编码器的编码部分,并把第一个自编码器的中间层作为第二个自编码器的输入层进行训练,后续过程就是反复地把前一个自编码器的中间层作为后一编码器的输入层,进行迭代训练。通过多层堆叠,栈式自编码器能够有效地完成输入模式的压缩。
《图解深度学习》 山下隆义著 张弥译