离散傅里叶变换(DFT)

离散傅里叶变换(DFT)

原理

对一张图像使用傅里叶变换就是将它分解成正弦和余弦两部分，也就是将图像从空间域(spatial domain)转换到频域(frequency domain)。这一转换的理论基础来自于以下事实：任一函数都可以表示成无数个正弦和余弦函数的和的形式。傅里叶变换就是一个用来将函数分解的工具。
二维图像的傅里叶变换可以用以下数学公式表达：

式中f(i, j)是图像空间域的值而F是频域的值。傅里叶转换的结果是复数，这也显示出了傅里叶变换是一副实数图像（real image）和虚数图像（complex image）叠加或者是幅度图像（magitude image）和相位图像（phase image）叠加的结果。

在实际的图像处理算法中仅有幅度图像（magnitude image）图像能够用到，因为幅度图像包含了我们所需要的所有图像几何结构的信息。但是，如果想通过修改幅度图像或者相位图像来间接修改原空间图像，需要保留幅度图像和相位图像来进行傅里叶逆变换，得到修改后图像。

对于数字图像这种离散的信号，频率大小表示信号变化的剧烈程度或者说是信号变化的快慢。频率越大，变化越剧烈，频率越小，信号越平缓。 对应到图像中，高频信号往往是图像中的边缘信号和噪声信号，而低频信号包含图像变化频繁的图像轮廓及背景等信号。

对于一幅大小为M x N的图像，图像的傅里叶频谱关于(M/2, N/2)的对称性。

• 频谱图A区与D区关于(M/2, N/2)对称
• 频谱图B区和C区关于(M/2, N/2)对称

实现

cv2.dft(src, dst=None, flag=None, nonzeroRows=0)

作用：进行傅里叶变换
src：输入图像
dst：输出图像
flag：转换标识符

• DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换

• DFT_SCALE: 缩放比例标识符，根据数据元素个数平均求出其缩放结果，如有N个元素，则输出结果以1/N缩放输出，常与DFT_INVERSE搭配使用。

• DFT_ROWS: 对输入矩阵的每行进行正向或反向的傅里叶变换；此标识符可在处理多种适量的的时候用于减小资源的开销，这些处理常常是三维或高维变换等复杂操作。

• DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换，这样的结果虽然是复数阵列，但拥有复数的共轭对称性（CCS），可以以一个和原数组尺寸大小相同的实数数组进行填充，这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组（像简单光谱分析等等），通过设置标志位可以使函数生成一个全尺寸的复数输出数组。

• DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换，这样的结果通常是一个尺寸相同的复数矩阵，但是如果输入矩阵有复数的共轭对称性（比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果），便会输出实数矩阵。

nonzeroRows：当参数不为0，函数会假设只有输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值。这样的话函数就可以对其他的行进行更高效的处理节省一些时间，这项技术尤其是在采用DFT计算矩阵卷积时非常有效。

np.fft.fftshift(img)

作用：将图像中的低频部分移动到图像的中心
img：图像

cv2.magnitude(x, y)

作用：计算二维矢量的幅值
x：表示浮点型X坐标值，即实部
y：表示浮点型y坐标值，即虚部
计算方法：

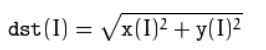
python代码

import cv2   
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread("D:/Study/digital image processing/test/Lena.bmp",0)

# np.float32()将图像数据转换成float32 然后进行傅里叶变换cv2.dft()
dft = cv2.dft(np.float32(img),flags=cv2.DFT_COMPLEX_OUTPUT)
# 将低频信息转换至图像中心
dft_shift = np.fft.fftshift(dft)
# 傅里叶变换后的数据是由实部和虚部构成的，需要进行转换成图像格式才能显示(0,255)
# cv2.magnitude()将实部和虚部转换为实部，乘以20将结果放大
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.title('Input'),plt.xticks([]),plt.yticks([])
plt.subplot(122)
plt.imshow(magnitude_spectrum,cmap='gray')
plt.title('Output'),plt.xticks([]),plt.yticks([])
plt.show()

• 安装的时候是 opencv_python，但在导入的时候采用 import cv2。

• 为OpenCV依赖一些库，可以在本博客中查找一些依赖库的安装方法，例如安装Numpy

• import numpy as np后面的as的意思就是在导入后为了编写程序方便，给numpy起了个别名哦，所以在程序中直接写np就是指的numpy哦！

• cv2.imread(filepath,flags) 读入一张图像

  filepath：要读入图片的完整路径

  flags：读入图片的标志

• matplotlib.pyplot python数据可视化的库

• plt.subplot(nrows,ncols,plot_number),在全局绘图区域中创建一个子绘图区域

• plt.show() 显示创建的绘图对象

• plt.title() 标题的设置

效果展示

从频谱图上可以看出，当将频谱移频到原点以后，图像中心比较亮。在频谱图中，一个点的亮暗主要与这个频率中点的数目和点的灰度值有关，也就是说在空间域中包含这种频率的点越多。而经过频移后，频率为0的部分，也就是傅里叶变换所得到的常量分量在图像中心，往外扩散，点所代表的频率越来越高。也说明了图像中的“能量”主要集中在低频部分。

意义

• 图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。（灰度变化得快频率就高，灰度变化得慢频率就低）。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义，设f是一个能量有限的模拟信号，则其傅立叶变换就表示f的谱。从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅立叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数

  • 傅立叶变换以前，图像（未压缩的位图）是由对在连续空间（现实空间）上的采样得到一系列点的集合，我们习惯用一个二维矩阵表示空间上各点，则图像可由z=f(x,y)来表示。由于空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就由梯度来表示，这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度？因为实际上对图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点，实际上图像上某一点与邻域点灰度值差异的强弱，即梯度的大小，也即该点的频率的大小（差异/梯度越大，频率越高，能量越低，在频谱图上就越 暗。差异/梯度越小，频率越低，能量越高，在频谱图上就越 亮。换句话说，频率谱上越亮能量越高，频率越低，图像差异越小/平缓）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。频谱图，也叫功率图
    

  在经过频谱中心化后的频谱中，中间最亮的点是最低频率，属于直流分量（DC分量）(当频率为0时，表示直流信号，没有变化。在原点(u,v两个频率域变量均为零)的傅里叶变换即等于图像的平均灰度级,F(0，0)称做频 率谱的直流成分)。越往边外走，频率越高。所以，频谱图中的四个角和X,Y轴的尽头都是高频，如下图：
  

我们首先就可以看出，图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外，还有一个好处，它可以分离出有周期性规律的干扰信号，比如正弦干扰，一副带有正弦干扰，移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心，对称分布的亮点集合，这个集合就是干扰噪音产生的，这时可以很直观的通过在该位置放置带阻滤波器消除干扰

参考资料

库的介绍
open cv 介绍：https://blog.csdn.net/qq_41185868/article/details/79675875
Matplotlib的官方文档：https://matplotlib.org/stable/users/index.html
Matplotlib的 imshow使用方法：https://blog.csdn.net/s294878304/article/details/103190322

离散傅里叶变换理论
https://blog.csdn.net/qq_33208851/article/details/94834614
https://blog.csdn.net/Seven_WWW/article/details/107958100