机器学习算法（一）：逻辑回归（Logistic Regression）

背景：逻辑回归可以说是机器学习领域最常用也最经典的模型。

问题：

（1）逻辑回归相比于线性回归有何异同？

异：

逻辑回归处理分类问题，而线性回归处理回归问题。（本质区别）

逻辑回归中，因变量的取值是一个二元分布，模型学习得到的是,即给定自变量和超参数后，得到因变量的期望，并基于这个期望来处理预测和分类问题。

线性回归中，实际求解的是,是对我们假设的真是关系的一个近似，其中

代表的是误差项，使用这个近似来处理回归问题。

        分类和回归是如今机器学习中两个不同的任务，而属于分类算法的逻辑回归，它的命名有一定的历史原因。这个方法是由统计学家David Cox在他1958年的论文《二元序列中的回归分析》（The regression analysis of binary sequences）中提出来的，当年人对于回归与分类的定义与今天是有一定区别的，只是将“回归”这一名字沿用了。实际上，将逻辑回归的公式进行整理，得到其中p=p(y=1|x),也就是将给定输入x预测为正例样本的概率。如果把一个事件的几率（odds）定义为改事件发生的概率与不发生的概率的比值,那么逻辑回归就可以看作是

“y=1|x”这件事情的对数几率的线性回归，于是“逻辑回归”这一称谓也就延续下来了。

           在关于逻辑回归的讨论中，我们均认为y是因变量，而并非，这便引出了逻辑回归与线性回归的最大区别，即逻辑回归的因变量是离散的，而线性回归中的因变量是连续的。  并且在自变量x与确定的前提下，逻辑回归可以看作是广义的线性回归，在因变量y服从二元分布时的一个特殊情况；而使用最小二乘法求解线性回归时，我们认为因变量y服从正态分布。

逻辑回归的定义：数据服从伯努利分布的前提下，使用极大似然估计，利用梯度下降求解参数。

 同：

        二者都使用了极大似然估计对训练样本进行建模。

（线性回归使用最小二乘法，实际就是自变量x与确定，因变量y服从正态分布的假设下，使用极大似然估计的化简：而逻辑回归中通过对似然函数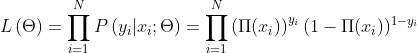的学习，得到最佳的参数。另外，二者在求解超参数的过程中，都使用了梯度下降的方法，这也是监督学习中一个常见相似处之一。

（2）当逻辑回归处理多标签的分类任务时，有哪些常见做法，分别应用于哪些场景，他们之间又有什么样的关系？

使用那种办法来处理多分类问题取决于具体问题的定义。

首先，如果一个样本只对应一个标签，我们假设每个样本属于不同标签的概率服从于几何分布，使用多项逻辑回归（softmax Regression）来进行分类

  

其中为模型参数，而可以看作是对概率的归一化。为了方便起见，我们将{}这K个向量按顺序排列形成n*k维的矩阵，写作，表示整个参数集。一般来说，多项逻辑回归具有参数冗余的特点，即将同时加减一个向量后预测结果不变。

特别的 当类别数为2时，

利用参数冗余的特点，我们将所有的参数都减去，上式变为

其中 而整理后的式子与逻辑回归一致。因此，多项式回归实际上是一个二分类逻辑回归在多标签下的一种拓展。

        当存在样本可能属于多个标签的情况时，我们可以训练K个二分类的逻辑回归分类器。第i个分类器以区分每个样本是否可以归为i类，训练该分类器时，需要把标签重新整理为“第i个标签”与“非第i类标签”两类。通过这样的办法，就可以解决了每个样本可能拥有多个标签的情况。

参考文献：

[1] 百面机器学习：算法工程师带你去面试／诸葛越主 编，葫芦娃著 北京：人民邮电出版社， 2018 ISBN 978 7-115-48736-0